
Wer ich bin
Ich heiße Dmitry Ivanov. Ich bin ein Doktorand der Wirtschaftswissenschaften im zweiten Jahr an der HSE in St. Petersburg. Ich arbeite in der Forschungsgruppe " Agentensysteme und Reinforcement Learning " bei JetBrains Research sowie im internationalen Labor für Spieltheorie und Entscheidungsfindung an der Higher School of Economics . Neben dem PU-Lernen interessiere ich mich für das verstärkte Lernen und Forschen an der Schnittstelle von maschinellem Lernen und Wirtschaft.
Präambel
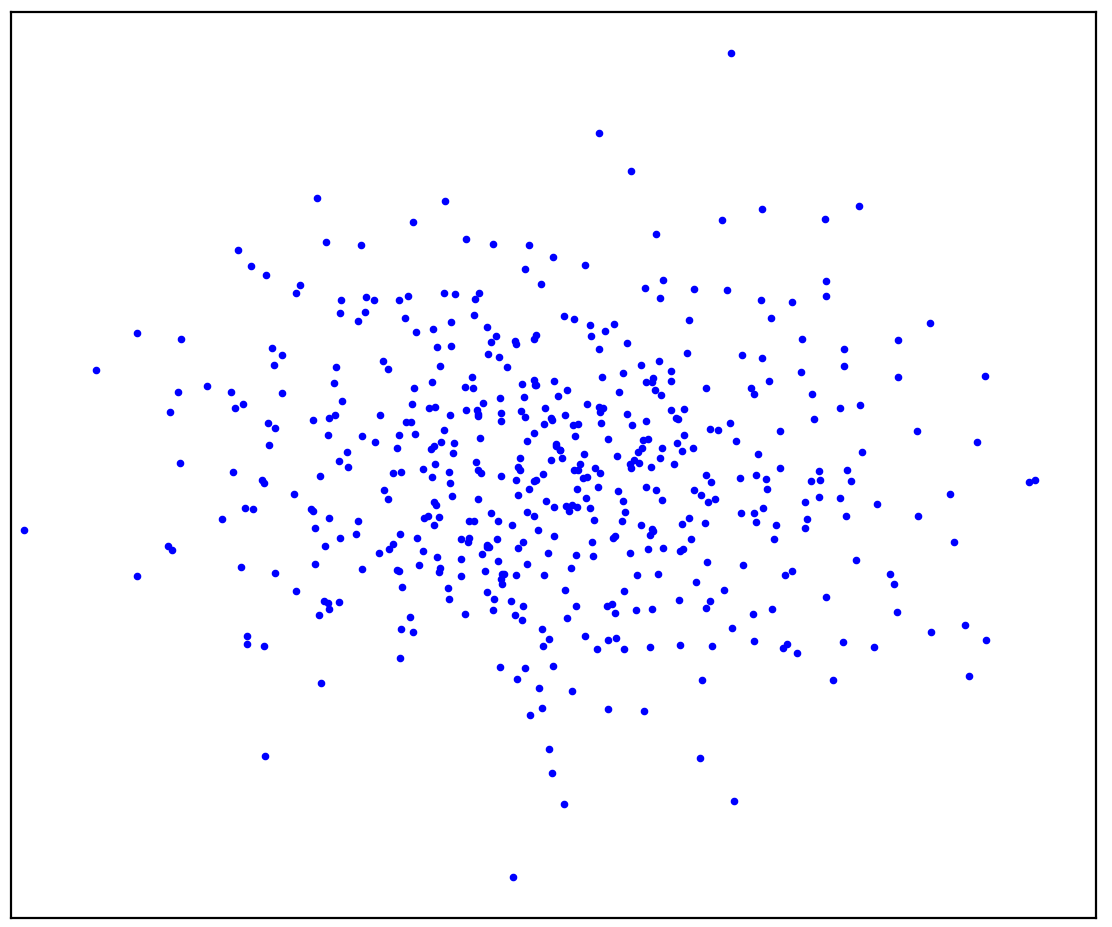
Zahl: 1a. Positive Daten
Abbildung 1a zeigt eine Reihe von Punkten, die durch eine Verteilung erzeugt wurden, die wir als positiv bezeichnen werden. Alle anderen möglichen Punkte, die nicht zur positiven Verteilung gehören, werden als negativ bezeichnet. Versuchen Sie mental eine Linie zu ziehen, die die positiven Punkte von allen möglichen negativen Punkten trennt. Diese Aufgabe wird übrigens als "Anomalieerkennung" bezeichnet.
Die Antwort ist hier

. 1.

. 1.
Sie haben sich vielleicht so etwas wie Abbildung 1b vorgestellt: Sie haben die Daten in einer Ellipse eingekreist. In der Tat funktionieren so viele Methoden zur Erkennung von Anomalien.
Lassen Sie uns nun das Problem ein wenig ändern: Geben Sie uns zusätzliche Informationen, dass eine gerade Linie positive von negativen Punkten trennen soll. Versuchen Sie es in Ihrem Kopf zu zeichnen.
Die Antwort ist hier
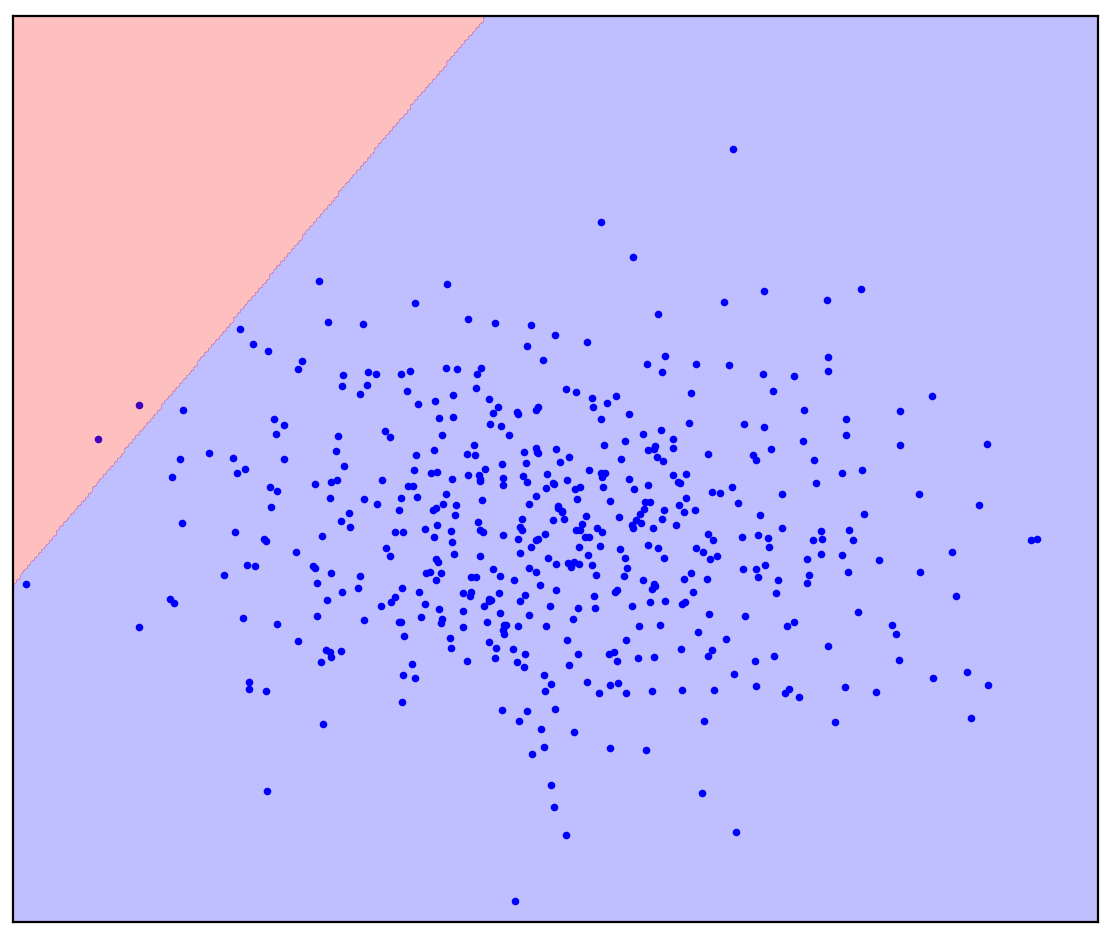
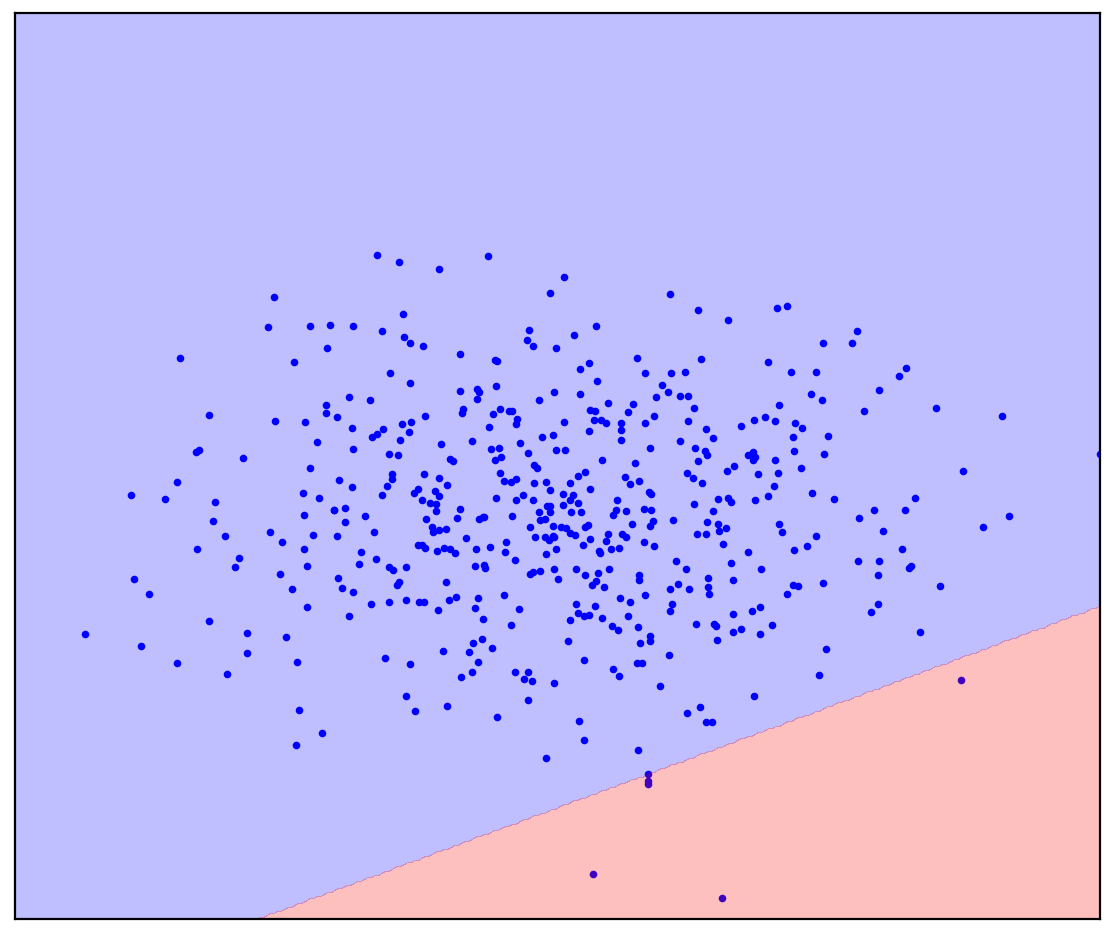
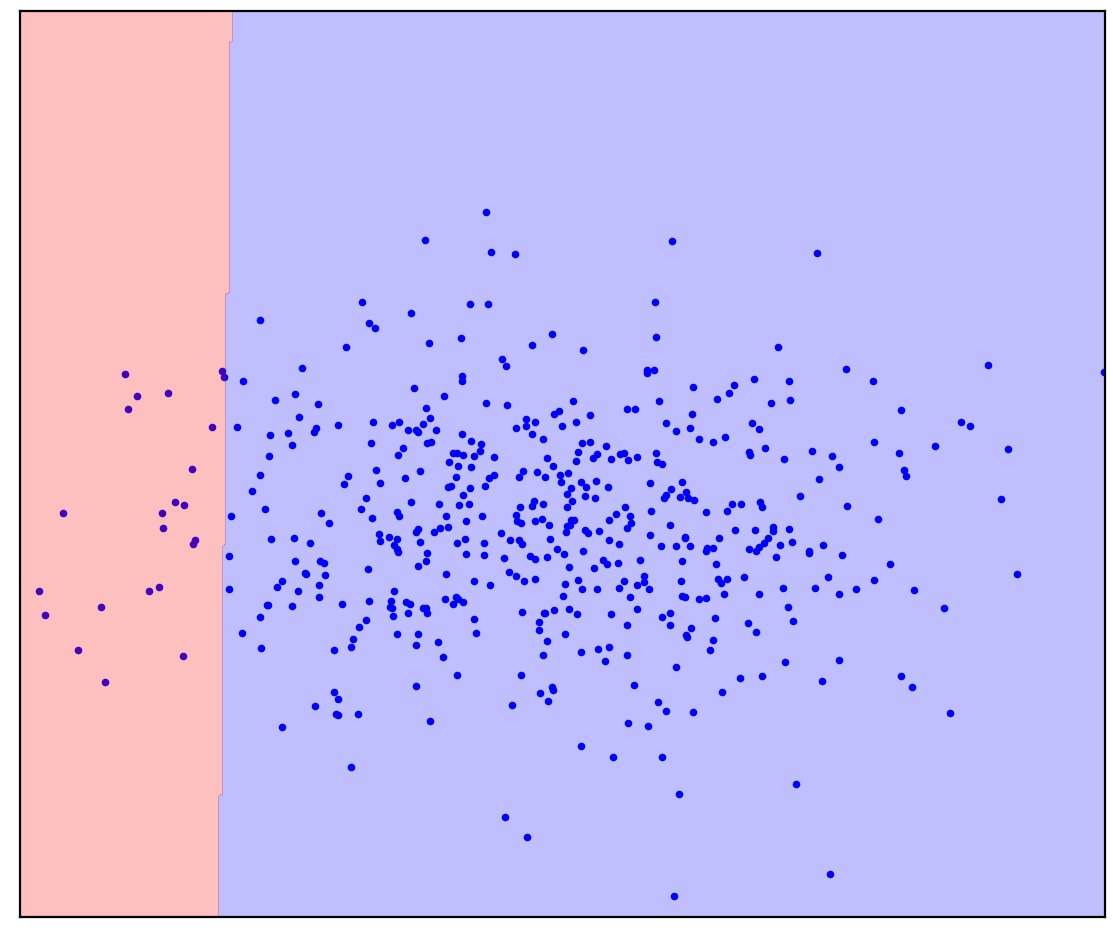
. 1. ( One-Class SVM)



. 1. ( One-Class SVM)
Bei einer geraden Trennlinie gibt es keine einzige Antwort. Es ist nicht klar, in welche Richtung eine gerade Linie gezogen werden soll.
Jetzt werde ich Abbildung 1d nicht zugewiesene Punkte hinzufügen, die eine Mischung aus positiv und negativ enthalten. Zum letzten Mal werde ich Sie bitten, sich geistig anzustrengen und sich eine Linie vorzustellen, die die positiven und negativen Punkte trennt. Diesmal können Sie jedoch unbeschriftete Daten verwenden!

Zahl: 1d. Positive (blau) und unbeschriftete (rot) Punkte. Nicht markierte Punkte setzen sich aus positiven und negativen Punkten zusammen
Die Antwort ist hier

. 1.

. 1.
Es wurde einfacher! Obwohl wir nicht im Voraus wissen, wie jeder einzelne nicht markierte Punkt erzeugt wird, können wir sie grob markieren, indem wir sie mit positiven vergleichen. Rote Punkte, die wie blau aussehen, sind wahrscheinlich positiv. Im Gegenteil, unterschiedliche sind wahrscheinlich negativ. Trotz der Tatsache, dass wir keine „reinen“ negativen Daten haben, können Informationen über diese aus der unbeschrifteten Mischung gewonnen und für eine genauere Klassifizierung verwendet werden. Dies ist, was die positiv-unbeschrifteten Lernalgorithmen tun, über die ich sprechen möchte.
Einführung
Positiv-unbeschriftetes (PU) Lernen kann übersetzt werden als "Lernen aus positiven und unbeschrifteten Daten". Tatsächlich ist PU-Lernen ein Analogon einer binären Klassifizierung für Fälle, in denen nur beschriftete Daten einer der Klassen vorhanden sind, aber eine unbeschriftete Mischung von Daten aus beiden Klassen verfügbar ist. Im allgemeinen Fall wissen wir nicht einmal, wie viele Daten in der Mischung einer positiven Klasse und wie viel einer negativen entsprechen. Basierend auf solchen Datensätzen möchten wir einen binären Klassifikator erstellen: der gleiche wie bei reinen Daten beider Klassen.
Betrachten Sie als Spielzeugbeispiel einen Klassifikator für Bilder von Katzen und Hunden. Wir haben einige Bilder von Katzen und viele weitere Bilder von Katzen und Hunden. Am Ausgang wollen wir einen Klassifikator erhalten: eine Funktion, die für jedes Bild die Wahrscheinlichkeit vorhersagt, mit der eine Katze dargestellt wird. Gleichzeitig kann der Klassifikator unsere vorhandene Bildmischung für Katzen und Hunde markieren. Gleichzeitig kann es schwierig / teuer / zeitaufwändig / unmöglich sein, Bilder für das Training des Klassifikators manuell zu markieren. Sie möchten dies ohne sie tun.
PU-Lernen ist eine ziemlich natürliche Aufgabe. In der realen Welt gefundene Daten sind oft schmutzig. Die Fähigkeit, aus schmutzigen Daten zu lernen, scheint ein nützlicher Life-Hack mit relativ hoher Qualität zu sein. Trotzdem habe ich paradoxerweise nur wenige Menschen getroffen, die von PU-Lernen gehört haben, und noch weniger, die über bestimmte Methoden Bescheid gewusst hätten. Also habe ich beschlossen, über diesen Bereich zu sprechen.

Zahl: 2. Jürgen Schmidhuber und Yann LeCun, NeurIPS 2020
Anwendung des PU-Lernens
Ich werde die Fälle, in denen PU-Lernen nützlich sein kann, informell in drei Kategorien einteilen.
Die erste Kategorie ist wahrscheinlich die offensichtlichste: PU-Lernen kann anstelle der üblichen binären Klassifizierung verwendet werden. Bei einigen Aufgaben sind die Daten von Natur aus leicht verschmutzt. Im Prinzip kann diese Verunreinigung ignoriert und ein herkömmlicher Klassifikator verwendet werden. Es ist jedoch möglich, die Verlustfunktion beim Training des Klassifikators (Kiryo et al., 2017) oder sogar die Vorhersagen selbst nach dem Training (Elkan & Noto, 2008) nur sehr wenig zu ändern , und die Klassifizierung wird genauer.
Betrachten Sie als Beispiel die Identifizierung neuer Gene, die für die Entwicklung von Krankheitsgenen verantwortlich sind. Der Standardansatz besteht darin, die bereits gefundenen Krankheitsgene als positiv und alle anderen Gene als negativ zu behandeln. Es ist klar, dass in diesen negativen Daten noch nicht gefundene Krankheitsgene vorhanden sein können. Darüber hinaus besteht die Aufgabe selbst darin, unter den "negativen" Daten nach solchen Krankheitsgenen zu suchen. Dieser interne Widerspruch wird hier bemerkt: (Yang et al., 2012) . Die Forscher wichen vom Standardansatz ab und betrachteten Gene, die nicht mit bereits entdeckten Krankheitsgenen zusammenhängen, als unmarkierte Mischung und wandten dann PU-Lernmethoden an.
Ein weiteres Beispiel ist das verstärkte Lernen aus Expertendemonstrationen. Die Herausforderung besteht darin, den Agenten so zu schulen, dass er sich wie ein Experte verhält. Dies kann mit der GAIL-Methode (Generative Adversarial Imitation Learning) erreicht werden. GAIL verwendet eine GAN-ähnliche Architektur (Generative Adversarial Networks): Der Agent generiert Trajektorien, sodass der Diskriminator (Klassifizierer) sie nicht von den Demonstrationen des Experten unterscheiden kann. Forscher von DeepMind haben kürzlich festgestellt, dass der Diskriminator in GAIL das PU-Lernproblem löst (Xu & Denil, 2019).... Normalerweise betrachtet der Diskriminator die Expertendaten als positiv und die erzeugten Daten als negativ. Diese Annäherung ist zu Beginn des Trainings genau genug, wenn der Generator keine Daten erzeugen kann, die positiv aussehen. Im Verlauf des Trainings sehen die generierten Daten jedoch eher wie Expertendaten aus, bis sie am Ende des Trainings für den Diskriminator nicht mehr unterscheidbar sind. Aus diesem Grund betrachten Forscher (Xu & Denil, 2019) die generierten Daten als unbeschriftete Daten mit einem variablen Mischungsverhältnis. Später wurde das GAN bei der Bilderzeugung auf ähnliche Weise modifiziert (Guo et al., 2020) .

Zahl: 3. PU-Lernen als Analogon zur Standard-PN-Klassifizierung
In der zweiten Kategorie kann das PU-Lernen zur Erkennung von Anomalien als Analogon zur Ein-Klassen-Klassifizierung (OCC) verwendet werden. Wir haben bereits in der Präambel gesehen, wie genau Daten ohne Tags helfen können. Alle OSS-Methoden sind ausnahmslos gezwungen, eine Annahme über die Verteilung negativer Daten zu treffen. Zum Beispiel ist es ratsam, positive Daten in eine Ellipse (eine Hypersphäre im mehrdimensionalen Fall) zu kreisen, außerhalb derer alle Punkte negativ sind. In diesem Fall gehen wir davon aus, dass die negativen Daten gleichmäßig verteilt sind (Blanchard et al., 2010)... Anstatt solche Annahmen zu treffen, können PU-Lernmethoden die Verteilung negativer Daten basierend auf unbeschrifteten Daten schätzen. Dies ist besonders wichtig, wenn sich die Verteilungen der beiden Klassen stark überschneiden (Scott & Blanchard, 2009) . Ein Beispiel für die Erkennung von Anomalien mithilfe von PU-Lernen ist die Erkennung gefälschter Überprüfungen (Ren et al., 2014) .

Zahl: 4. Ein Beispiel für eine gefälschte Bewertung
Aufdeckung von Korruption bei Auktionen für öffentliche Aufträge in Russland
Die dritte Kategorie des PU-Lernens kann auf Probleme zurückgeführt werden, bei denen weder eine binäre noch eine Einzelklassenklassifizierung verwendet werden kann. Als Beispiel erzähle ich Ihnen von unserem Projekt zur Aufdeckung von Korruption bei Auktionen russischer öffentlicher Aufträge (Ivanov & Nesterov, 2019) .
Laut Gesetz werden vollständige Daten zu allen Auktionen für öffentliche Aufträge für alle öffentlich zugänglich gemacht, die einen Monat damit verbringen möchten, sie zu analysieren. Wir haben Daten von mehr als einer Million Auktionen gesammelt, die von 2014 bis 2018 durchgeführt wurden. Wer hat wann und wie viel investiert, wer hat gewonnen, in welchem Zeitraum fand die Auktion statt, wer hat gehalten, was hat gekauft - all dies steht in den Daten. Aber natürlich gibt es kein Label "Korruption ist da", so dass Sie keinen gewöhnlichen Klassifikator erstellen können. Stattdessen haben wir PU-Lernen angewendet. Grundannahme: Teilnehmer mit einem unfairen Vorteil gewinnen immer. Unter dieser Annahme können die Verlierer in den Auktionen als fair (positiv) und die Gewinner als potenziell unehrlich (ohne Tags) angesehen werden.Wenn PU-Lernmethoden auf diese Weise eingerichtet werden, können sie verdächtige Muster in Daten finden, die auf subtilen Unterschieden zwischen Gewinnern und Verlierern beruhen. In der Praxis treten natürlich Schwierigkeiten auf: Ein genaues Design der Merkmale für den Klassifikator, eine Analyse der Interpretierbarkeit seiner Vorhersagen und eine statistische Überprüfung der Annahmen über Daten sind erforderlich.
Nach unserer sehr konservativen Schätzung sind etwa 9% der Auktionen in den Daten korrupt, wodurch der Staat etwa 120 Millionen Rubel pro Jahr verliert. Die Verluste scheinen nicht sehr groß zu sein, aber die von uns untersuchten Auktionen machen nur etwa 1% des Marktes für öffentliche Aufträge aus.


Zahl: 5. Der Anteil korrupter Auktionen für öffentliche Aufträge in verschiedenen Regionen Russlands (Ivanov & Nesterov, 2019)
Schlussbemerkungen
Um nicht den Eindruck zu erwecken, dass PU die Lösung für alle Probleme der Menschheit ist, werde ich die Fallstricke erwähnen. Bei einer herkömmlichen Klassifizierung kann der Klassifizierer umso genauer sein, je mehr Daten wir haben. Wenn wir die Datenmenge auf unendlich erhöhen, können wir uns außerdem dem idealen Klassifikator (gemäß der Bayes'schen Formel) nähern. Der Hauptfang des PU-Lernens ist also, dass es sich um ein schlecht gestelltes Problem handelt, dh um ein Problem, das selbst mit einer unendlichen Datenmenge nicht eindeutig gelöst werden kann. Die Situation wird besser, wenn der Anteil von zwei Klassen in unbeschrifteten Daten bekannt ist. Die Bestimmung dieses Anteils ist jedoch auch ein schlecht gestelltes Problem (Jain et al., 2016).... Das Beste, was wir definieren können, ist der Abstand, in dem sich das Verhältnis befindet. Darüber hinaus bieten PU-Lernmethoden häufig keine Möglichkeiten, diesen Anteil abzuschätzen und als bekannt zu betrachten. Es gibt separate Methoden, die dies schätzen (die Aufgabe wird als Gemischproportionsschätzung bezeichnet), aber sie sind häufig langsam und / oder instabil, insbesondere wenn die beiden Klassen in der Mischung sehr ungleichmäßig dargestellt sind.
In diesem Beitrag habe ich über die intuitive Definition und Anwendung des PU-Lernens gesprochen. Darüber hinaus kann ich über die formale Definition des PU-Lernens mit Formeln und deren Erklärungen sowie über klassische und moderne PU-Lernmethoden sprechen. Wenn dieser Beitrag Interesse weckt, schreibe ich eine Fortsetzung.
Referenzliste
Blanchard, G., Lee, G., & Scott, C. (2010). Semi-supervised novelty detection. Journal of Machine Learning Research, 11(Nov), 2973–3009.
Elkan, C., & Noto, K. (2008). Learning classifiers from only positive and unlabeled data. Proceeding of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining — KDD 08, 213. https://doi.org/10.1145/1401890.1401920
Guo, T., Xu, C., Huang, J., Wang, Y., Shi, B., Xu, C., & Tao, D. (2020). On Positive-Unlabeled Classification in GAN. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8385–8393.
Ivanov, D. I., & Nesterov, A. S. (2019). Identifying Bid Leakage In Procurement Auctions: Machine Learning Approach. ArXiv Preprint ArXiv:1903.00261.
Jain, S., White, M., Trosset, M. W., & Radivojac, P. (2016). Nonparametric semi-supervised learning of class proportions. ArXiv Preprint ArXiv:1601.01944.
Kiryo, R., Niu, G., du Plessis, M. C., & Sugiyama, M. (2017). Positive-unlabeled learning with non-negative risk estimator. Advances in Neural Information Processing Systems, 1675–1685.
Ren, Y., Ji, D., & Zhang, H. (2014). Positive Unlabeled Learning for Deceptive Reviews Detection. EMNLP, 488–498.
Scott, C., & Blanchard, G. (2009). Novelty detection: Unlabeled data definitely help. Artificial Intelligence and Statistics, 464–471.
Xu, D., & Denil, M. (2019). Positive-Unlabeled Reward Learning. ArXiv:1911.00459 [Cs, Stat]. http://arxiv.org/abs/1911.00459
Yang, P., Li, X.-L., Mei, J.-P., Kwoh, C.-K., & Ng, S.-K. (2012). Positive-unlabeled learning for disease gene identification. Bioinformatics, 28(20), 2640–2647.