Soziale Distanzmathematik ist eine Geometrie-Lektion

Die Herausforderung, Büros, Schulen und andere öffentliche Orte sicher wieder zu eröffnen und dabei die Menschen anderthalb Meter voneinander entfernt zu halten, besteht in einer Frage, die Mathematiker seit Jahrhunderten studieren.

Es mag den Anschein haben, dass ein Thema wie das Packen von Kugeln nur Mathematiker ansprechen wird. Wer sonst wäre daran interessiert, nach den effektivsten Möglichkeiten zu suchen, Kreise auf einer Ebene oder Kugeln im Raum zu platzieren?



Heute denken Millionen von Menschen auf der ganzen Welt über genau diese Aufgabe nach.



Die Bestimmung, wie Gebäude und öffentliche Räume sicher geöffnet werden können, während soziale Distanz eingehalten wird, ist insbesondere eine Übung in der Geometrie. Wenn jede Person mindestens anderthalb Meter von anderen Personen entfernt sein muss, müssen Sie nicht überlappende Kreise auf den Grundriss packen , um zu berechnen, wie viele Personen im Klassenzimmer oder im Esszimmer sitzen können .







Um das Coronavirus zu bekämpfen, müssen natürlich viel mehr Probleme gelöst werden als dieses geometrische. Dabei spielt jedoch die Packung von Kreisen und Kugeln eine Rolle - genau wie die Modellierung von Kristallstrukturen in der Chemie und abstrakten Nachrichtenräumen in der Informationstheorie. Diese scheinbar einfach zu beschreibende Aufgabe hat die größten Mathematiker der Geschichte beschäftigt, und die interessantesten Forschungen auf diesem Gebiet werden heute insbesondere in höheren Dimensionen durchgeführt. Zum Beispiel haben Mathematiker kürzlich den besten Weg gefunden, in 8- und 24-dimensionalen Räumen zu packen - eine Technik, die zur Optimierung von Fehlerkorrekturcodes benötigt wird, die sowohl in Mobiltelefonen als auch bei der Kommunikation mit Raumsonden verwendet werden. Schauen wir uns also einige der unerwarteten Komplikationen an, die auftreten, wenn wir versuchen, einen Raum mit dem einfachsten Formular zu füllen.



Unabhängig davon, ob Sie Orangen bei der Arbeit in Kartons verpacken oder Schüler mit sozialer Distanz sicher unterbringen, ist die Größe und Form Ihres Behälters für Ihre Aufgabe von entscheidender Bedeutung. Für die meisten Mathematiker geht es bei der Kugelpackungstheorie jedoch darum, den gesamten Raum zu füllen. In zwei Dimensionen bedeutet dies, die Ebene mit nicht zusammenhängenden Kreisen gleicher Größe abzudecken.



Hier ist ein Beispiel für das Packen von Kreisen in einer Ebene. Es sieht aus wie eine Draufsicht auf eine Limonade:







Sie können sich vorstellen, wie sich dieses Muster in alle Richtungen wiederholt, wie eine Fliese, die mit einer Ebene gepflastert wurde. Kleine Lücken zwischen den Kreisen weisen darauf hin, dass die Ebene nicht vollständig gefüllt ist. Bei Packkreisen ist dies jedoch zu erwarten. Uns interessiert, wie viel Prozent des Flugzeugs abgedeckt sind. Dies ist die "Packungsdichte" des jeweiligen Verfahrens.



Die obige Methode wird als quadratische Packung bezeichnet, und aus gutem Grund können die Mittelpunkte der Kreise als Eckpunkte der Quadrate dargestellt werden.







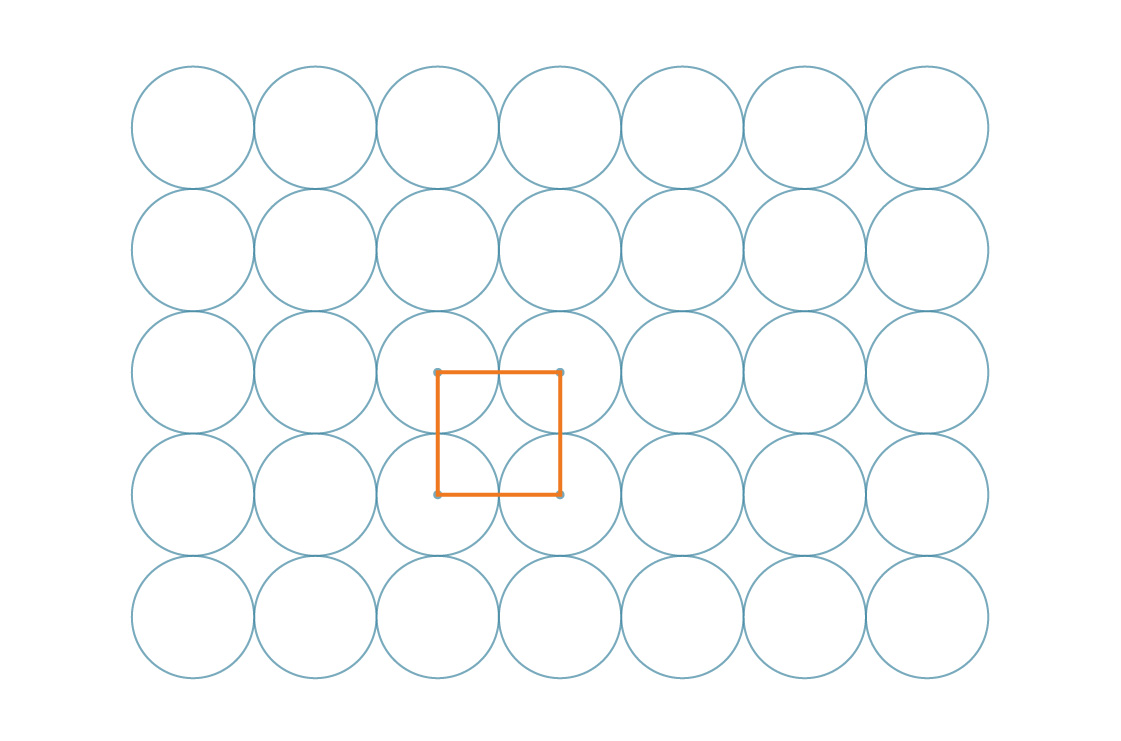
Tatsächlich kacheln diese Quadrate selbst die Ebene:







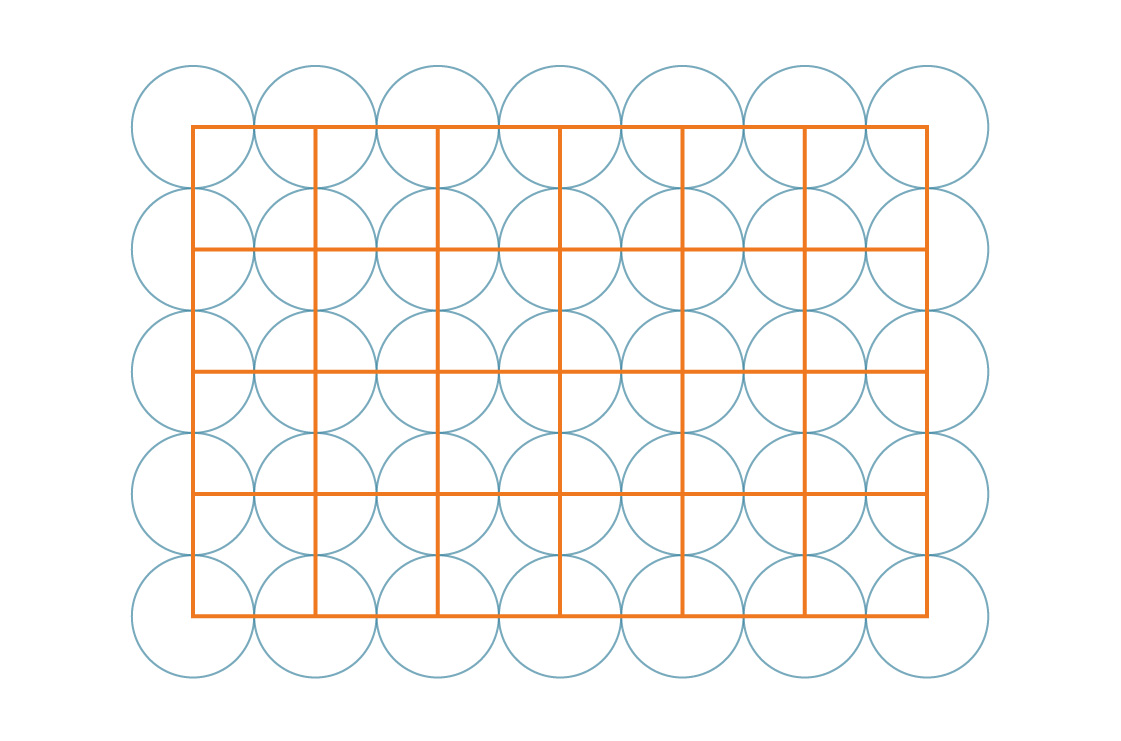
Unsere Aufgabe wird durch die Symmetrie des Musters erleichtert. Da diese Quadrate die gesamte Ebene periodisch abdecken, entspricht der Prozentsatz der von den Kreisen abgedeckten Ebene dem Prozentsatz des von den Kreisen abgedeckten Quadrats. Schauen wir uns eines dieser Quadrate an.







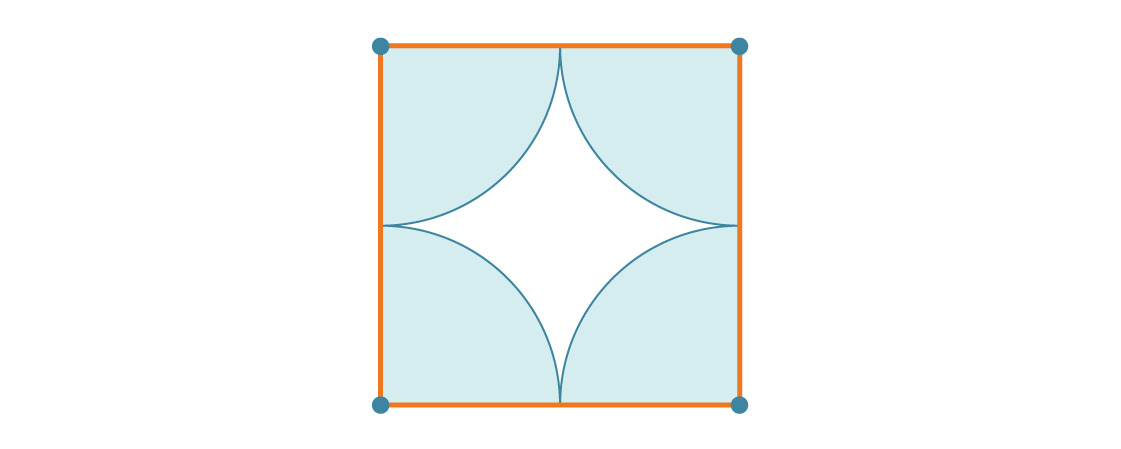
Angenommen, der Radius des Kreises ist r. Dies bedeutet, dass die Seitenlänge des Quadrats 2r beträgt. An jedem Eckpunkt des Quadrats befindet sich ein Viertel eines Kreises, sodass der Prozentsatz der Abdeckung jedes Quadrats einfach dem Verhältnis der Fläche eines vollen Kreises zur Fläche eines vollen Quadrats entspricht:

$$

$$\frac{\pi r^2}{(2r)^2} = \frac{\pi r^2}{4r^2} = \frac{\pi }{4} \approx 0,7854$$

Jedes Quadrat ist zu etwa 78,54% mit Kreisen bedeckt. Angesichts der Kacheln der Ebene ist das gesamte Quadrat zu etwa 78,54% mit Kreisen bedeckt. Dies ist die Dichte der quadratischen Packung. Beachten Sie, dass der Radius r aus der Antwort verschwunden ist. Und das macht Sinn: Egal wie groß die Kreise sind, es gibt immer noch vier Viertel eines Kreises in einem Quadrat.



Wenn Sie versucht haben, Getränkedosen auf der Seite so zu falten, und sie sich verschoben und ausgefüllt haben, wissen Sie, dass es eine andere Möglichkeit gibt, die Kreise in eine Ebene zu packen:







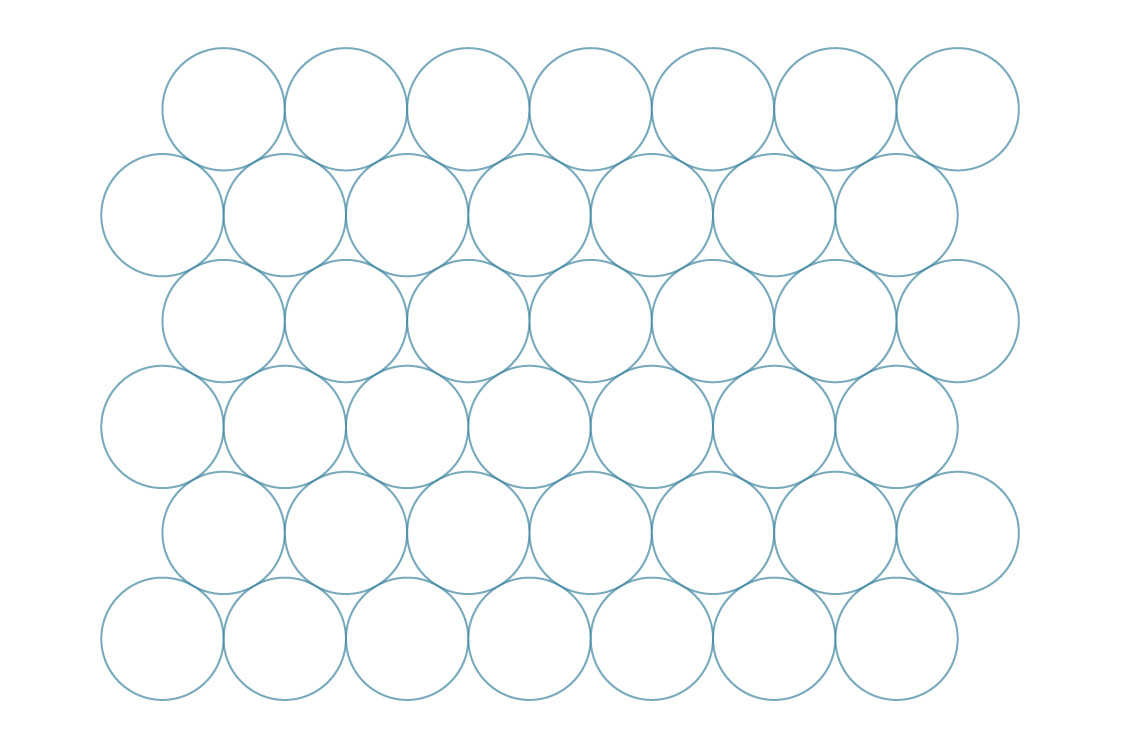
Gehen wir ähnlich vor wie in der vorherigen und stellen Sie sich vor, dass die Kreismittelpunkte in diesem Fall regelmäßige Sechsecke bilden ...







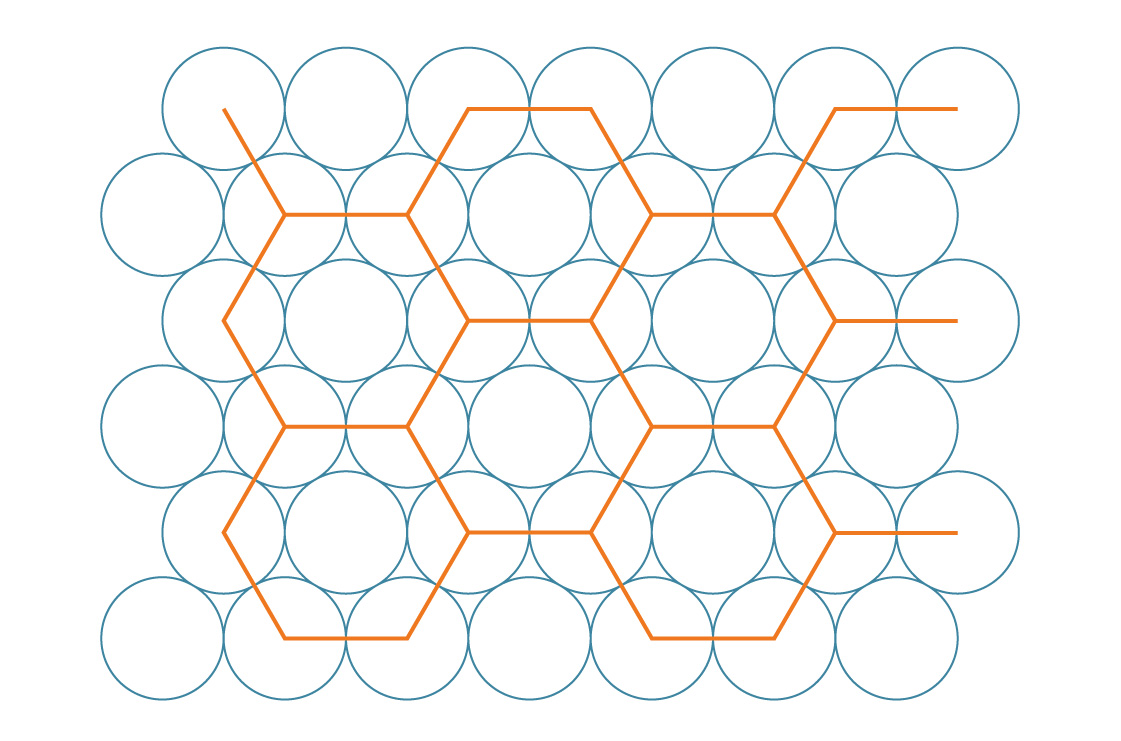
Wir nennen diese sechseckige Packung. Es scheint, dass diese Methode Lücken effizienter als quadratisch füllt. Um dies zu überprüfen, vergleichen wir ihre Packungsdichten. Sechsecke kacheln wie Quadrate die Ebene vollständig, sodass wir die Dichte dieser Methode durch Analyse eines einzelnen Sechsecks bestimmen können.







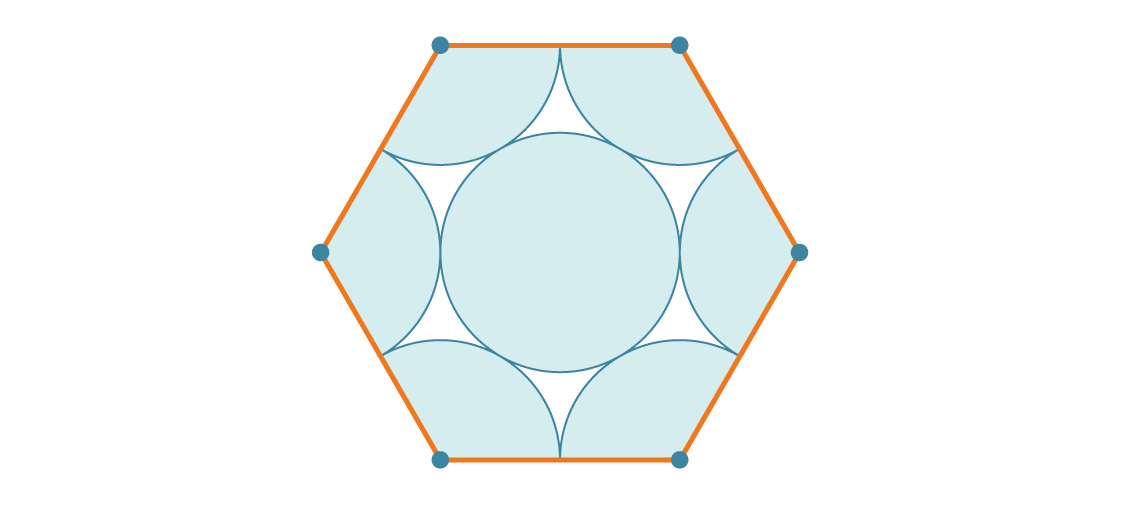
Welcher Teil des Sechsecks ist mit Kreisen bedeckt? Da ein reguläres Sechseck einen Innenwinkel von 120 ° hat, befindet sich in jeder Ecke ein Drittel eines Kreises. Es stellt sich heraus, dass zwei Kreise voll sind und der mittlere Kreis an dritter Stelle steht. Daher ist jedes Sechseck von drei Kreisen bedeckt. Wenn der Radius jedes Kreises r ist, beträgt die Fläche 3πr².







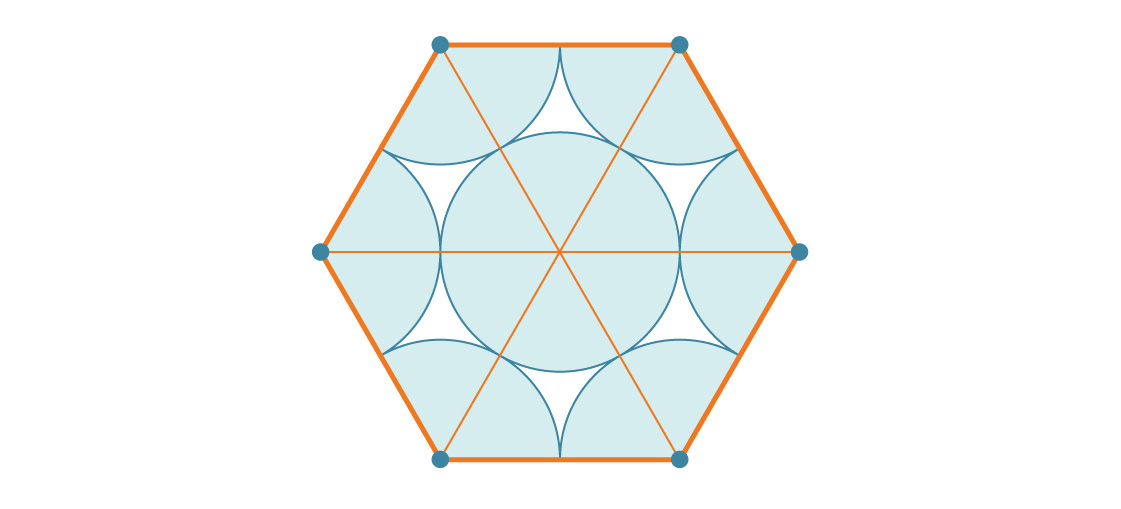
Wie ist das mit der Fläche eines Sechsecks zu vergleichen? Ein Sechseck mit der Seitenlänge s besteht aus sechs gleichseitigen Dreiecken mit der Seitenlänge s, von denen jedes s ² √3 / 4 ist. Daher beträgt die Fläche des Sechsecks 6 * s ² √3 / 4 = 6 s ² √3 / 4. Da die Seitenlänge unseres Sechsecks 2r beträgt, beträgt seine Fläche:

$$

$$\frac{6 s^2 \sqrt3}{4} = \frac{6 (2r)^2 \sqrt3}{4} = \frac{24 r^2 \sqrt3}{4} = 6 r^2 \sqrt3$$

Jetzt können Sie den Prozentsatz des von den Kreisen bedeckten Sechsecks berechnen (indem Sie die Fläche der sechs Kreise durch die Fläche des Sechsecks teilen):

$$

$$\frac{3 \pi r^2}{6 r^2 \sqrt3} = \frac{3 \pi}{6 \sqrt3} = \frac{\pi}{2 \sqrt3} \approx 0,9069$$

Jedes Sechseck ist zu etwa 90,69% mit Kreisen bedeckt, sodass diese Verpackung viel effizienter ist als eine quadratische. Beachten Sie, wie der Radius des Kreises wie erwartet wieder verschwindet. Tatsächlich gibt es keine effizientere Verpackung.



Aber es war nicht leicht, es zu beweisen. Berühmte Mathematiker wie Joseph Louis Lagrange und Karl Friedrich Gauss begannen im späten 18. und frühen 19. Jahrhundert damit, aber das Problem wurde erst in den 1940er Jahren vollständig gelöst, indem alle möglichen Anordnungen - periodisch und nicht periodisch - sorgfältig bearbeitet wurden. Die Tatsache, dass es so lange gedauert hat, das Problem in zwei Dimensionen zu lösen, in denen alles leicht vorstellbar ist, kann als Warnung für das dienen, was uns in höheren Dimensionen erwartet.



Das dreidimensionale Packen von Kugeln ist eine viel schwierigere Aufgabe, obwohl es einige Ähnlichkeiten mit seinem zweidimensionalen Cousin aufweist. Zum Beispiel bestehen die zweidimensionalen Packungen, die wir betrachtet haben, aus einer Schicht.







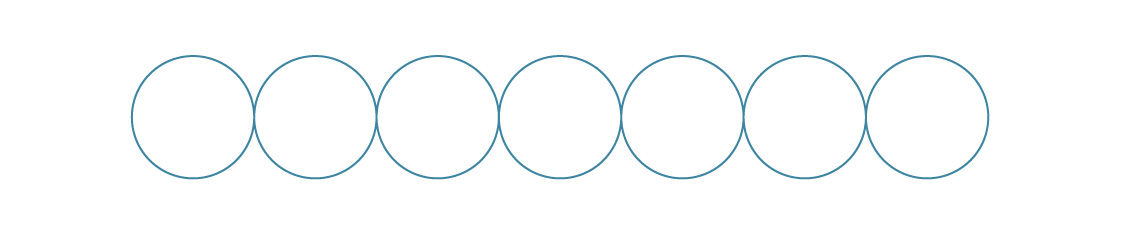
Für ein quadratisches Paket legen wir jede Schicht auf die vorherige.







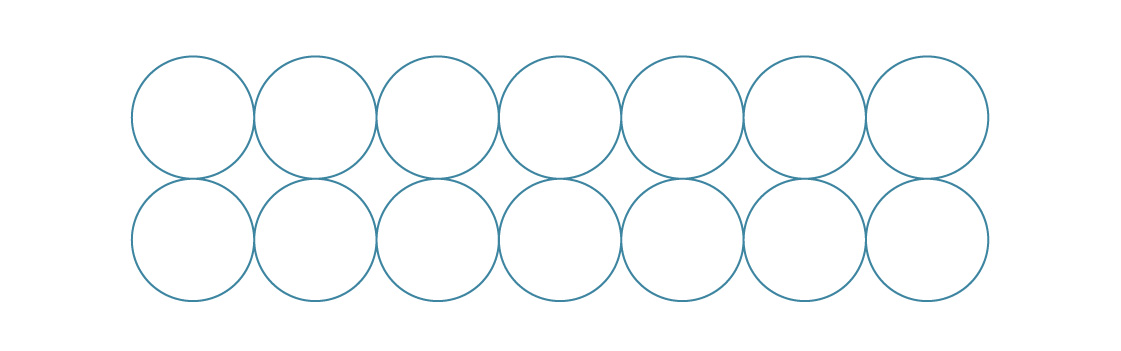
Für die sechseckige Packung haben wir neue Schichten zwischen die vorherigen gelegt.







Je nachdem, wie wir Kopien verschiedener Schichten kombinieren, werden unterschiedliche Verpackungen erhalten.



In drei Dimensionen erzeugt diese Anordnung von Schichten übereinander grundlegend unterschiedliche Packungen.







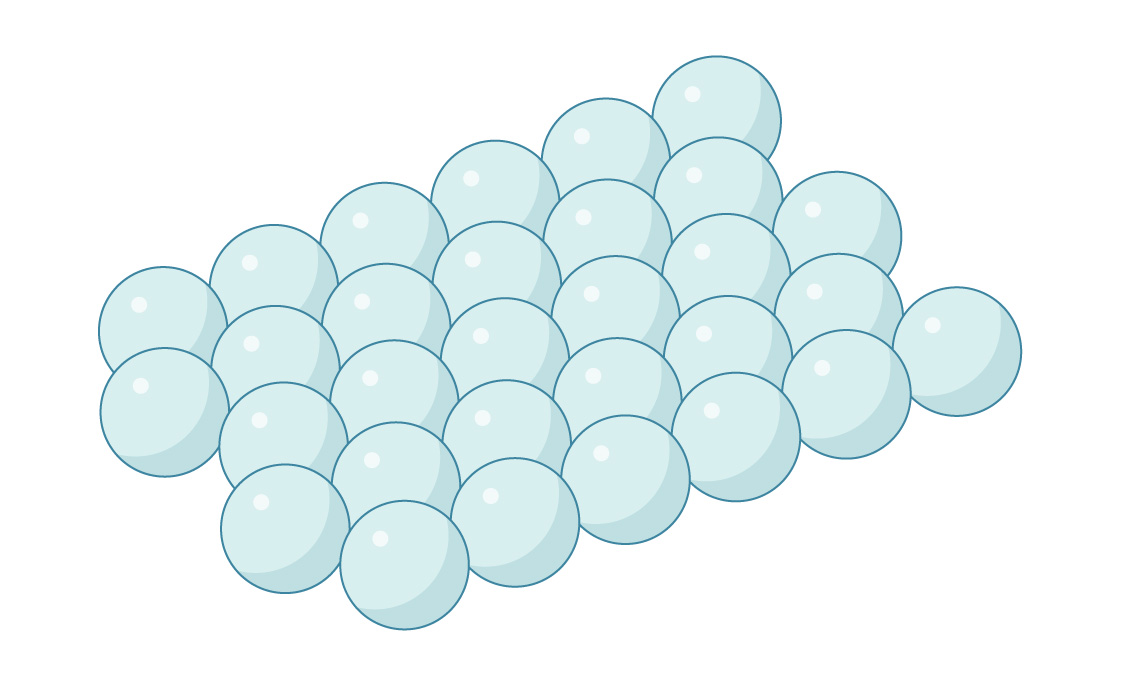
Dies ist eine Schicht von Kugeln, die hexagonal gepackt sind, wie unsere optimale Packung von Kreisen in einer Ebene nahe legt. Ebenso können Sie die zweite Ebene über die erste legen, indem Sie Kugeln in den Zwischenräumen zwischen den unteren Kugeln platzieren.







In drei Dimensionen wird die Geometrie jedoch etwas komplizierter. In jeder Kugelschicht ist der Abstand zwischen benachbarten Lücken geringer als der Abstand zwischen den Zentren der Kugeln. Daher können Sie nicht in jede Lücke eine Kugel stecken - sie würden sich schneiden. Daher werden die Lücken in den beiden Ebenen ausgerichtet, um Kanäle zu erstellen, die durch das Paket verlaufen.







Es gibt zwei Möglichkeiten, die dritte Ebene zu platzieren. Sie können die Lücken an den unteren ausrichten und die Kanäle offen lassen. Hier ist eine Seitenansicht dieser Anordnung:







Um die Kanäle offen zu halten, müssen Sie die Kugeln in der dritten Schicht direkt über den Kugeln der ersten Schicht platzieren. Diese Anordnung von Kugeln wird als "hexagonal dichte Packung" (Silo) bezeichnet. Wenn Sie sie von oben betrachten, können Sie die offenen Lücken sehen, die durch sie hindurchgehen.







Eine weitere Option zum Platzieren der dritten Ebene ist das Schließen der Kanäle. Die Kugeln in der dritten Schicht befinden sich direkt über den Lücken der ersten:







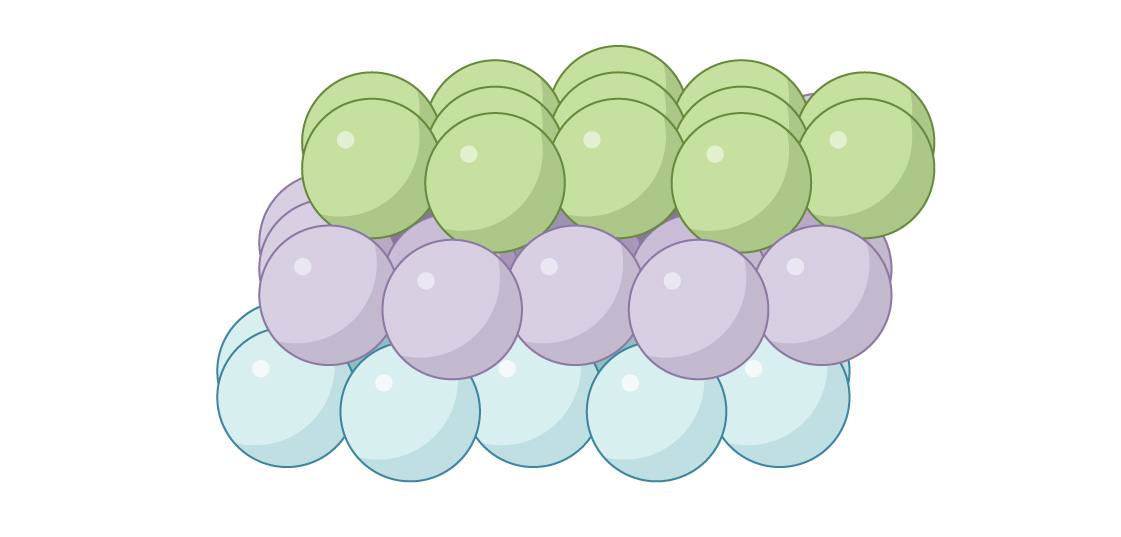
Dies wird als "flächenzentrierte kubische" (FCC) oder "kubisch enge Packung" bezeichnet. Von oben gesehen gibt es keine Lücken.







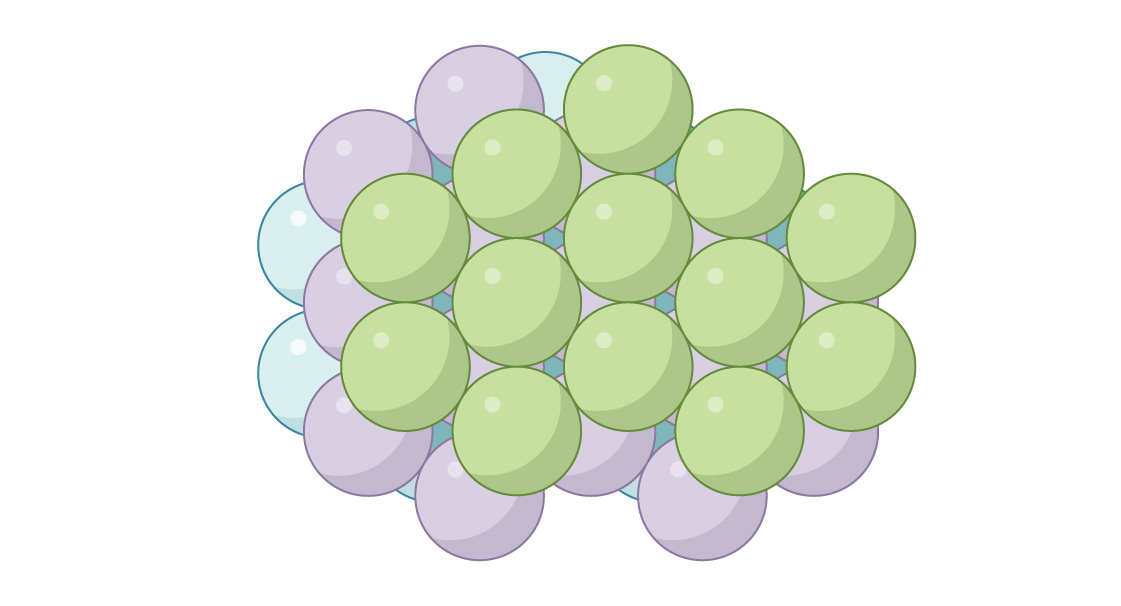
Diese beiden ähnlichen, aber grundlegend unterschiedlichen Anordnungen entstehen in der Chemie und beschreiben die Anordnung von Atomen in verschiedenen Materialien. Beispielsweise hat die Struktur in Metallen wie Silber und Gold die Form von HA und in Metallen wie Zink und Titansilos. Mit jeder der beiden Methoden können Sie den Raum mit Kugeln füllen. Bei der Silomethode befinden sich die Kugeln in jeder zweiten Schicht genau gleich und in der GK - in jeder dritten. Sie können unendlich viele verschiedene Verpackungen erstellen, indem Sie beide Methoden kombinieren. Es ist jedoch interessant, dass sowohl Silo als auch GK eine optimale Verpackung bieten! Ihre Packungsdichte ist nicht nur gleich, π 3√2 ≈ 0,7405 ist die dichteste Packung im dreidimensionalen Raum. Der berühmte Mathematiker und Astronom Johannes Kepler schlug dies 1611 vor, aber ein vollständiger BeweisNur der Mathematiker Thomas Hales konnte 1998 darauf schließen.







Es gibt mehr Platz im 3D-Raum und wir haben mehr Möglichkeiten, die Kugeln effektiv zu packen. Wenn Sie Abmessungen hinzufügen, nimmt die Komplexität der Verpackung nur zu - es gibt mehr Platz, mehr Optionen und es ist schwerer vorstellbar. Außerdem werden die Kugeln in höheren Dimensionen kleiner!







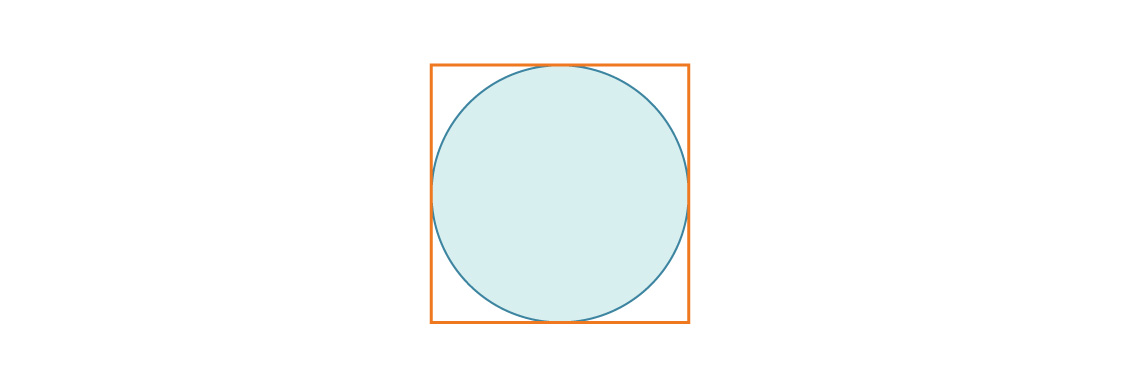
Stellen Sie sich einen Kreis vor, der in ein Quadrat mit der Seitenlänge 1 eingeschrieben ist.



Der Radius des Kreises beträgt r = 1/2. Das Verhältnis der Fläche des Kreises zur Fläche des Quadrats beträgt also:

$$

$$\frac{\pi r^2}{s^2} = \frac{\pi (\frac{1}{2})^2}{1^2} = \frac{\pi }{4} \approx 0,7854$$

Das entspricht auch der Packungsdichte des Quadrats in zwei Dimensionen.



Betrachten wir nun das Volumen einer Kugel, die in einen Einheitswürfel eingeschrieben ist.







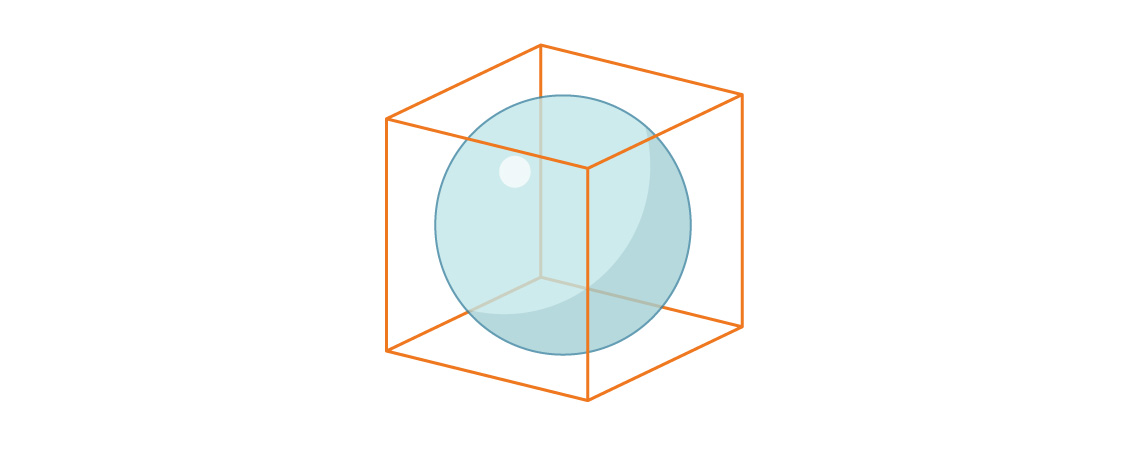
Der Radius der Kugel ist wieder gleich r = 1/2, daher ist das Verhältnis des Volumens der Kugel zum Volumen des Würfels:

$$

$$\frac{\frac{4}{3}\pi r^3}{s^3} = \frac{\frac{4}{3}\pi (\frac{1}{2})^3}{1^3} = \frac{4}{3}\pi (\frac{1}{8}) = \frac{\pi}{6} \approx 0,5236$$

Beachten Sie, dass der Anteil des Würfels, den die beschriftete Kugel in drei Dimensionen einnimmt, geringer ist als der Anteil des Quadrats, das der eingeschriebene Kreis in zwei Dimensionen einnimmt. Dieses Muster setzt sich fort: Mit zunehmenden Abmessungen nimmt dieses Verhältnis ab. Wenn n wächst, nehmen n-dimensionale Kugeln immer weniger n-dimensionalen Raum ein.



Dies kann mit Algebra gezeigt werden, aber es kann auch verstanden werden, wenn Sie über Winkel nachdenken. In jeder Dimension kann eine n-dimensionale Kugel in einen n-dimensionalen Würfel eingeschrieben werden. Die Kugel berührt die Ränder des Würfels, erreicht jedoch nicht die Ecken. Daher gibt es um jede Ecke einen Bereich, der sich innerhalb des Würfels, aber außerhalb der Kugel befindet. Eine n-dimensionale Box hat jedoch 2 ⁿWinkel, dh mit einer Zunahme von n wächst die Anzahl der Bereiche, die nicht von der Kugel bedeckt sind, exponentiell. Außerdem vergrößert sich auch der Abstand zwischen den Ecken und der Kugel. Dies bedeutet, dass auf lange Sicht der Raum innerhalb des n-dimensionalen Würfels, aber außerhalb der n-dimensionalen Kugel, den von der Kugel eingenommenen Raum einfach zerquetscht.



Wenn Ihnen die Kontraktion der Kugeln seltsam genug erscheint, haben die an der Packung der Kugeln beteiligten Mathematiker in den Dimensionen 8 und 24 etwas noch Unerwartetes bemerkt. In diesen Dimensionen schrumpfen die Kugeln gerade so weit, dass sie die Lücken zwischen den neuen Kugeln füllen können, was zu einer ultradichten Packung in diesen Dimensionen führt. ... Es wurde eine Hypothese über die Optimalität dieser speziellen Methoden aufgestellt, die jedoch erst 2016 bekannt wurde, als Marina Vyazovskaya diesen Satz bewiesfür 8-dimensionalen Raum. Eine Woche später erweiterten Vyazovskaya und ihre Assistenten ihre Methode, um den Fall im 24-dimensionalen Raum zu beweisen.



Aus Vyazovskayas Arbeit folgt, dass wir jetzt die effektivsten Methoden zum Packen von Kugeln in den Dimensionen 1, 2, 3, 8 und 24 kennen. In anderen Dimensionen gibt es jedoch noch viel zu tun. Holen Sie also die Orangen und Getränkedosen heraus und beginnen Sie zu experimentieren. Sie können derjenige sein, der die wichtigen Lücken füllen kann.

Übungen

1. Nehmen wir an, wir haben mit dem Packen der Koordinatenebene begonnen, wie in den folgenden Bildern gezeigt. Der Mittelpunkt des unteren linken Kreises befindet sich am Punkt (0, 0) und der Mittelpunkt des unteren rechten Kreises befindet sich am Punkt (2, 0).







Wo ist der Mittelpunkt des dritten Kreises?



2. Unten ist der Beginn der "einfachen kubischen" Packung von Kugeln. Was ist die Packungsdichte eines solchen Schemas?







3. Hier beginnt das Packen des Flugzeugs in reguläre Achtecke.







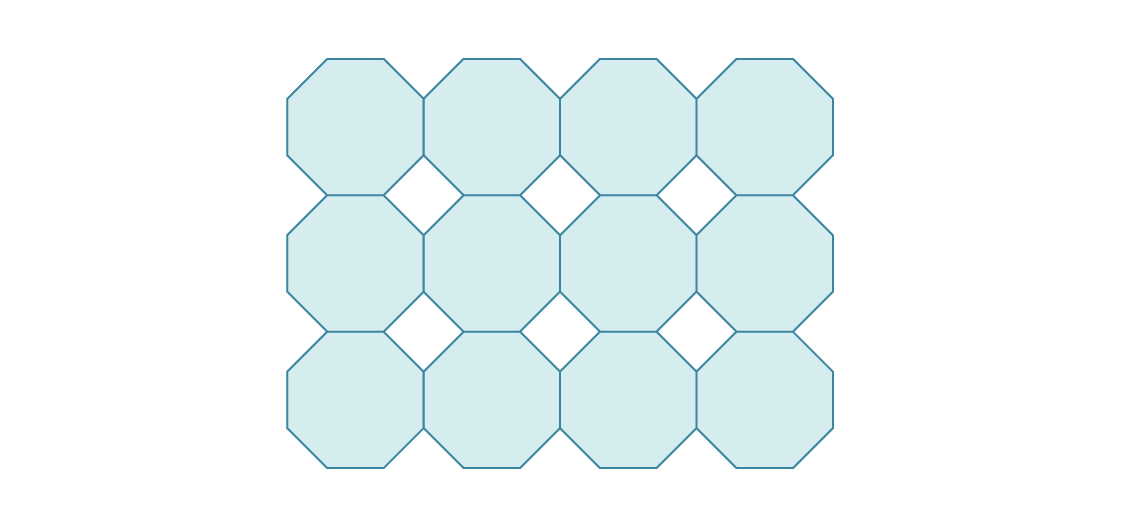
Was ist die Dichte eines solchen Pakets?

Antworten

Siehe auch:

• " Google veröffentlicht Sodar, ein AR-Tool zur Anzeige sozialer Distanz "
• " Meta-Studie zeigt die Wirksamkeit von Masken und Distanzierung gegen SARS-CoV-2 (COVID-19) "
• " COVID-19: Epidemic Parametric Prediction Model "