In diesem Artikel lernen Sie
- Was ist CNN und wie funktioniert es?
- Was ist eine Feature-Map?
- Was ist maximales Pooling?
- Verlustfunktionen für verschiedene Deep-Learning-Aufgaben
Kleine Einführung
Diese Artikelserie soll ein intuitives Verständnis dafür vermitteln, wie Deep Learning funktioniert, welche Aufgaben es gibt, welche Netzwerkarchitekturen es gibt und warum eines besser ist als das andere. Es wird nur wenige spezifische Dinge im Sinne von "wie man es umsetzt" geben. Wenn Sie auf jedes Detail eingehen, ist das Material für die meisten Zuschauer zu komplex. Es wurde bereits geschrieben, wie der Berechnungsgraph funktioniert oder wie die Rückausbreitung durch Faltungsschichten funktioniert. Und vor allem ist es viel besser geschrieben, als ich erklären würde.
Im vorherigen Artikel haben wir FCNN besprochen - was es ist und was die Probleme sind. Die Lösung für diese Probleme liegt in der Architektur von Faltungs-Neuronalen Netzen.
Faltungsneurale Netze (CNN)
Faltungs-Neuronales Netzwerk. Es sieht so aus (vgg-16-Architektur):
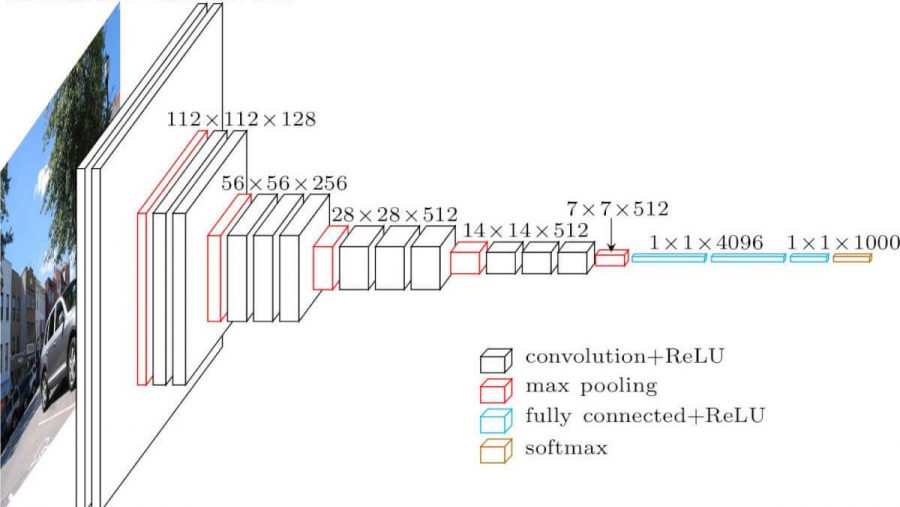
Was sind die Unterschiede zu einem vollständig vermaschten Netzwerk? Die verborgenen Schichten haben jetzt eine Faltungsoperation.
So sieht die Faltung aus:

Wir nehmen einfach ein Bild (vorerst - einkanalig), nehmen einen Faltungskern (Matrix), der aus unseren Trainingsparametern besteht, "überlagern" den Kern (normalerweise 3x3) mit dem Bild und führen eine elementweise Multiplikation aller Pixelwerte des Bildes durch, das den Kernel trifft. Dann wird alles zusammengefasst (Sie müssen auch den Bias-Parameter - Offset hinzufügen), und wir erhalten eine Zahl. Diese Nummer ist das Element der Ausgabeebene. Wir bewegen diesen Kern mit einem Schritt über unser Bild und erhalten die nächsten Elemente. Aus solchen Elementen wird eine neue Matrix aufgebaut, auf die der nächste Faltungskern angewendet wird (nachdem die Aktivierungsfunktion darauf angewendet wurde). Wenn das Eingabebild dreikanalig ist, ist der Faltungskern ebenfalls dreikanalig - ein Filter.
Aber hier ist nicht alles so einfach. Diese Matrizen, die wir nach der Faltung erhalten, werden Feature-Maps genannt, da sie einige Features der vorherigen Matrizen speichern, jedoch in einer anderen Form. In der Praxis werden mehrere Faltungsfilter gleichzeitig verwendet. Dies geschieht, um so viele Merkmale wie möglich auf die nächste Faltungsschicht zu "bringen". Mit jeder Schicht der Faltung werden unsere Merkmale, die sich im Eingabebild befanden, immer mehr in abstrakten Formen dargestellt.
Noch ein paar Anmerkungen:
- Nach dem Falten wird unsere Feature-Map kleiner (in Breite und Höhe). Manchmal wird die Null-Füllmethode verwendet, um die Breite und Höhe schwächer oder gar nicht zu verringern (gleiche Faltung) - mit Nullen "entlang der Kontur" der Eingabe-Feature-Map.
- Nach der letzten Faltungsschicht verwenden Klassifizierungs- und Regressionsaufgaben mehrere vollständig verbundene Schichten.
Warum ist es besser als FCNN
- Wir können jetzt weniger trainierbare Parameter zwischen den Ebenen haben
- Wenn wir nun Merkmale aus dem Bild extrahieren, berücksichtigen wir nicht nur ein einzelnes Pixel, sondern auch Pixel in der Nähe (Identifizierung bestimmter Muster im Bild).
Max Pooling
Es sieht so aus:
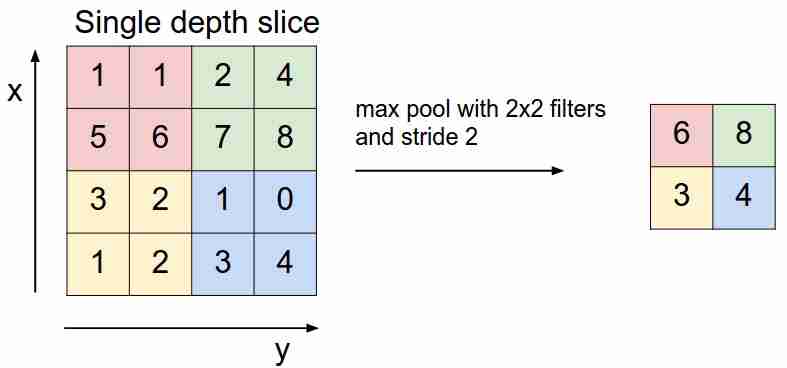
Wir "gleiten" mit einem Filter über unsere Feature-Map und wählen nur die wichtigsten Features (in Bezug auf das eingehende Signal als Wert) aus, wodurch die Dimension der Feature-Map verringert wird. Es gibt auch ein durchschnittliches (gewichtetes) Pooling, wenn wir die Werte mitteln, die in den Filter fallen, aber in der Praxis ist das maximale Pooling besser anwendbar.
- Diese Schicht hat keine trainierbaren Parameter
Verlustfunktionen
Wir speisen das Netzwerk X dem Eingang zu, erreichen den Ausgang, berechnen den Wert der Verlustfunktion, führen den Backpropagation-Algorithmus durch - so lernen moderne neuronale Netze (bisher sprechen wir nur über überwachtes Lernen).
Abhängig von den Aufgaben, die neuronale Netze lösen, werden verschiedene Verlustfunktionen verwendet:
- Regressionsproblem . Meistens verwenden sie die Funktion des mittleren quadratischen Fehlers (MSE).
- Klassifizierungsproblem . Sie verwenden hauptsächlich Kreuzentropieverlust.
Wir erwägen noch keine anderen Aufgaben - dies wird in den folgenden Artikeln erörtert. Warum genau solche Funktionen für solche Aufgaben? Hier müssen Sie die Maximum-Likelihood-Schätzung und die Mathematik eingeben. Wen kümmert es - ich habe hier darüber geschrieben .
Fazit
Ich möchte Ihre Aufmerksamkeit auch auf zwei Dinge lenken, die in neuronalen Netzwerkarchitekturen verwendet werden, einschließlich Faltungsarchitekturen - Dropout (Sie können es hier lesen ) und Batch-Normalisierung . Ich kann das Lesen nur empfehlen.
Im nächsten Artikel werden wir die CNN-Architektur analysieren und verstehen, warum eine besser ist als die andere.