Dabei ist q die Ladung des Partikels, r ij der Abstand zwischen den Partikeln, C ist abhängig von der Wahl der Maßeinheiten eine Konstante. In SI ist es -In SGS - 1 ist C in meinem Programm (wobei Energie in Elektronenvolt, Abstand in Angström und Ladung in Elementarladungen ausgedrückt wird) ungefähr gleich 14.3996.
Also was, sagst du? Fügen Sie einfach den entsprechenden Begriff zum Paarpotential hinzu und Sie sind fertig. Am häufigsten werden jedoch bei der MD-Modellierung periodische Randbedingungen verwendet, d.h. Das simulierte System ist von allen Seiten von einer unendlichen Anzahl seiner virtuellen Kopien umgeben. In diesem Fall interagiert jedes virtuelle Bild unseres Systems mit allen geladenen Teilchen im System gemäß dem Coulombschen Gesetz. Und da die Coulomb-Wechselwirkung mit der Entfernung sehr schwach abnimmt (wie 1 / r), ist es nicht so einfach, sie zu verwerfen, da wir sie nicht aus dieser und jener Entfernung berechnen können. Eine Reihe der Form 1 / x divergiert, d.h. seine Menge kann im Prinzip unbegrenzt wachsen. Und jetzt salzen Sie nicht eine Schüssel Suppe? Wird es dich mit Elektrizität töten?
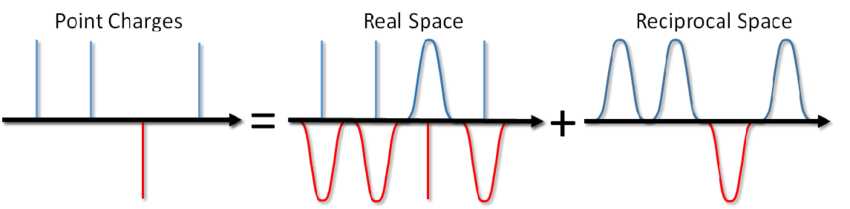
... Sie können nicht nur die Suppe salzen, sondern auch die Energie der Coulomb-Wechselwirkung unter periodischen Randbedingungen berechnen. Diese Methode wurde bereits 1921 von Ewald zur Berechnung der Energie eines Ionenkristalls vorgeschlagen (siehe auch Wikipedia ). Das Wesentliche der Methode besteht darin, Punktladungen zu screenen und dann die Screening-Funktion zu subtrahieren. In diesem Fall wird ein Teil der elektrostatischen Wechselwirkung auf einen kurz wirkenden reduziert und kann einfach auf übliche Weise abgeschnitten werden. Der verbleibende Fernbereichsteil wird effektiv im Fourierraum summiert. Ohne die Schlussfolgerung, die in Blinovs Artikel oder in demselben Buch von Frenkel und Smith zu sehen ist , werde ich sofort eine Lösung namens Ewald-Summe aufschreiben:
wobei α ein Parameter ist, der das Verhältnis von Berechnungen in Vorwärts- und Rückwärtsräumen reguliert, k Vektoren im Reziprokraum sind, über den die Summierung stattfindet, V das Volumen des Systems (im Vorwärtsraum) ist. Der erste Teil (E real ) ist kurzreichweitig und wird im selben Zyklus wie die anderen Paarpotentiale berechnet, siehe die Funktion real_ewald im vorherigen Artikel. Der letzte Beitrag (E onst ) ist eine Korrektur der Selbstinteraktion und wird oft als "konstanter Teil" bezeichnet, da er nicht von den Koordinaten der Partikel abhängt. Die Berechnung ist trivial, daher konzentrieren wir uns nur auf den zweiten Teil der Ewald-Summe (E rec), Summation im Reziprokraum. Natürlich gab es zum Zeitpunkt der Ableitung von Ewald keine molekulare Dynamik, ich konnte nicht finden, wer diese Methode zuerst bei MD verwendete. Heutzutage enthält jedes Buch über MD seine Präsentation als eine Art Goldstandard. Um zu buchen, lieferte Allen sogar Beispielcode in Fortran. Glücklicherweise habe ich immer noch den Code, der einmal in C für die sequentielle Version geschrieben wurde. Er muss nur noch parallelisiert werden (ich habe mir erlaubt, einige Variablendeklarationen und andere unbedeutende Details wegzulassen):
void ewald_rec()
{
int mmin = 0;
int nmin = 1;
// iexp(x[i] * kx[l]),
double** elc;
double** els;
//... iexp(y[i] * ky[m])
double** emc;
double** ems;
//... iexp(z[i] * kz[n]),
double** enc;
double** ens;
// iexp(x*kx)*iexp(y*ky)
double* lmc;
double* lms;
// q[i] * iexp(x*kx)*iexp(y*ky)*iexp(z*kz)
double* ckc;
double* cks;
//
eng = 0.0;
for (i = 0; i < Nat; i++) //
{
// emc/s[i][0] enc/s[i][0]
// elc/s , .
elc[i][0] = 1.0;
els[i][0] = 0.0;
// iexp(kr)
sincos(twopi * xs[i] * ra, els[i][1], elc[i][1]);
sincos(twopi * ys[i] * rb, ems[i][1], emc[i][1]);
sincos(twopi * zs[i] * rc, ens[i][1], enc[i][1]);
}
// emc/s[i][l] = iexp(y[i]*ky[l]) ,
for (l = 2; l < ky; l++)
for (i = 0; i < Nat; i++)
{
emc[i][l] = emc[i][l - 1] * emc[i][1] - ems[i][l - 1] * ems[i][1];
ems[i][l] = ems[i][l - 1] * emc[i][1] + emc[i][l - 1] * ems[i][1];
}
// enc/s[i][l] = iexp(z[i]*kz[l]) ,
for (l = 2; l < kz; l++)
for (i = 0; i < Nat; i++)
{
enc[i][l] = enc[i][l - 1] * enc[i][1] - ens[i][l - 1] * ens[i][1];
ens[i][l] = ens[i][l - 1] * enc[i][1] + enc[i][l - 1] * ens[i][1];
}
// K-:
for (l = 0; l < kx; l++)
{
rkx = l * twopi * ra;
// exp(ikx[l]) ikx[0]
if (l == 1)
for (i = 0; i < Nat; i++)
{
elc[i][0] = elc[i][1];
els[i][0] = els[i][1];
}
else if (l > 1)
for (i = 0; i < Nat; i++)
{
// iexp(kx[0]) = iexp(kx[0]) * iexp(kx[1])
x = elc[i][0];
elc[i][0] = x * elc[i][1] - els[i][0] * els[i][1];
els[i][0] = els[i][0] * elc[i][1] + x * els[i][1];
}
for (m = mmin; m < ky; m++)
{
rky = m * twopi * rb;
// iexp(kx*x[i]) * iexp(ky*y[i])
if (m >= 0)
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][m] - els[i][0] * ems[i][m];
lms[i] = els[i][0] * emc[i][m] + ems[i][m] * elc[i][0];
}
else // m :
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][-m] + els[i][0] * ems[i][-m];
lms[i] = els[i][0] * emc[i][-m] - ems[i][-m] * elc[i][0];
}
for (n = nmin; n < kz; n++)
{
rkz = n * twopi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < rkcut2) //
{
// (q[i]*iexp(kr[k]*r[i])) -
sumC = 0; sumS = 0;
if (n >= 0)
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][n] - lms[i] * ens[i][n]);
cks[i] = ch * (lms[i] * enc[i][n] + lmc[i] * ens[i][n]);
sumC += ckc[i];
sumS += cks[i];
}
else // :
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][-n] + lms[i] * ens[i][-n]);
cks[i] = ch * (lms[i] * enc[i][-n] - lmc[i] * ens[i][-n]);
sumC += ckc[i];
sumS += cks[i];
}
//
akk = exp(rk2 * elec->mr4a2) / rk2;
eng += akk * (sumC * sumC + sumS * sumS);
for (i = 0; i < Nat; i++)
{
x = akk * (cks[i] * sumC - ckc[i] * sumS) * C * twopi * 2 * rvol;
fxs[i] += rkx * x;
fys[i] += rky * x;
fzs[i] += rkz * x;
}
}
} // end n-loop (over kz-vectors)
nmin = 1 - kz;
} // end m-loop (over ky-vectors)
mmin = 1 - ky;
} // end l-loop (over kx-vectors)
engElec2 = eng * * twopi * rvol;
}
Einige Erklärungen für den Code: Die Funktion berechnet den komplexen Exponenten (in den Kommentaren zum Code wird er als iexp bezeichnet, um die imaginäre Einheit aus den Klammern zu entfernen) aus dem Vektorprodukt des k-Vektors und dem Radiusvektor des Partikels für alle k-Vektoren und für alle Partikel. Dieser Exponent wird mit der Teilchenladung multipliziert. Als nächstes wird die Summe solcher Produkte für alle Teilchen berechnet (die interne Summe in der Formel für E rec ), in Frenkel als Ladungsdichte und in Blinov als Strukturfaktor. Auf der Grundlage dieser Strukturfaktoren werden dann die auf die Partikel einwirkenden Energien und Kräfte berechnet. Die Komponenten von k-Vektoren (2π * l / a, 2π * m / b, 2π * n / c) sind durch drei ganze Zahlen l , m und n gekennzeichnet, die in Zyklen bis zu benutzerdefinierten Grenzwerten ausgeführt werden. Die Parameter a, b und c sind die Dimensionen des simulierten Systems in den Dimensionen x, y bzw. z (die Schlussfolgerung ist für ein System mit einer rechteckigen Parallelepiped-Geometrie richtig). Im Code entsprechen 1 / a , 1 / b und 1 / c den Variablen ra , rb und rc . Arrays für jeden Wert werden in zwei Kopien dargestellt: für den Real- und den Imaginärteil. Jeder nächste k-Vektor in einer Dimension wird iterativ aus dem vorherigen erhalten, indem der vorherige mit einem Komplex multipliziert wird, um den Sinus nicht jedes Mal mit dem Cosinus zu zählen. Die Arrays emc / s und enc / s werden für alle m ausgefülltund n , und das Array elc / s setzt den Wert für jedes l > 1 in den Nullindex von l , um Speicher zu sparen.
Zum Zwecke der Parallelisierung ist es vorteilhaft, die Reihenfolge der Zyklen "umzukehren", so dass der äußere Zyklus über die Partikel läuft. Und hier sehen wir ein Problem - diese Funktion kann nur parallelisiert werden, bevor die Summe über alle Teilchen berechnet wird (Ladungsdichte). Weitere Berechnungen basieren auf diesem Betrag und werden erst berechnet, wenn alle Threads ihre Arbeit beendet haben. Sie müssen diese Funktion also in zwei Teile aufteilen. Der erste berechnet die Ladungsdichte und der zweite berechnet die Energie und Kräfte. Beachten Sie, dass die zweite Funktion wieder die Menge q i benötigtiexp (kr) für jedes Teilchen und für jeden k-Vektor, berechnet im vorherigen Schritt. Und hier gibt es zwei Ansätze: entweder neu berechnen oder sich daran erinnern.
Die erste Option benötigt mehr Zeit, die zweite mehr Speicher (Anzahl der Partikel * Anzahl der k-Vektoren * sizeof (float2)). Ich entschied mich für die zweite Option:
__global__ void recip_ewald(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the first part : summ (qiexp(kr)) evaluation
{
int i; // for atom loop
int ik; // index of k-vector
int l, m, n;
int mmin = 0;
int nmin = 1;
float tmp, ch;
float rkx, rky, rkz, rk2; // component of rk-vectors
int nkx = md->nk.x;
int nky = md->nk.y;
int nkz = md->nk.z;
// arrays for keeping iexp(k*r) Re and Im part
float2 el[2];
float2 em[NKVEC_MX];
float2 en[NKVEC_MX];
float2 sums[NTOTKVEC]; // summ (q iexp (k*r)) for each k
extern __shared__ float2 sh_sums[]; // the same in shared memory
float2 lm; // temp var for keeping el*em
float2 ck; // temp var for keeping q * el * em * en (q iexp (kr))
// invert length of box cell
float ra = md->revLeng.x;
float rb = md->revLeng.y;
float rc = md->revLeng.z;
if (threadIdx.x == 0)
for (i = 0; i < md->nKvec; i++)
sh_sums[i] = make_float2(0.0f, 0.0f);
__syncthreads();
for (i = 0; i < md->nKvec; i++)
sums[i] = make_float2(0.0f, 0.0f);
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
ik = 0;
for (i = id0; i < N; i++)
{
// save charge
ch = md->specs[md->types[i]].charge;
el[0] = make_float2(1.0f, 0.0f); // .x - real part (or cos) .y - imagine part (or sin)
em[0] = make_float2(1.0f, 0.0f);
en[0] = make_float2(1.0f, 0.0f);
// iexp (ikr)
sincos(d_2pi * md->xyz[i].x * ra, &(el[1].y), &(el[1].x));
sincos(d_2pi * md->xyz[i].y * rb, &(em[1].y), &(em[1].x));
sincos(d_2pi * md->xyz[i].z * rc, &(en[1].y), &(en[1].x));
// fil exp(iky) array by complex multiplication
for (l = 2; l < nky; l++)
{
em[l].x = em[l - 1].x * em[1].x - em[l - 1].y * em[1].y;
em[l].y = em[l - 1].y * em[1].x + em[l - 1].x * em[1].y;
}
// fil exp(ikz) array by complex multiplication
for (l = 2; l < nkz; l++)
{
en[l].x = en[l - 1].x * en[1].x - en[l - 1].y * en[1].y;
en[l].y = en[l - 1].y * en[1].x + en[l - 1].x * en[1].y;
}
// MAIN LOOP OVER K-VECTORS:
for (l = 0; l < nkx; l++)
{
rkx = l * d_2pi * ra;
// move exp(ikx[l]) to ikx[0] for memory saving (ikx[i>1] are not used)
if (l == 1)
el[0] = el[1];
else if (l > 1)
{
// exp(ikx[0]) = exp(ikx[0]) * exp(ikx[1])
tmp = el[0].x;
el[0].x = tmp * el[1].x - el[0].y * el[1].y;
el[0].y = el[0].y * el[1].x + tmp * el[1].y;
}
//ky - loop:
for (m = mmin; m < nky; m++)
{
rky = m * d_2pi * rb;
//set temporary variable lm = e^ikx * e^iky
if (m >= 0)
{
lm.x = el[0].x * em[m].x - el[0].y * em[m].y;
lm.y = el[0].y * em[m].x + em[m].y * el[0].x;
}
else // for negative ky give complex adjustment to positive ky:
{
lm.x = el[0].x * em[-m].x + el[0].y * em[-m].y;
lm.y = el[0].y * em[-m].x - em[-m].x * el[0].x;
}
//kz - loop:
for (n = nmin; n < nkz; n++)
{
rkz = n * d_2pi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < md->rKcut2) // cutoff
{
// calculate summ[q iexp(kr)] (local part)
if (n >= 0)
{
ck.x = ch * (lm.x * en[n].x - lm.y * en[n].y);
ck.y = ch * (lm.y * en[n].x + lm.x * en[n].y);
}
else // for negative kz give complex adjustment to positive kz:
{
ck.x = ch * (lm.x * en[-n].x + lm.y * en[-n].y);
ck.y = ch * (lm.y * en[-n].x - lm.x * en[-n].y);
}
sums[ik].x += ck.x;
sums[ik].y += ck.y;
// save qiexp(kr) for each k for each atom:
md->qiexp[i][ik] = ck;
ik++;
}
} // end n-loop (over kz-vectors)
nmin = 1 - nkz;
} // end m-loop (over ky-vectors)
mmin = 1 - nky;
} // end l-loop (over kx-vectors)
} // end loop by atoms
// save sum into shared memory
for (i = 0; i < md->nKvec; i++)
{
atomicAdd(&(sh_sums[i].x), sums[i].x);
atomicAdd(&(sh_sums[i].y), sums[i].y);
}
__syncthreads();
//...and to global
int step = ceil((double)md->nKvec / (double)blockDim.x);
id0 = threadIdx.x * step;
N = min(id0 + step, md->nKvec);
for (i = id0; i < N; i++)
{
atomicAdd(&(md->qDens[i].x), sh_sums[i].x);
atomicAdd(&(md->qDens[i].y), sh_sums[i].y);
}
}
// end 'ewald_rec' function
__global__ void ewald_force(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the second part : enegy and forces
{
int i; // for atom loop
int ik; // index of k-vector
float tmp;
// accumulator for force components
float3 force;
// constant factors for energy and force
float eScale = md->ewEscale;
float fScale = md->ewFscale;
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
for (i = id0; i < N; i++)
{
force = make_float3(0.0f, 0.0f, 0.0f);
// summ by k-vectors
for (ik = 0; ik < md->nKvec; ik++)
{
tmp = fScale * md->exprk2[ik] * (md->qiexp[i][ik].y * md->qDens[ik].x - md->qiexp[i][ik].x * md->qDens[ik].y);
force.x += tmp * md->rk[ik].x;
force.y += tmp * md->rk[ik].y;
force.z += tmp * md->rk[ik].z;
}
md->frs[i].x += force.x;
md->frs[i].y += force.y;
md->frs[i].z += force.z;
} // end loop by atoms
// one block calculate energy
if (blockIdx.x == 0)
if (threadIdx.x == 0)
{
for (ik = 0; ik < md->nKvec; ik++)
md->engCoul2 += eScale * md->exprk2[ik] * (md->qDens[ik].x * md->qDens[ik].x + md->qDens[ik].y * md->qDens[ik].y);
}
}
// end 'ewald_force' function
Ich hoffe, Sie verzeihen mir, dass ich Kommentare auf Englisch hinterlassen habe. Der Code ist praktisch der gleiche wie in der Serienversion. Der Code wurde sogar besser lesbar, da Arrays eine Dimension verloren: elc / s [i] [l] , emc / s [i] [m] und enc / s [i] [n] wurden zu eindimensionalen el , em und en , Arrays lmc / s und ckc / s - in die Variablen lm und ck (Dimension nach Partikeln ist verschwunden, da es nicht mehr für jedes Partikel gespeichert werden muss, das Zwischenergebnis wird im gemeinsamen Speicher akkumuliert). Leider trat sofort ein Problem auf: die Arrays em und enmusste statisch eingestellt werden, um keinen globalen Speicher zu verwenden und nicht jedes Mal dynamisch Speicher zuzuweisen. Die Anzahl der Elemente in ihnen wird durch die NKVEC_MX- Direktive (die maximale Anzahl von k-Vektoren in einer Dimension) in der Kompilierungsphase bestimmt, und zur Laufzeit werden nur die ersten nky / z-Elemente verwendet. Zusätzlich erschien ein End-to-End-Index für alle k-Vektoren und eine ähnliche Direktive, wodurch die Gesamtzahl dieser Vektoren NTOTKVEC begrenzt wurde . Das Problem tritt auf, wenn der Benutzer mehr k-Vektoren benötigt, als in den Anweisungen angegeben. Zur Berechnung der Energie wird ein Block mit einem Nullindex bereitgestellt, da es keine Rolle spielt, welcher Block diese Berechnung in welcher Reihenfolge durchführt. Beachten Sie, dass der in der Variablen akk berechnete WertDer Seriencode hängt nur von der Größe des simulierten Systems ab und kann in der Initialisierungsphase berechnet werden. In meiner Implementierung wird er für jeden k-Vektor im Array md-> exprk2 [] gespeichert . In ähnlicher Weise werden die Komponenten von k-Vektoren aus dem Array md-> rk [] entnommen . Hier könnte es notwendig sein, vorgefertigte FFT-Funktionen zu verwenden, da die Methode darauf basiert, aber ich habe immer noch nicht herausgefunden, wie es geht.
Nun wollen wir versuchen, etwas zu zählen, aber das gleiche Natriumchlorid. Nehmen wir zweitausend Natriumionen und die gleiche Menge Chlor. Lassen Sie uns die Ladungen als ganze Zahlen festlegen und beispielsweise Paarpotentiale aus dieser Arbeit entnehmen. Lassen Sie uns die Startkonfiguration zufällig einstellen und leicht mischen, Abbildung 2a. Wir wählen das Volumen des Systems so, dass es der Dichte des Speisesalzes bei Raumtemperatur (2,165 g / cm 3 ) entspricht. Beginnen wir dies alles für eine kurze Zeit (10'000 Schritte von 5 Femtosekunden) mit naiver Berücksichtigung der Elektrostatik nach dem Coulombschen Gesetz und unter Verwendung der Ewald-Summation. Die resultierenden Konfigurationen sind in den 2b bzw. 2c gezeigt. Es scheint, dass im Fall von Ewald das System etwas schlanker ist als ohne ihn. Es ist auch wichtig, dass die Gesamtenergiefluktuationen mit der Verwendung der Summation signifikant abgenommen haben.

Abbildung 2. Erstkonfiguration des NaCl-Systems (a) und nach 10'000 Integrationsschritten: naive Methode (b) und mit dem Ewald-Schema (c).
Anstelle einer Schlussfolgerung
Es ist zu beachten, dass die in der Figur erhaltene Struktur nicht dem NaCl-Kristallgitter entspricht, sondern dem ZnS-Gitter, aber dies ist bereits eine Beschwerde über Paarpotentiale. Die Berücksichtigung der Elektrostatik ist für die Modellierung der Molekulardynamik sehr wichtig. Es wird angenommen, dass es die elektrostatische Wechselwirkung ist, die für die Bildung von Kristallgittern verantwortlich ist, da sie in großen Entfernungen wirkt. Aus dieser Position ist es allerdings schwierig zu erklären, wie Substanzen wie Argon beim Abkühlen kristallisieren.
Neben der erwähnten Ewald-Methode gibt es auch andere Methoden zur Berücksichtigung der Elektrostatik, siehe zum Beispiel diese Übersicht .