
Die Optimierung des Geschäftsbetriebs ist in den allermeisten Fällen mit der Verwendung der linearen Programmiermethode verbunden. Die Methode ist ziemlich einfach. Darüber hinaus gibt es einen Satz über die Existenz und Einzigartigkeit der Lösung.
In der Praxis ist jedoch nicht alles ganz einfach.
Das erste Problem ist die Nichtlinearität der Bedingungen der realen Welt. Damit die lineare Programmiermethode anwendbar ist, müssen sie linearisiert werden. Es gibt Möglichkeiten, die Nichtlinearität durch lineare Gleichungen und Ungleichungen plausibel festzulegen, indem neue Variablen eingeführt, Gewichtskoeffizienten festgelegt usw. werden. Bei der Lösung von Produktionsproblemen ist es in diesem Fall erforderlich, mit einer großen Anzahl von Variablen und dementsprechend Gleichungen (Ungleichungen) zu arbeiten.
In der Theorie der Lösung extremer Probleme gibt es einen Satz über die Stabilität von Lösungen für lineare Programmierprobleme. Demnach ist die Lösung nur dann stabil, wenn der Bereich des Problems konvex ist. Bei einer großen Anzahl von Variablen und Ungleichungen ist es nicht möglich festzustellen, ob der Bereich des Problems konvex ist. Darüber hinaus ist die Wahrscheinlichkeit einer Nichtkonvexität hoch.
Wenn das Problem nicht stabil ist, werden abhängig vom Startpunkt des Durchlaufens der Eckpunkte unterschiedliche Ergebnisse erhalten.
Zweites Problem- Einschränkung der Variablen von unten (x> h> 0). Jede Implementierung eines linearen Programmierverfahrens liefert immer einen x-Wert ungleich Null. Wenn x genau gleich h ist, bedeutet dies, dass der Wert der Variablen x im Wesentlichen Null sein sollte. In der Praxis sind solche „fiktiven“ Volumina (Methode Kurtosis) über „sinnvolle“ Variablen verteilt. Die Konsequenz dieser Praxis ist die Erosion des Konzepts einer optimalen Lösung, was besonders wichtig ist, wenn eine solche Lösung eine von vielen in der Entscheidungskette ist.
Das dritte Problem ist das Management. Die lineare Programmiermethode liefert nur ein Ergebnis. Und wie kann man Ergebnisse betrachten, die nahezu optimal sind? In der resultierenden Lösung ist beispielsweise die Lieferantenbewertung schlecht. Wie man versteht, ob es enge Lösungen gibt, aber für zuverlässige Lieferanten.
Transportaufgabe
Das Beispiel entspricht einem transportlinearen Programmierproblem.
Es gibt 5 Transportunternehmen (die Aufgabe wurde für den Transport von Kohle festgelegt), die zwei Tarifberechnungen haben. Tarifgrenzen und Tarife selbst können geändert werden (sie werden parametrisch festgelegt).

Der Transport wird als Punkt-zu-Punkt (gemäß der akzeptierten Methode für den Kohletransport) und Volumen angegeben.
Gesamtansicht der Schnittstelle.

Transportauftragsbereich.
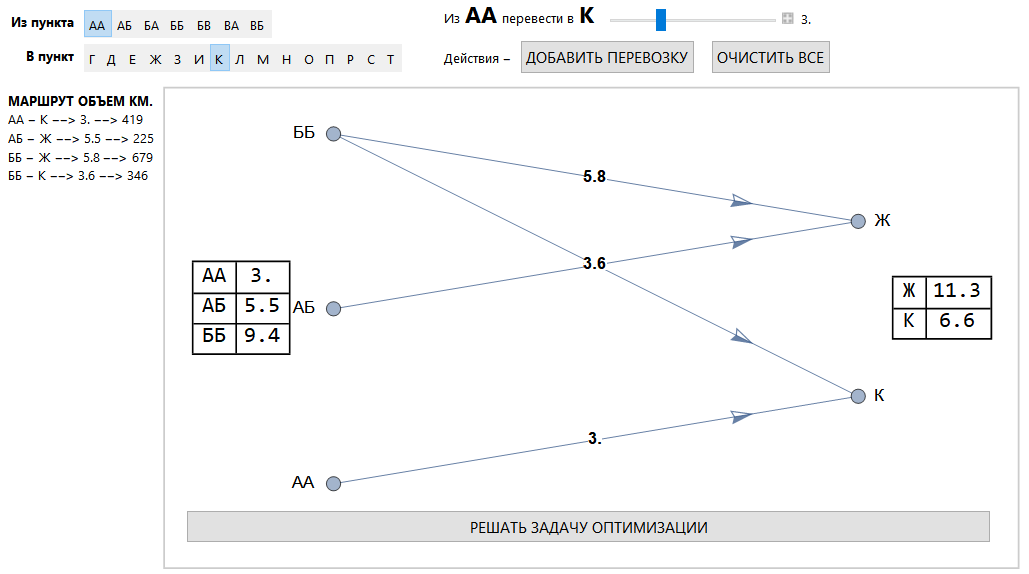
Cluster-Lösungsmethode
Anstelle eines linearen Programmierproblems wird eine Gruppe von Problemen gelöst, deren Anzahl allen möglichen Tarifkombinationen entspricht. In der obigen Sendung gibt es 127 davon (zweiter Wert im oberen linken Rechteck).

Die optimalen Lösungen werden aus dem Satz der verbleibenden korrekten Probleme ausgewählt. Jede Aufgabe bietet eine optimale Lösung für eine bestimmte Tarifkombination. Die oben vorgestellten Lösungen bilden einen bestimmten Bereich von Maxima.
Warum die Cluster-Methode gut ist:
- Verständnis der Stabilität der Lösung erscheint.
- Es gibt keine „fiktiven“ Volumina für von unten begrenzte Variablen, da es eine andere Kombination gibt, bei der eine solche Bedingung fehlt (da eine solche Variable fehlt).
- subjektive Bedingungen (Bewertungen, Präferenzen) können unter Verwendung der linearen Standardprogrammiermethode eingeführt werden.
Bei einer größeren Anzahl von Sendungen haben wir das folgende Bild (Fragment).
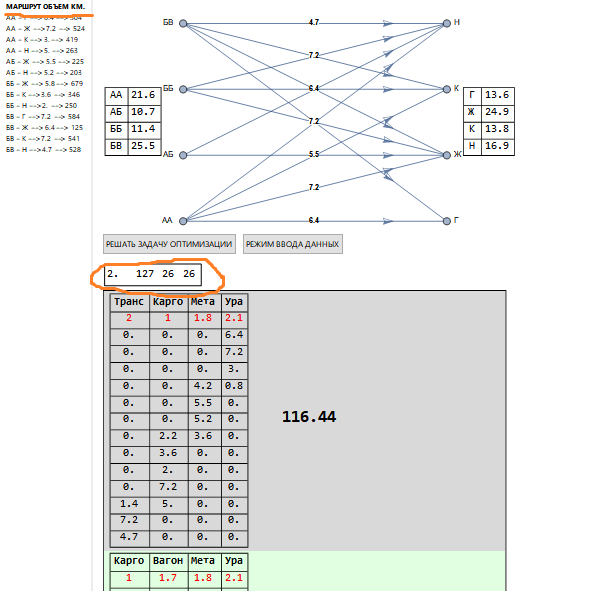
In der oberen linken Ecke des Rechtecks über den Lösungen (orange hervorgehoben) sind andere Werte als zuvor angegeben: 127 - Kombinationen (wie zuvor, die sich auf die Struktur der Tarifskalen beziehen), 26 - entsprechen der Anzahl der korrekten Probleme, die gelöst werden. Der verwendete Tarif wird unter dem Namen des Beförderers rot angezeigt, und die Transportspalten entsprechen der Liste der Routen (orange unterstrichen).
Es ist wichtig zu beachten, dass die verwendete Methode es Ihnen ermöglicht, das Ergebnis zu verstehen, ähnliche Lösungen zu bewerten und Ihre Berufserfahrung bei der Auswahl von Alternativen zu nutzen, wobei die Komplexität der Führung eines bestimmten Unternehmens berücksichtigt wird.