Clever Geek Handbook

Python-Tutorial-Projekt: Dijkstra-Algorithmus, OpenCV und UI (Teil 1)

Labyrinthe sind ein häufiges Rätsel für Menschen, aber sie sind ein interessantes Programmierproblem, das wir mit Methoden auf kürzestem Weg wie dem Dijkstra-Algorithmus lösen können.



Erinnern Sie sich an Dijkstras Algorithmus



Der Dijkstra-Algorithmus ist einer der beliebtesten graphentheoretischen Algorithmen. Es wird verwendet, um den kürzesten Pfad zwischen Knoten in einem gerichteten Graphen zu finden. Wir beginnen mit dem ursprünglichen Knoten und den bekannten Kantenlängen zwischen den Knoten.



Zuerst weisen wir allen Knoten den Abstand von der Quelle zu. Knoten s erhält den Wert 0, da es sich um die Quelle handelt. Der Rest erhält zunächst ∞ -Werte.



Bild



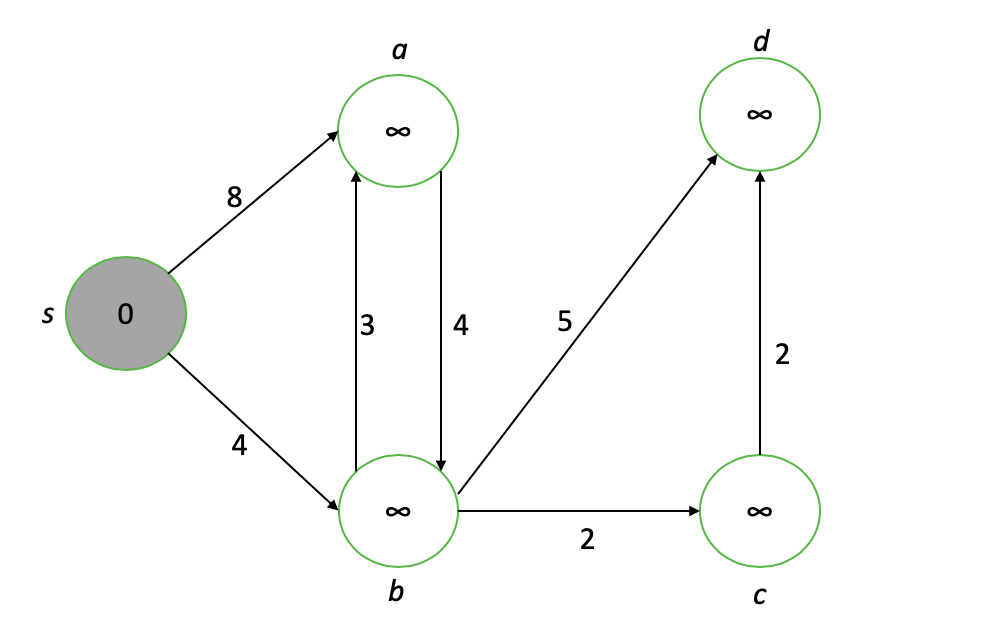
Unser interessierender Knoten ist der Rohknoten mit dem niedrigsten Wert (grau dargestellt), d. H. S. Zuerst "lockern" wir jeden benachbarten Scheitelpunkt zu unserem interessierenden Knoten und aktualisieren ihre Werte auf das Minimum ihres aktuellen Wertes oder den Wert des interessierenden Knotens plus der Länge der Verbindungskante ...



Bild



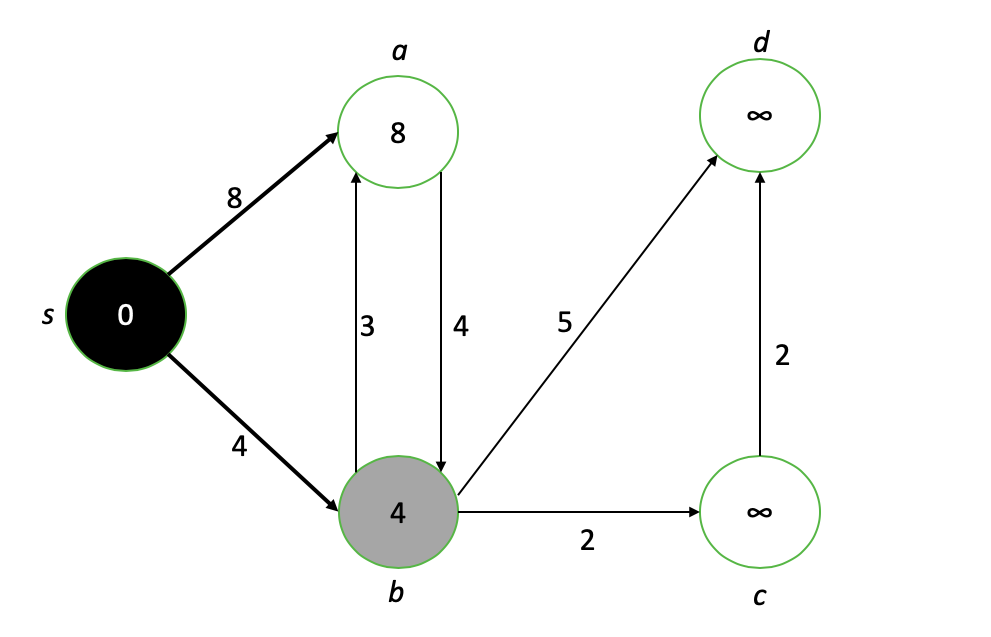
Knoten s ist jetzt vollständig (schwarz) und seine Nachbarn a und b haben neue Werte angenommen. Der neue interessierende Knoten ist b, daher wiederholen wir den Vorgang des „Schwächens“ der benachbarten Knoten von b und des Finalisierens des Werts des kürzesten Pfades für b.



Bild



Nachdem wir jeden Knoten durchlaufen haben, erhalten wir endlich ein Diagramm, das die kürzeste Pfadlänge von der Quelle zu jedem Knoten zeigt.



Bild



Bild



Bild



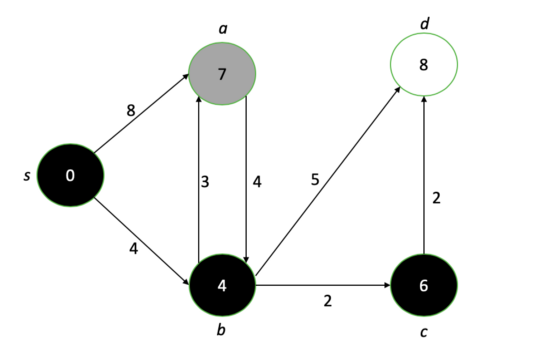
Unser letztes Diagramm nach dem Ausführen des Dijkstra-Algorithmus. Die Zahlen an jedem Knoten repräsentieren den kürzestmöglichen Abstand vom Quellknoten.



Konzeptualisierung von Labyrinthbildern.



Bild



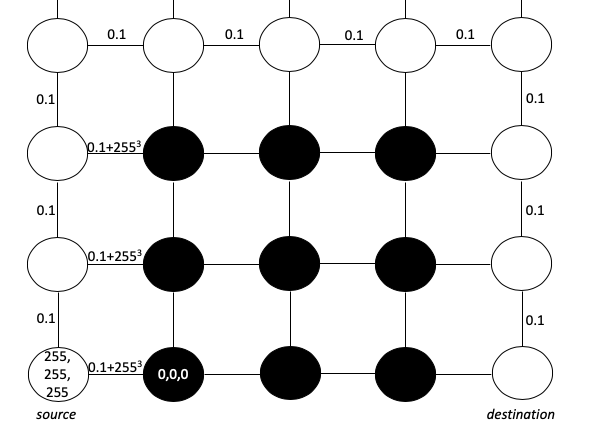
Wir können uns ein Bild als eine Matrix von Pixeln vorstellen. Jedes Pixel hat (der Einfachheit halber) einen Wert von RGB 0,0,0 (schwarz) oder 255,255,255 (weiß). Unser Ziel ist es, einen kürzesten Weg zu schaffen, der auf Weiß beginnt und nicht zu schwarzen Rändern führt. Um dieses Ziel darzustellen, können wir jedes Pixel als Knoten betrachten und Kanten zwischen benachbarten Pixeln mit Kantenlängen basierend auf der Differenz der RGB-Werte zeichnen. Wir werden die euklidische Quadratabstandsformel verwenden und 0,1 addieren, um sicherzustellen, dass es keine Pfadlänge 0 gibt - (Voraussetzung für den Dijkstra-Algorithmus):



Bild



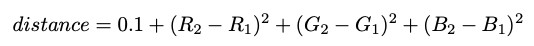
Diese Formel macht den Schnittabstand über die Labyrinthgrenze übermäßig groß. Wie wir sehen, führt der kürzeste Weg von der Quelle zum Ziel eindeutig um die Barriere herum und nicht durch diese hindurch.



Bild



Implementierung



Wir können OpenCV, eine beliebte Computer-Vision-Bibliothek für Python, verwenden, um Pixelwerte zu extrahieren und unsere Labyrinthbilder anzuzeigen. Definieren wir auch die Koordinaten unserer Start- und Endpositionen, indem wir unserem Labyrinth Punkte hinzufügen 



import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('maze.png') # read an image from a file using
cv2.circle(img,(5,220), 3, (255,0,0), -1) # add a circle at (5, 220)
cv2.circle(img, (25,5), 3, (0,0,255), -1) # add a circle at (5,5)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image
plt.show()


Bild


Wir erstellen eine Vertex-Klasse, mit deren Hilfe wir die Koordinaten verfolgen können. Wir möchten auch den übergeordneten Knoten verfolgen, damit wir den gesamten Pfad wiederherstellen können, sobald wir die Entfernungswerte gefunden haben. 



class Vertex:
    def __init__(self,x_coord,y_coord):
        self.x=x_coord
        self.y=y_coord
        self.d=float('inf') #current distance from source node
        self.parent_x=None
        self.parent_y=None
        self.processed=False
        self.index_in_queue=None


Wir müssen eine Scheitelpunktmatrix erstellen, die die zweidimensionale Anordnung der Pixel im Bild darstellt. Dies wird die Grundlage für den Dijkstra-Algorithmus sein. Wir unterhalten auch eine Warteschlange mit niedriger Priorität, um unverarbeitete Knoten zu verfolgen. 



def find_shortest_path(img,src,dst):
    pq=[] #min-heap priority queue
    imagerows,imagecols=img.shape[0],img.shape[1]
    matrix = np.full((imagerows, imagecols), None) 
    #access matrix elements by matrix[row][col]
    #fill matrix with vertices
    for r in range(imagerows):
        for c in range(imagecols):
            matrix[r][c]=Vertex(c,r)
            matrix[r][c].index_in_queue=len(pq)
            pq.append(matrix[r][c])
    #set source distance value to 0
    matrix[source_y][source_x].d=0
    #maintain min-heap invariant (minimum d Vertex at list index 0)
    pq = bubble_up(pq, matrix[source_y][source_x].index_in_queue)


Wir benötigen einige Hilfsfunktionen, um die Kanten und die Länge der Kanten zwischen den Eckpunkten zu ermitteln: 



#Implement euclidean squared distance formula
def get_distance(img,u,v):
    return 0.1 + (float(img[v][0])-float(img[u][0]))**2+(float(img[v][1])-float(img[u][1]))**2+(float(img[v][2])-float(img[u][2]))**2
#Return neighbor directly above, below, right, and left
def get_neighbors(mat,r,c):
    shape=mat.shape
    neighbors=[]
    #ensure neighbors are within image boundaries
    if r > 0 and not mat[r-1][c].processed:
         neighbors.append(mat[r-1][c])
    if r < shape[0] - 1 and not mat[r+1][c].processed:
            neighbors.append(mat[r+1][c])
    if c > 0 and not mat[r][c-1].processed:
        neighbors.append(mat[r][c-1])
    if c < shape[1] - 1 and not mat[r][c+1].processed:
            neighbors.append(mat[r][c+1])
    return neighbors


Jetzt können wir den Dijkstra-Algorithmus implementieren und allen Eckpunkten von Pixeln im Labyrinthbild Abstandswerte (d) zuweisen: 



while len(pq) > 0:
    u=pq[0] #smallest-value unprocessed node
    #remove node of interest from the queue
    pq[0]=pq[-1] 
    pq[0].index_in_queue=0
    pq.pop()
    pq=bubble_down(pq,0) #min-heap function, see source code 
    
    u.processed=True
    neighbors = get_neighbors(matrix,u.y,u.x)
    for v in neighbors:
        dist=get_distance(img,(u.y,u.x),(v.y,v.x))
        if u.d + dist < v.d:
            v.d = u.d+dist
            v.parent_x=u.x #keep track of the shortest path
            v.parent_y=u.y
            idx=v.index_in_queue
            pq=bubble_down(pq,idx) 
            pq=bubble_up(pq,idx)


Jetzt können wir die Funktion für den kürzesten Pfad aufrufen und die Lösung in unser Labyrinth zeichnen: 



img = cv2.imread('maze.png') # read an image from a file using opencv (cv2) library
p = find_shortest_path(img, (25,5), (5,220))
drawPath(img,p)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image on the screen 
plt.show()


Bild



Bild



Probieren wir andere Labyrinthe aus dem ganzen Internet aus.



Bild



Bild



Bild



Bild



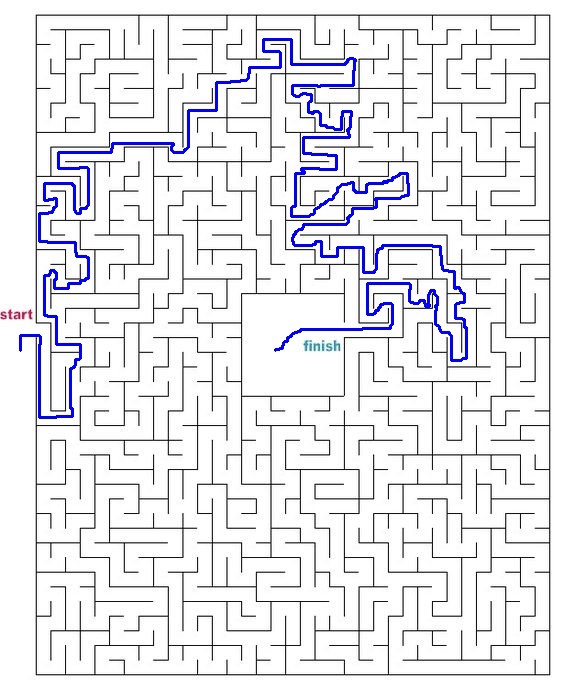
Der vollständige Quellcode ist auf GitHub verfügbar hier .



Fortsetzung: Python-Lernprojekt: 40 Zeilen Code-Oberfläche (Teil 2)



Bild



Erfahren Sie in unseren kostenpflichtigen Online-SkillFactory-Kursen, wie Sie einen hochkarätigen Beruf von Grund auf neu aufbauen oder Ihre Fähigkeiten und Gehälter verbessern können:










More articles:


All Articles