
Andere Artikel im Zyklus
Das Motiv für die Veröffentlichung derart detaillierter Texte zum AES-Standard besteht darin, die Möglichkeit zu bieten, sich mit ihm im Detail vertraut zu machen. Dies reicht aus, um nicht nur eine unabhängige Software-Implementierung des Verschlüsselungsalgorithmus zu entwickeln, sondern auch Algorithmen für mögliche kryptoanalytische Angriffe auf die Verschlüsselung zu erstellen, d. H. Zum Entschlüsseln von Verschlüsselungsgrammen, ohne den Schlüssel zu kennen .
Die im Netzwerk verfügbaren Veröffentlichungen erfüllen diese Ziele nicht und können von mir nicht für die Ausbildung von Fachleuten verwendet werden.
Eine der wichtigsten alten (oder sogar alten) Anforderungen für Chiffren besteht darin, einen offenen (für Studien zugänglichen) Verschlüsselungs- und Verschlüsselungsalgorithmus (Modi, Protokolle usw.) zu erstellen, der alle außer dem Chiffrierschlüssel enthält. Der Schlüssel ist etwas, das von allen streng vertraulich behandelt werden muss. In diesem Fall muss der Schlüssel nicht als "geheim" klassifiziert werden. Die Grenze einer solchen Bedingung ist, dass nur der Empfänger des Chiffriergramms den Schlüssel besitzt, er selbst muss ihn grundsätzlich festlegen.
Diese Bedingung ist für symmetrische Verschlüsselungssysteme nicht praktikabel. Und dies ist der grundlegende Unterschied zwischen asymmetrischen (Zwei-Schlüssel-) Systemen und symmetrischen Systemen, bei denen die Quelle des Informationsverlusts über den Schlüssel möglicherweise nicht die einzige ist. Es wurde bereits erwähnt, dass AES eine vereinfachte Version der RIJNDAEL-Verschlüsselung ist, und hier werden wir die Vollversion stellenweise verwenden.
AES (Key Schedule).
Die Auswahl eines Schlüssels beim Verschlüsseln einer Nachricht ist eine verantwortungsvolle Aufgabe. Der allgemeine Ansatz besteht darin, dass ein zufälliger binärer Vektor ausgewählt und für einen Schlüssel in einem mehrdimensionalen Vektorraum verwendet wird. Oft sind eine Reihe von Verschlüsselungsalgorithmen und Chiffren durch das Vorhandensein schwacher oder ungültiger Schlüssel gekennzeichnet, die entweder während der Entwicklung von Chiffren oder während ihres Betriebs während zusätzlicher Forschung identifiziert werden Algorithmen von Autoren oder Kryptographen Analysten und dementsprechend Veröffentlichungen darüber.
Dies führt wiederum zu Einschränkungen bei der Schlüsselgenerierung, was unerwünscht ist, da es dies kompliziert. Die mathematischen Grundlagen für die Verschlüsselung sind den mathematischen Grundlagen für die Generierung von Schlüsseln sehr ähnlich, und Sie können sie hier ausführlich lesen .
Der gewählte Binärvektor wird als Chiffrierschlüssel bezeichnet und in ein "Quadrat" von 4x4 = 16 Bytes konvertiert. Als nächstes werden daraus runde Schlüssel unter Verwendung von zwei speziellen Verfahren gebildet, die in den Verschlüsselungs- / Entschlüsselungsprozessen verwendet werden, die hier ausführlich beschrieben werden .
Eine Prozedur wird als Schlüsselerweiterung bezeichnet, die andere als runde Schlüsselauswahl. Der ausgewählte zufällige Zufallsvektor mit fester Länge wird erweitert. Es ist auch wichtig, die Wahl eines Zufallszahlengenerators sorgfältig zu prüfen, um ihn zu testen und zu genehmigen.
Schlüsselerweiterung
Die Bedeutung des Erweiterns des ursprünglichen (ausgewählten) Schlüssels besteht darin, ihn in Blöcke (jeweils 32 Bit) aufzuteilen und daraus für jede Runde einen Satz neuer Blöcke gleicher Länge zu generieren.
Lassen Sie also den ausgewählten (128-Bit) Chiffrierschlüssel AES = 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c für Nk = 4, der in Blöcken von 4 Bytes dargestellt wird und dessen anfängliche runde Erweiterung w [0 ist ] = 2b7e1516; w [1] = 28aed2a6; w [2] = abf71588; w [3] = 09cf4f3c. Das Symbol w [i] in der QC-Tabelle, i = 0 (1) 43, bezeichnet eine Spalte von 4 Bytes des runden Schlüssels.
Eine Verschlüsselungssitzung ist die Vorbereitung und algorithmische Transformation einer Nachricht, z. B. eines Briefes. Der Text des Buchstabens in Bitdarstellung ist in Blöcke fester Länge Nb = 128, 192 oder 256 Bit unterteilt. Im AES-Standard beträgt die Blocklänge nur 128 Bit.
Dann wird jeder Block durch ein Quadrat oder (Rechteck mit 4 Zeilen) dargestellt und separat für eine feste Anzahl von Runden Nr = Nr (Nb, Nk) verschlüsselt, was eine Funktion von zwei Variablen ist: der Länge des Blocks Nb und der Länge des Schlüssels Nk, die unabhängig voneinander Werte annehmen können 128, 192, 256 Bit.
Die Wahl des Verschlüsselungsschlüssels legt keine Einschränkungen für die Bitfolge selbst fest. Jede der Nr-Runden verwendet ihren eigenen vorgeformten oder direkt berechneten Rundenschlüssel {w [i]}.
Rundschlüssel werden aus dem Verschlüsselungsschlüssel mithilfe eines speziellen Algorithmus generiert, der das Verfahren zur Schlüsselerweiterung und das Verfahren zur Auswahl des Rundschlüssels umfasst. Es ist nicht akzeptabel, runde Schlüssel direkt anzugeben und diese Verfahren zu umgehen.
Das Wesentliche und der Zweck des ersten Verfahrens besteht darin, einen bestimmten ursprünglichen Verschlüsselungsschlüssel in einen längeren, erweiterten Schlüssel (erweiterten Schlüssel) umzuwandeln. Die Gesamtzahl der Bits des erweiterten Schlüssels, aus denen runde Schlüssel ausgewählt werden, wird durch das Produkt K = Nk (Nr + 1) bestimmt - die Anzahl der Bits des Schlüsselblocks wird mit der Anzahl der um eins erhöhten Runden multipliziert.
Beispiel 1 . Sei Nb = Nk = 4, gegebene Blöcke mit einer Länge von 4 × 32 = 128 Bits, dann Nr = 10.
Die Länge K in Bits für den erweiterten Schlüssel ist K = 128 ∙ 11 = 1408 Bits.
Die zweite Prozedur (RoundKey-Auswahl) ist eine sequentielle Auswahl von 32 Nk, d. H. 4 32-Bit-Wörtern aus dem erweiterten Schlüssel, d. H. Der erste runde Schlüssel wird durch die anfänglich neu gebildeten Nk-Wörter dargestellt, der zweite runde Schlüssel wird durch die nächsten Nk-Wörter dargestellt, und so weiter bis zur letzten Runde.
Beispiel 2. Mit den gleichen Anfangsdaten (siehe vorheriges Beispiel) enthält die Gesamtlänge des erweiterten Schlüssels in Bytes Nk (Nr + 1) = 4 ∙ 11 = 44 Vier-Byte-Wörter W (i),
i = 0 (1) Nk (Nr + 1) - 1 Die Zeilen der QC-Tabelle sind durch natürliche Zahlen nummeriert. Die erste Zeile ist mit 4 nummeriert, da 4 Zeilen (mit 0,1,2,3 nummeriert) mit dem Chiffrierschlüssel nicht in der QC-Tabelle enthalten sind.
Tabelle Chiffrierschlüssel AES für alle 10 Runden (siehe Tabelle QC unten).
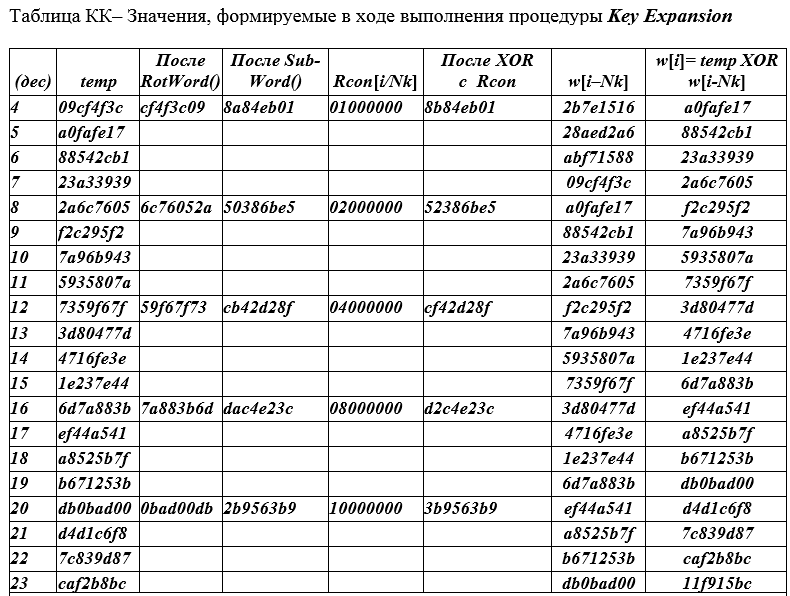
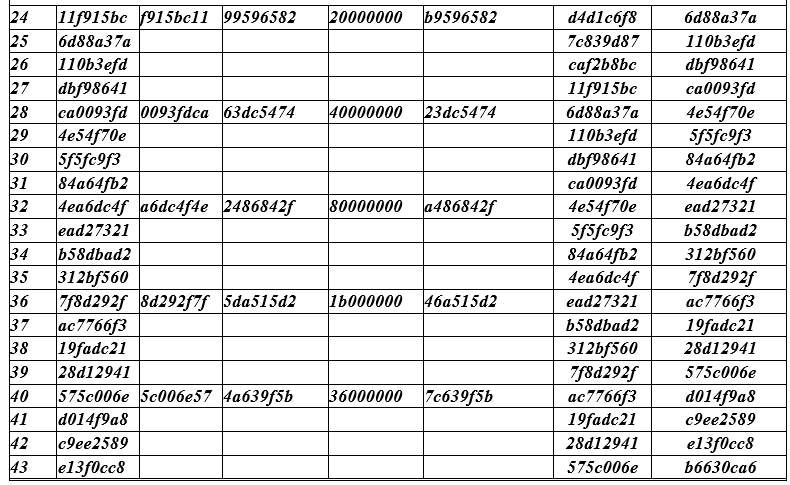
Die Zeilen der Tabelle sind in Gruppen unterteilt (jeweils 4 Zeilen). In jeder Gruppe werden alle Felder nur in einer obersten Zeile ausgefüllt. In den nächsten drei Zeilen werden nur die extremen Felder (links und rechts) ausgefüllt. Der linke Rand ( temp ) der nächsten und zwei nachfolgenden Zeilen enthält die Werte, die vom rechten Rand der darüber liegenden Zeile übernommen wurden.
Geben wir ein Beispiel für das Ausfüllen der ersten Zeile mit der Nummer i = 4 der QC-Tabelle. Linke Spalte - Die aktuellen Zeilennummern beginnen mit dem Wert (4), da die ersten 0,1,2,3-Werte nicht in der Tabelle enthalten sind. Im Allgemeinen läuft der Index (Zeilennummer) i über die Werte i = 0 (1) Nk (Nr + 1) -1 oder i = 0 (1) 43 in insgesamt 44 Wörtern mit 32 Bits.
Zur temporären SpalteDer Wert w [i-1] = 09cf4f3c wird platziert und durch Rotation (zyklische Verschiebung eines Bytes) RotWord () erhalten wir den Wert CF4F3C09, der in der 3. Spalte platziert wird. In der 4. Spalte wird das Ergebnis 8A84EB01 angezeigt, das die Bytes SubBytes der Werte aus der 3. Spalte ersetzt d.h. CF → 8A; 4F → 84; 3C → EB; 09 → 01 => 8A84EB01.
Jede 4. Zeile der Tabelle in der 5. Spalte ist mit dem Wert Rcon [i / Nk] gefüllt, einer Konstante, die nach der Formel Rcon (J) = 01000000, j = [i / Nk] = 2 j-1 = 2 0 = 1) berechnet wird. der Wert 01 00 00 00 wird aus 4-Byte-Wörtern geschrieben, von denen das erste Byte 2 0 = 1 ist, d.h. 0000 0001 2 sind die verbleibenden Bytes dieses 32-Bit-Wortes Null.
Das Feld in Spalte 6 enthält die Summe (XOR) der Felder des 4. und 5. 884EB01 + 01000000 = 8B84EB01;
Das Feld in Spalte 7 enthält W [i - Nk] = W [4 - 4] = W [0] = 2B7E1516;
Das Feld Spalte 8 enthält die Summe der Felder der Spalten 6 und 7 W [i = 4] = 884EB01 + 2B7E1516 = A0FAFE17;
Und jetzt im Detail und mit Details werden wir die genannten Verfahren betrachten.
Schlüsselerweiterungsverfahren
Betrachten wir im Detail das Verfahren zum Generieren eines erweiterten Schlüssels aus dem ursprünglichen Chiffrierschlüssel. Formal wird der erweiterte Schlüssel W durch eine Folge von Blöcken W [i], i = 0 (1) Nk (Nr + 1) -1, 4-Byte-Wörter (runde Schlüssel) beschrieben, die in der letzten Spalte der KK-Tabelle enthalten sind, in der das erste Nk 32-Bit enthalten ist Worte , um die Originalschlüssel repräsentieren, dh
W = {W [0], W [1], W [2], W [3], W [4], ..., W [K-1]}
anschließende i-ten Wörter werden rekursiv aus vorherigen Wörtern gemäß einem Ausdruck gebildet, in dem die Summation XOR ist.
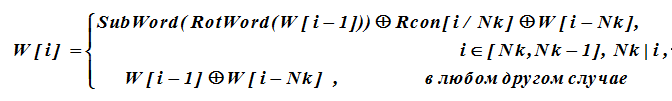 .
.
Für die Wörter W [i] des Schlüssels, dessen Index ein Vielfaches von Nk ist, werden die Werte von W [i-1] vor dem Ausführen der XOR-Operation einer zusätzlichen Transformation unterzogen. Diese Transformation wird wie folgt beschrieben.
Die Konvertierungsbeschreibung enthält Funktionen:
RotWord () - Bytezyklische Verschiebung des 32-Bit-Wortes a (0) a (1) a (2) a (3) gemäß der Regel
{a (0) a (1) a (2) a (3)} → {a (3) a (0) a (1) a (2)};
SubWord () - Bytersatz a (j) durch Elemente der S-Box der SubBytes () -Funktion, z. B. wird Byte (af) durch Bytes s (a, f) aus der S-Box ersetzt; Die Aktion ist dieselbe wie bei der Verarbeitung einer Nachricht,
Rcon [j] - der XOR-Term ist gleich 2 j-1 .

Hervorgehobene Positionen, die Vielfache von Nb sind, deren Werte mit den Funktionen SubWord (), RotWord (), Rcon () gebildet werden. Die Positionen W [0] –W [3] werden gemäß den angegebenen Anfangsdaten ausgefüllt, alle nachfolgenden werden durch das Verhältnis für W [i] berechnet.
Runde Tastenauswahl
Auswahl eines runden Schlüssels (RoundKeySelection). Für die aktuelle Runde mit der Nummer r. Der runde Schlüssel wird gewählt als {W [Nb (r) -1], ..., W [Nb (r + 1) - 1]},
r = 1 (1) Nr.
Hier stellen wir fest, dass der allgemeine Verschlüsselungsalgorithmus verschiedene Varianten der Variablensätze Nb, Nk, Nr. Für eine bestimmte Implementierung der festen Option kann sie stark vereinfacht werden. Der runde Schlüssel kann im laufenden Betrieb berechnet werden, was nicht viel Speicher benötigt, um die gesamte Sequenz W zu speichern. Sie können sich auf einen Puffer von Nk Wörtern beschränken.
Beispiel 3 . Lassen Sie uns die gegebenen theoretischen Sätze mit einem numerischen Beispiel erklären. Nach wie vor sei Nb = Nk = 4, Nr = 10. Der Chiffrierschlüssel wird in Form einer hexadezimalen Folge K = 2b7e1516 282ed2a6 abf71588 09cf4f3c angegeben

Die Architektur "Quadrat" und byteorientierte Berechnungen bestimmen die Form ihrer Darstellung in der folgenden Tabelle.
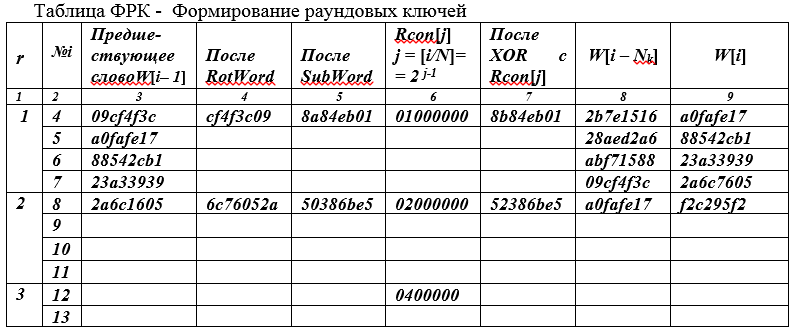
Die linke Spalte wurde der Tabelle hinzugefügt - die Nummer (r) der Runde.
In der ersten Zeile r = 1, i = 4 wird das vorhergehende Byte W [i-1] = W [3] in die dritte Spalte geschrieben, d. H. das letzte Byte des K-Chiffrierschlüssels. Da der Index i = 4 ein Vielfaches von Nk = 4 ist, schreiben wir in Spalte 6 (Rcon (J) = 01000000, j = [i / Nk] = 2 j-1 = 2 0 = 1) den Wert 01 00 00 00 4- x Byte Wort, dessen erstes Byte 2 0 = 1 ist, d.h. 0000 0001 sind die restlichen Bytes dieses 32-Bit-Wortes Null.
Geben Sie in der vierten Spalte der Tabelle die Werte aus der vorherigen Spalte ein, die jedoch zyklisch um 1 Byte nach links verschoben sind (Wortrotation - RotWord). Die fünfte Spalte enthält das Ergebnis der Bytersetzung der Werte der vorherigen Spalte durch die Werte der Bytes aus dem S-Block (SubWord-Funktion - Bytes ersetzen). Danach wird die mod2-Addition (XOR) des Inhalts der Spalten 5 und 6 durchgeführt, 8a84eb01 + 0100 0000 = 8b84eb01, und das Ergebnis der Summierung wird in Spalte 7 eingegeben.
In der binären Darstellung des Bytes 0000 0001 2 = 01 befinden sich die 16 niedrigstwertigen Bits rechts.
Spalte 8 enthält den Wert des Wortes W [i-Nk] = W [0] (für die erste Zeile ist dies der Wert des ersten (linken Bytes) 4-Byte-Wortes des Verschlüsselungsschlüssels W [0]), das durch die XOR-Operation 8b 84 eb 01+ hinzugefügt wird 2b 7e 15 16 = a0 fa fe 17 mit dem Inhalt von 7 Spalten. Das Summationsergebnis (Spalte 9) ist genau das erste von vier 4-Byte-Wörtern des Rundenschlüssels der ersten Runde.
Die anderen drei Wörter des Rundenschlüssels der ersten Runde werden ohne Verwendung der Funktion von zyklischer Verschiebung, Ersetzung und Rcon [j] gebildet, da ihre Zahlen keine Vielfachen von Nk sind. Der Inhalt von Spalte 9 wird in die dritte Spalte der nächsten Zeile der Tabelle übertragen.
Definition von Rcon [j]. Diese Prozedur wird nach einem speziellen Algorithmus durchgeführt, dessen Aktionen wir anhand von Beispielen veranschaulichen werden. Das Argument j der Funktion Rcon [j] ist eine Ganzzahl und wird durch den aktuellen Wert der Variablen i bestimmt - die Nummer des Schlüsselworts. Offensichtlich ist
j = 1, 2, 3, ... für i = Nk, 2Nk, 3Nk, ....
Da Nk in unserem Beispiel gleich 4 ist, haben wir ganzzahlige Werte j für i = 4, 8, 12. Ferner gilt für jede ganze Zahl j Rcon [j] = 2 j-1 = 1, 2, 4, 8, 16,….
Das Verdoppeln von Werten ist zulässig, solange Rcon [j] ein Element des GF (2 8 ) -Felds ist .
Für i> 32 erhalten wir j> 8. Werte außerhalb des Feldes müssen an das Feld zurückgegeben werden. Dies wird erreicht, indem die Polynomdarstellung der Elemente des Feldes Rcon [j] (modφ (x)) reduziert wird.
Beispiel 4. Sei i = 32, 36, 40. Dann ist j = 8, 9, 10. Diese Werte liegen außerhalb des Feldes. Wir bringen sie durch Reduktion modulo φ (x) ins Feld zurück und berechnen die erforderlichen Werte.
Bestimmen wir die entsprechenden Werte von Rcon [j]. Die Berechnungsergebnisse sind in einer Tabelle zusammengefasst.

Dies kann die Betrachtung der Schritte zum Erzeugen runder AES-Chiffrierschlüssel vervollständigen.