Wir machen uns weiterhin mit verschiedenen Heaps und Sortieralgorithmen vertraut, die diese Heaps verwenden. Heute haben wir den sogenannten Turnierbaum.
Die Hauptidee der Turniersortierung besteht darin, einen relativ kleinen (im Vergleich zum Hauptarray) Hilfsheap zu verwenden, der als Prioritätswarteschlange fungiert. In diesem Heap werden Elemente auf den niedrigeren Ebenen verglichen, wodurch kleinere Elemente (in diesem Fall haben wir einen MIN-HEAP-Baum) ansteigen und das aktuelle Minimum aus dem Teil der Array-Elemente, der in diesen Heap gefallen ist, zur Wurzel schwebt. Das Minimum wird an ein zusätzliches Array von "Gewinnern" übertragen, wodurch der Heap die verbleibenden Elemente vergleicht / verschiebt - und jetzt befindet sich ein neues Minimum in der Wurzel des Baums. Beachten Sie, dass bei einem solchen System das nächste Minimum einen höheren Wert hat als das vorherige - dann kann ein neu geordnetes Array von "Gewinnern" einfach zusammengestellt werden, wobei neue Minima einfach am Ende des zusätzlichen Arrays hinzugefügt werden.
EDISON .
, . , .
computer science ;-)
Das Verschieben der Minimums in ein zusätzliches Array führt dazu, dass im Heap für die nächsten Elemente des Hauptarrays Leerstellen angezeigt werden, wodurch alle Elemente in der Reihenfolge der Warteschlange verarbeitet werden.
Die hauptsächliche Subtilität ist, dass es neben den "Gewinnern" auch "Verlierer" gibt. Wenn einige Elemente bereits in das Array der "Gewinner" übertragen wurden und die unverarbeiteten Elemente kleiner als diese "Gewinner" sind, macht es zu diesem Zeitpunkt keinen Sinn, sie durch den Turnierbaum zu sichten. Das Einfügen dieser Elemente in das Array der "Gewinner" ist zu teuer (in Sie können ihnen nicht bereits ein Ende setzen, aber um sie am Anfang zu setzen, müssen Sie die bereits eingefügten Tiefs verschieben. Solche Elemente, die nicht in die Reihe der „Gewinner“ passen, werden an die Reihe der „Verlierer“ gesendet. Sie werden in einer der folgenden Iterationen durch den Turnierbaum geführt, wenn alle Aktionen für die verbleibenden Verlierer wiederholt werden.
Es ist nicht einfach, eine Implementierung dieses Algorithmus im Internet zu finden, aber eine klare und nette Implementierung in Ruby wurde auf YouTube gefunden. Java-Code wird auch im Abschnitt "Links" erwähnt, sieht dort jedoch nicht so lesbar aus.
#
require_relative "pqueue"
#
MAX_SIZE = 16
def tournament_sort(array)
# , ""
return optimal_tourney_sort(array) if array.size <= MAX_SIZE
bracketize(array) # , ""
end
#
def bracketize(array)
size = array.size
pq = PriorityQueue.new
#
pq.add(array.shift) until pq.size == MAX_SIZE
winners = [] # ""
losers = [] # ""
#
until array.empty?
# "" ?
if winners.empty?
# ""
winners << pq.peek
#
pq.remove
end
# , ""
if array.first > winners.last
pq.add(array.shift) #
else # ""
losers << array.shift # ""
end
# , ""
winners << pk.peek unless pk.peek.nil?
pq.remove #
end
# , - ?
until pq.heap.empty?
winners << pq.peek # ""
pq.remove #
end
# "" , , ,
# "" -
return winners if losers.empty?
# , ""
# ""
array = losers + winners
array.pop while array.size > size
bracketize(array) #
end
#
def optimal_tourney_sort(array)
sorted_array = [] #
pq = PriorityQueue.new
array.each { |num| pq.add(num) } # -
until pq.heap.empty? # -
sorted_array << pq.heap[0]
pq.remove #
end
sorted_array #
end
#
if $PROGRAM_NAME == __FILE__
#
shuffled_array = Array.new(30) { rand(-100 ... 100) }
#
puts "Random Array: #{shuffled_array}"
#
puts "Sorted Array: #{tournament_sort(shuffled_array)}"
endDies ist eine naive Implementierung, bei der nach jeder Unterteilung in "Verlierer" und "Gewinner" diese Arrays kombiniert werden und dann für das kombinierte Array alle Aktionen erneut wiederholt werden. Wenn die "verlierenden" Elemente zuerst im kombinierten Array angezeigt werden, werden sie beim Durchsuchen des Turnierstapels zusammen mit den "Gewinnern" sortiert.
Diese Implementierung ist recht einfach und intuitiv, kann aber nicht als effektiv bezeichnet werden. Die sortierten "Gewinner" durchlaufen den Turnierbaum mehrmals, was offensichtlich überflüssig ist. Ich nehme an, dass die zeitliche Komplexität hier log-quadratisch ist,
Multipath-Zusammenführungsoption
Der Algorithmus wird spürbar beschleunigt, wenn die geordneten Elemente, die das Sieb passieren, nicht wiederholt durch Turnierrennen geleitet werden.
Nachdem das ungeordnete Array in sortierte "Gewinner" und unsortierte "Verlierer" aufgeteilt wurde, wird der gesamte Vorgang nur für die "Verlierer" wiederholt. Bei jeder neuen Iteration wird eine Reihe von Arrays mit "Gewinnern" akkumuliert, und dies wird fortgesetzt, bis zu einem bestimmten Zeitpunkt keine "Verlierer" mehr vorhanden sind. Danach müssen nur noch alle Arrays von "Gewinnern" zusammengeführt werden. Da alle diese Arrays sortiert sind, erfolgt diese Zusammenführung zu minimalen Kosten.
In dieser Form findet der Algorithmus möglicherweise bereits eine nützliche Anwendung. Wenn Sie beispielsweise mit Big Data arbeiten müssen, werden im Verlauf des Prozesses mithilfe des Turnierhaufens Pakete mit geordneten Daten ausgegeben, mit denen Sie bereits etwas tun können, während alles andere verarbeitet wird.
Jedes der n Elemente des Arrays durchläuft den Turnierbaum nur einmal, was
Im Saisonfinale
Die Serie über Heap-Sortierungen ist fast abgeschlossen. Es bleibt zu sprechen über die effektivsten von ihnen.
Links
Tournament sort
Priority queue
Tournament sort in Java
The Theory Behind the The Theory Behind the z/Architecture Sort Assist Instructions
Using Tournament Trees to Sort
Tournament Sort Demo Ruby
Tournament Sort Visualization
Tournament Sort Data Structure UGC NET DS
Tournament Sort Algorithm — a Heapsort variant
:
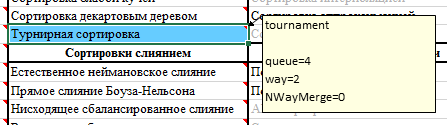
Die heutige Sortierung wurde der AlgoLab-Anwendung hinzugefügt, die sie verwendet. Aktualisieren Sie die Excel-Datei mit Makros.
In den Kommentaren zur Zelle mit dem Sortiernamen können Sie einige Einstellungen angeben.
Der variable Weg ist ein Mehrweg-Turnierbaum (nur für den Fall, dass dieser Baum nicht nur binär, sondern auch ternär, quaternär und pentarisch sein kann).
Die Warteschlangenvariable ist die Größe der ursprünglichen Warteschlange (die Anzahl der Knoten in der untersten Ebene des Baums). Da die Bäume voll sind, wenn beispielsweise mit way = 2 queue = 5 angegeben wird, wird die Größe der Warteschlange auf die nächste Zweierpotenz erhöht (in diesem Fall bis zu 8).
Variable NWayMerge nimmt den Wert 1 oder 0 an - es gibt an, ob eine Mehrweg-Zusammenführung verwendet werden soll oder nicht.