Was ist Musik in Bezug auf Mathematik? Was ist "la" oder "mi"? Wie genau Klänge gebildet werden, ist auf der Gitarre gut bekannt.
Sound "mi" (freies Klingen der 1. Saite), Sound "la" ( 1. Saite am 5. Bund geklemmt ). "La" ist 440 Hz. Was bedeutet 440 Hz? Das ist das 440-fache der Saite, die pro Sekunde vibriert. Der "mi" -Sound ist 5 Halbtöne niedriger als der "la" -Sound ( am 5. Bund geklemmt ).

Weitere 7 Halbtöne tiefer, ich werde wieder "mi" bekommen, d.h. Oktave. Warum wird sowohl der freie Klang der ersten Saite als auch der Klang der am 12. Bund festgeklemmten Saite als das gleiche Wort "mi" bezeichnet?

Es scheint uns, dass die gleiche Note gespielt wird. Tatsache ist, dass die Länge der Saite bis zu diesem Punkt ( "mi" am 12. Bund ) genau in zwei Hälften geteilt ist:
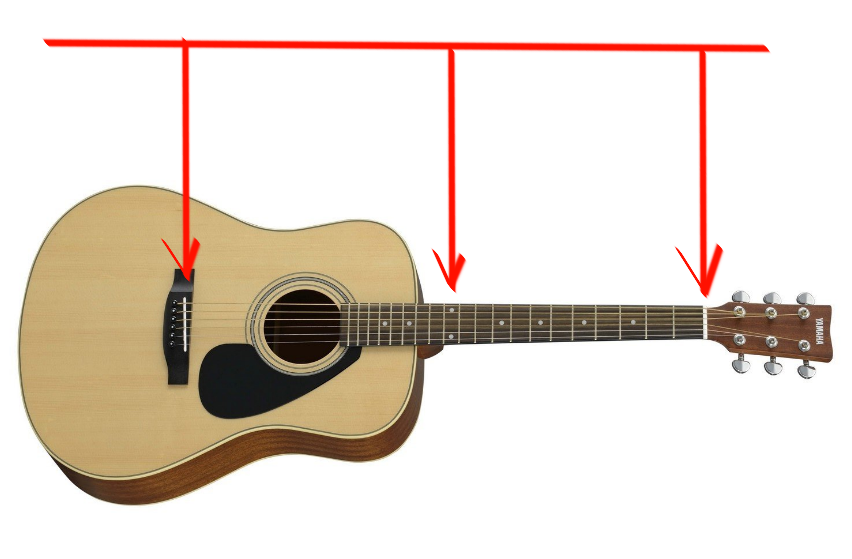
Dies bedeutet, dass die Schwingungen dieses Restes der Saite nach den Gesetzen der Physik doppelt so häufig sind wie die Schwingungen einer vollen Saite.
Jedes Mal, wenn ich die Saite zurücktrete und sie am nächsten Bund festklemme (die Teilung wird durch eine senkrechte Linie auf dem Griffbrett angezeigt ), steigt der Klang um einen Halbton, wie die Musiker sagen.
Beachten Sie, dass die Bünde auf dem Griffbrett unterschiedlich breit sind. Sie verjüngen sich allmählich, denn um die Frequenz um einen Halbton zu erhöhen, müssen Sie die Saitenlänge um eine bestimmte Anzahl von Malen reduzieren.
Worauf beziehe ich mich, wenn ich mich auf die Tatsache konzentriere, dass etwas "Ein" in etwas "In" übersetzt wird? Mathematiker würden sagen, dass es nur eine (unter bestimmten Bedingungen) Funktion gibt, bei der + zu x geht ( multiplizieren ). Und diese Funktion nennt man den Logarithmus.
Dies bedeutet, dass unsere Ohren, die die Saite verkürzen und den Klang eine bestimmte Anzahl von Malen anheben, als Anheben eines Halbtons wahrgenommen werden. Das heißt, jeder Bund verkürzt die Saite um die gleiche Anzahl von Malen, und unsere Ohren sagen, dass wir einen Halbton nach oben gehen, die Note "E" erreichen und eine Oktave erhalten. Unsere Hörorgane sind logarithmisch.
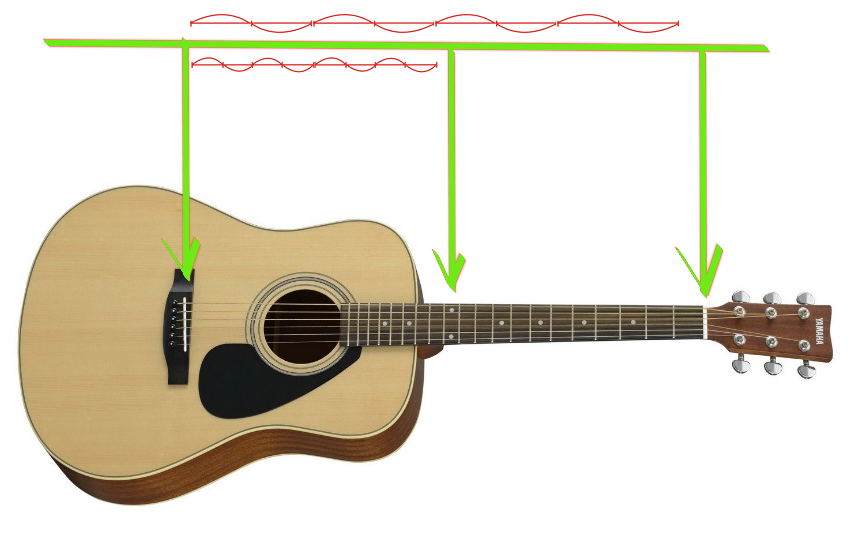
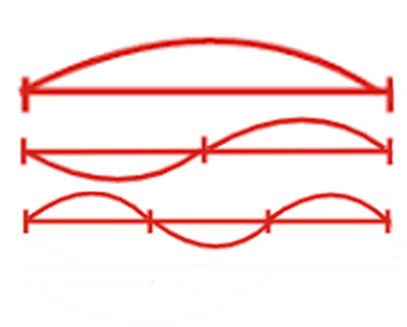
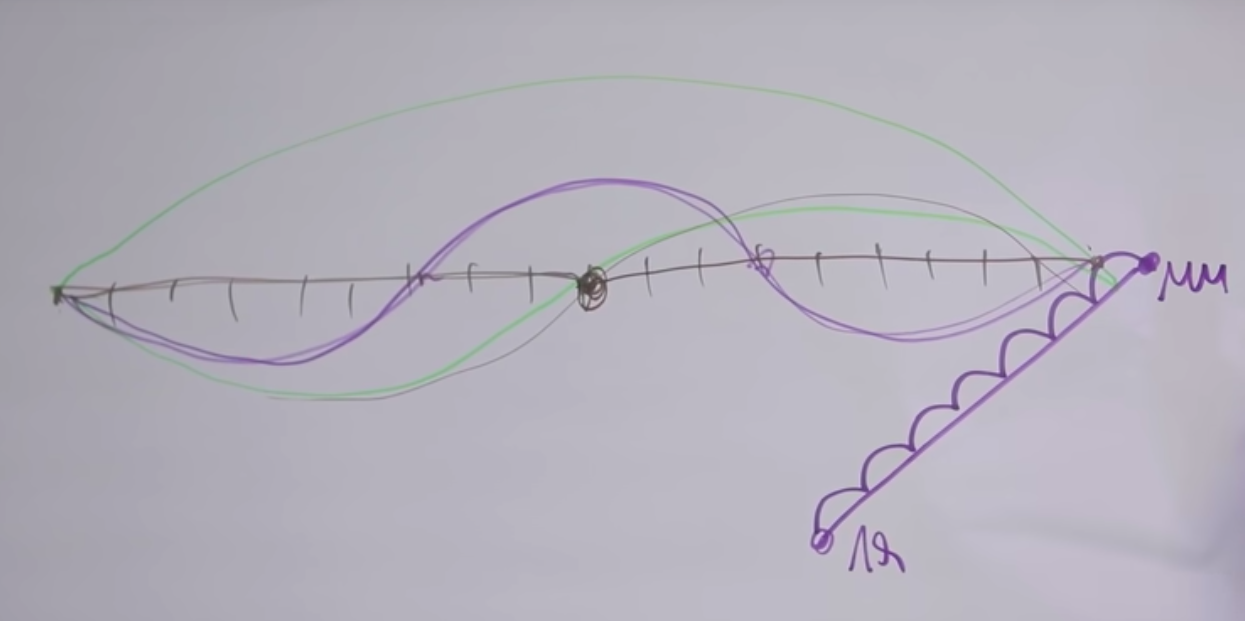
Wir sagen, dass "mi" und "mi" zweimal unterschiedlich sind, dies geht aus dem Klang hervor. Der obere Bogen ist in vollem Gange. Wenn wir es in der Mitte festklemmen, beginnt die Saite zu vibrieren, wie in der Grafik in der Mitte.
Warum sind die Klänge ähnlich? Tatsache ist, dass zusammen mit der Hauptschwingung der Saite tatsächlich die Schwingung derselben Saite bei allen Frequenzen auftritt, bei denen die Länge des Schwingungsabschnitts umgekehrt proportional zur Frequenz ist.
Wenn dementsprechend die Länge um eine ganze Zahl abnimmt, kann dementsprechend der entsprechende Oberton gehört werden. Der entsprechende Oberton wird durch die gegebene Saite realisiert. Wenn eine bestimmte Saite an diesen beiden Punkten teilweise fest vibriert ( unteres Diagramm ), ist ihr Ton dreimal höher.
Eine doppelte Frequenzerhöhung wird vom Ohr als dieselbe Note wahrgenommen. Alle Obertöne, die wir mehrmals teilen, d.h. Jede Unterteilung eines halben Segments ist sowohl eine automatische Unterteilung als auch ein großes Segment. Und nur einige Abteilungen eines großen Segments passen nicht in das Halbteilungsschema.
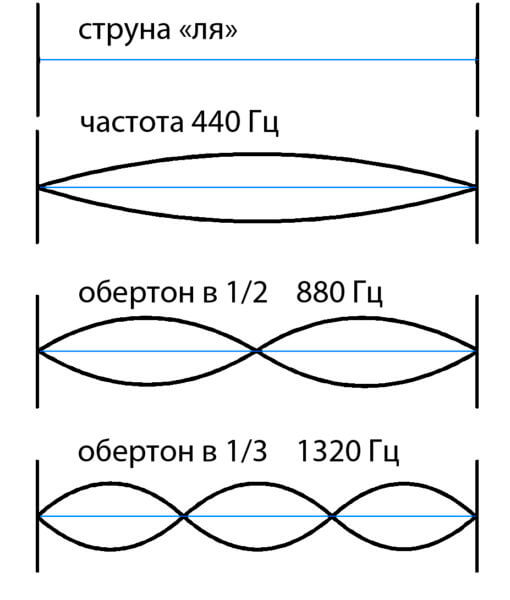
Wenn wir die geradzahligen oberen Töne für eine lange Saite nehmen, sind dies die oberen Töne für eine halb verkürzte Saite. Und absolut jeder verkürzte Klang einer kurzen Saite wird für eine lange klingen. Daher haben wir das Gefühl, dass alles, was wir hören, an diesen Punkten zusammenfällt, und wir nehmen es als eine Note wahr.
Es ist noch interessanter, dass es Noten gibt, die mehrere Halbtöne durchlaufen und von unseren Ohren als Konsonanz, Akkord, etwas, das dem Ohr gefällt, wahrgenommen werden, ohne unsere Ohren zu schneiden. Was sind diese Notizen?
Wenn Sie 7 Halbtöne aufnehmen, nehmen Sie die Note "A" und erhöhen Sie den Klang um 7 Halbtöne, bis zum nächsten "E", dann klingen diese beiden Noten gut.
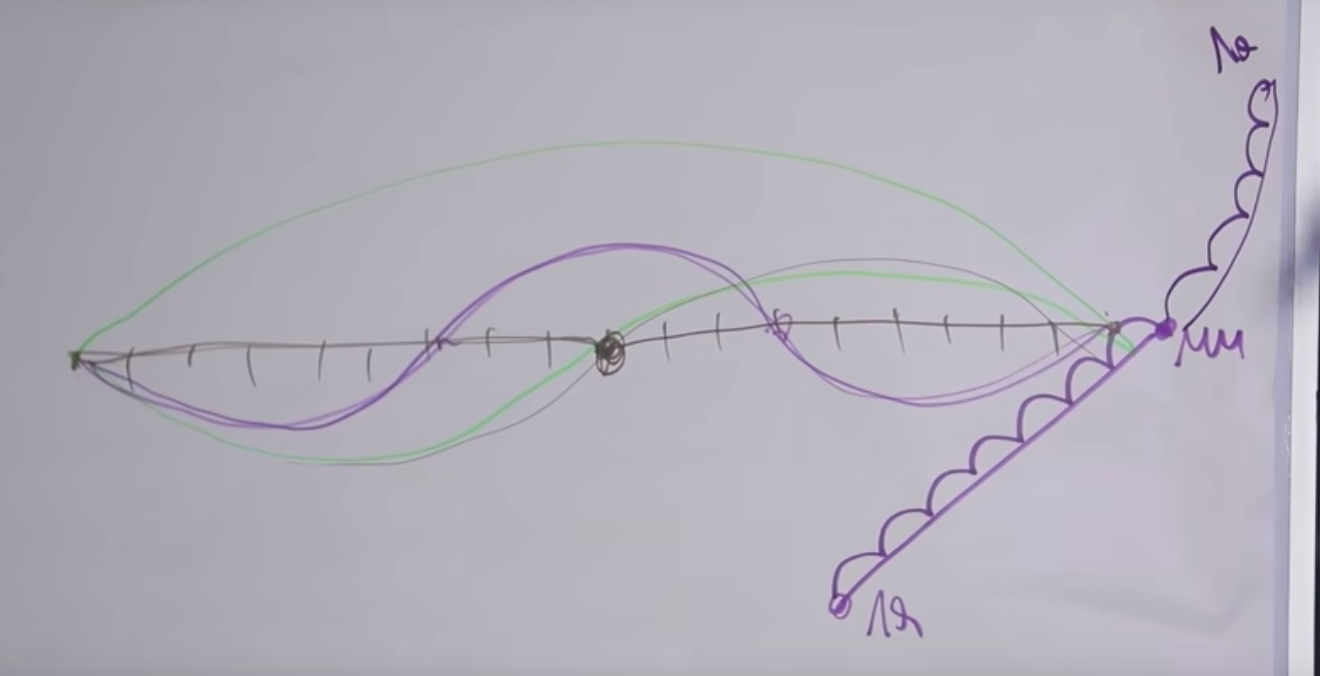
Wenn Sie weitere 5 Halbtöne zurücktreten, wird in der nächsten Oktave ein höheres "la" angezeigt. Aus irgendeinem Grund klingt dieses Intervall auch für uns angenehm. Lassen Sie uns alles herausfinden.
Wenn eine Erhöhung um 1 Halbton eine Erhöhung der Schwingungsfrequenz um eine bestimmte Anzahl von Malen ist, bezeichnen wir sie zunächst als x. Wenn Sie noch einen Halbton erhöhen müssen, gibt es bereits x * x, dh x 2 . Wenn ich es 12 Halbtöne (x 12 ) erhöht habe , sollte es genau 2 Mal erhöht werden. Wir erhalten die Gleichung x 12 = 2.
Daher bedeutet eine Erhöhung um 1 Halbton eine String-Kontraktion bei x = 12√2 oder, was gleich ist, Erhöhen der Schallfrequenz um 12 √2.
Und was haben "la" und "mi" damit zu tun? Warum klingen 7 Halbtöne melodisch? Erhöhen wir den Abschluss:
Was ist so angenehm, gut an dieser Zahl?
Irgendwann in der Antike wurden temperierte Claviers erfunden, eine genaue Aufnahme von Musik. Sie können es sehr gut auf der Gitarre sehen, Sie können es auch auf dem Klavier finden, es ist im Inneren versteckt, wenn Sie schauen, können Sie die Saiten sehen.
Jetzt ist diese Zahl sehr nahe an 3/2. Wenn Sie mit einem Taschenrechner rechnen, ist dieser sehr genau. Dies bedeutet, dass "mi" ungefähr 1,5-mal höher ist als das vorherige "la". Jene. Das Anheben von 7 Tönen entspricht einem 3/2-Anstieg, was bedeutet, dass viele obere Obertöne zusammenfallen.
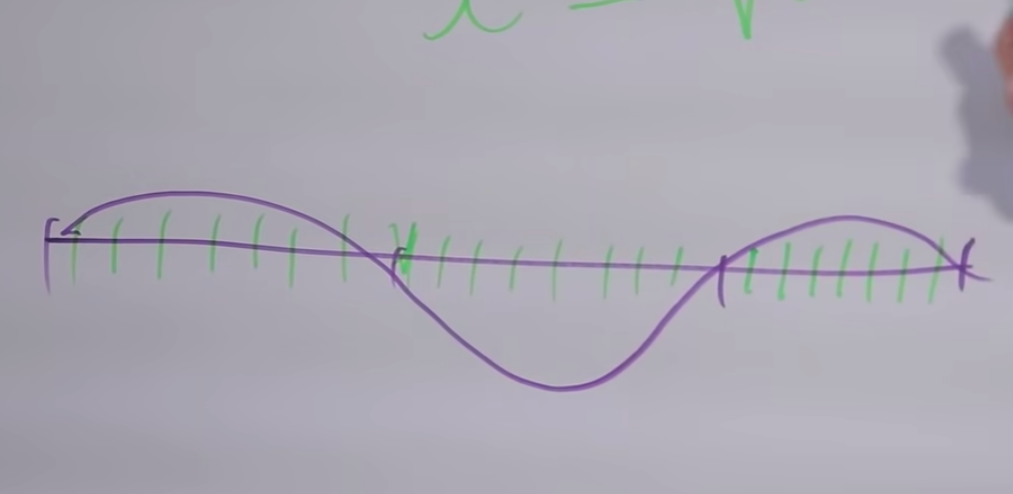
Denn jede Division durch eine Ganzzahl eines kleinen Segments ist eine Ganzzahldivision des gesamten Segments. Dementsprechend ist das Teilen des ursprünglichen Schnitts durch die Anzahl der Teile, ein Vielfaches von drei, die Division des kleinen Segments (⅓) und auch ⅔. Wenn wir ⅔ von der Länge verließen, d.h. erhöhte die Frequenz auf 3/2, wir stiegen um ungefähr 7 Halbtöne, wir werden viele gemeinsame Obertöne haben, es wird eine angenehme Konsonanz sein.
Das verbleibende 4/3 ist genau die 5 verbleibenden Halbtöne, 3/2 x 4/3 = 2, nur eine Oktave. Welches entspricht der Formel x71243. Der Wert liegt sehr nahe bei 4/3, aber nicht bei 100%. Diese Zahl ist irrational, kann nicht als Bruch geschrieben werden, sie kann nicht als Ganzzahl geteilt durch eine Ganzzahl geschrieben werden.
Ich habe gehört, dass es in Indien ein Instrument gibt ( Sitar), in dem die Oktave in 19 Teile unterteilt ist, d.h. Sie haben einen Halbton = 1/19 Oktave, 19x2.

Und schon mit großer Genauigkeit x121932, was bedeutet, wenn Sie auf einem solchen indischen Instrument 12 von 19 Segmenten zurücktreten, dann gibt es in dieser Konsonanz mehr übereinstimmende Obertöne, und dieses Intervall klingt wie ein Balsam für die Ohren.
Über Musik und Mathematik gibt es viele interessante Dinge zu sagen. Insbesondere wird ein Dur-Akkord wahrgenommen, wenn Sie einer Anfangsnote 4 Halbtöne hinzufügen und dann 3, d. H. 0 - 4 - 3. A-Moll, wenn Sie am Anfang 3 und dann 4 hinzufügen, d. H. 0 - 3 - 4. Die erste und letzte der drei Noten des Akkords sind "gleich", sie unterscheiden sich nur um 7 Halbtöne, aber der mittlere Klang erzeugt unsere Wahrnehmung der Konsonanz und stimmt in einem Moll- oder Dur-Modus.
Es scheint, dass Musik und Mathematik, was kann gemeinsam sein? Und es gibt so viele Gemeinsamkeiten, dass Mathematiker und Musiker oft miteinander kommunizieren. Außerdem verstehen Mathematiker Musiker sozusagen leicht, dass sie einen Halbton erfassen.
Mehrere nützliche Links:
- Musiktheorie für Geeks
- Notation wird nicht richtig gelehrt *
- Warum gibt es so viel Mathematik in der Musik?