Hallo Bewohner! Ein Koloss mit Lehmfüßen kann man als Programmierer bezeichnen, ohne eine Ausbildung in Informatik zu haben. Durch die sichere Beherrschung der Grundlagen können Sie das Rad nicht neu erfinden und effektive Lösungen in die Softwarearchitektur integrieren. All dies eliminiert Fehler und übermäßige Kosten für Tests und Refactoring.
Es spielt keine Rolle, ob Sie sich fehl am Platz fühlen, wenn andere Programmierer das ungefähre Limit besprechen. Selbst erfahrene Spezialisten machen Fehler, weil sie die Informatik vergessen haben.
Warum dieses Buch benötigt wird
Viele meiner (Autoren-) Kollegen kamen aus einer Vielzahl von Bereichen in den Beruf. Einige haben eine höhere Ausbildung in Informatik; andere studierten Fotografie, Mathematik oder absolvierten nicht einmal die Universität.
In den letzten Jahren habe ich festgestellt, dass Programmierer aus mehreren Gründen zunehmend darauf aus sind, Informatik zu lernen:
- gute Programmierer zu werden;
- Fragen zu Algorithmen während der Interviews zu beantworten;
- um ihre Neugier auf dem Gebiet der Informatik zu befriedigen oder endlich aufzuhören zu bedauern, dass sie einmal nicht die Gelegenheit hatten, dieses Fach zu beherrschen.
Dieses Buch ist für euch alle.
Viele finden hier Themen, die für sich genommen interessant sind. Ich habe versucht zu zeigen, in welchen realen (nicht akademischen) Situationen dieses Wissen nützlich sein wird. Nach dem Lesen dieses Buches möchte ich, dass Sie das gleiche Wissen wie nach dem Studium des Grundkurses Informatik erwerben und auch lernen, wie man es anwendet.
Einfach ausgedrückt, der Zweck dieses Buches ist es, Ihnen zu helfen, durch ein besseres Verständnis der Informatik ein erfahrener Programmierer zu werden. Ich kann 20 Jahre College-Unterricht und Berufserfahrung nicht in einem Buch zusammenfassen ... aber ich werde versuchen, mein Bestes zu geben. Ich hoffe, dass Sie hier mindestens ein Thema finden, zu dem Sie sagen können: „Ja, jetzt verstehe ich das“ und Wissen in Ihre Arbeit einbringen.
Was Sie in der Ausgabe nicht finden werden
Die Bedeutung des Buches besteht darin, dem Leser zu helfen, die Informatik besser zu verstehen und Wissen in der Praxis anzuwenden, und vier Jahre Studium überhaupt nicht vollständig zu ersetzen.
Insbesondere ist dies kein Beweisbuch. In der Tat werden im zweiten Band des Buches Beweismethoden betrachtet, aber Standardalgorithmen werden hier normalerweise ohne Beweise vorgestellt. Die Idee ist, dass der Leser über die Existenz dieser Algorithmen Bescheid weiß und lernt, wie man sie verwendet, ohne auf Details einzugehen. Als Korrekturbuch für Studenten und Doktoranden empfehle ich die Einführung in Algorithmen von Cormen, Leiserson, Rivest und Stein (Autoren werden normalerweise unter zusammengefasst) Abkürzung CLRS).
Dies ist auch kein Programmierbuch: Sie finden keine Richtlinien, wann int und wann double verwendet werden soll, oder eine Erklärung, was eine Schleife ist. Es wird erwartet, dass der Leser die Pseudocode-Listen verstehen kann, die zur Beschreibung der Algorithmen verwendet werden (alle Programme in diesem Buch sind in Pseudocode basierend auf der C-Sprache geschrieben). Der Zweck des Buches ist es, die Konzepte der Informatik mit Programmiertechniken zu verbinden, die dem Leser bereits vertraut sind.
10. Dynamische Programmierung
10.1. Problem mit fehlenden Feldern
Angenommen, auf einem n × n-Schachbrett fehlen mehrere Felder. Wie finde ich das größte k × k-Stück Brett ohne fehlende Felder?
Wenn Sie zuvor noch nicht mit einem solchen Problem konfrontiert waren, nehmen Sie sich ein paar Minuten Zeit, um eine Lösung zu schreiben und die Ausführungszeit Ihres Algorithmus zu bestimmen.
Angesichts dieses Problems habe ich Folgendes begründet. Jedes Schachbrettfeld kann zu vielen der größten Bereiche gehören, aber nur in einem davon kann es die obere linke Ecke sein. Wenn ich jedes Feld mit der Größe des größten intakten Bereichs markiere, von dem es die obere linke Ecke ist, entspricht das Feld mit der größten solchen Markierung dem gewünschten Bereich.
Angenommen, die Karte wird als n × n-Matrix dargestellt, in der jede Zelle 1 enthält, wenn das entsprechende Feld vorhanden ist, und 0, wenn es fehlt. Wenn der aktuelle Zellenwert 0 ist, fehlt das entsprechende Feld und kann nicht Teil eines zusammenhängenden Bereichs sein, sodass es nicht geändert werden muss. Wenn der Wert 1 ist, können wir ihn durch eine Zahl ersetzen, die um eins höher ist als der Mindestwert der drei Zellen unten und rechts.
Wir ändern jede Zelle der Matrix einmal, einschließlich der Überprüfung, ob der Wert der Zelle Null ist, der Überprüfung der Werte von bis zu drei weiteren Zellen und des Schreibens des neuen Zellenwerts. Jede dieser Operationen benötigt O (1) Zeit, also die Zeit, die benötigt wird, um das gesamte Schachbrett zu verarbeiten
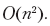
Beachten Sie, dass dies eine lineare und keine quadratische Ausführungszeit des Algorithmus ist - auf einem Schachbrett n (wir nehmen an, dass n die Gesamtzahl der Felder ist, und wir halten uns an die übliche Konvention, dass n die Menge der Eingabedaten ist) Felder (einige davon sind) abwesend), daher ist die vom Algorithmus insgesamt aufgewendete Zeit proportional zur Anzahl der Felder. Wenn wir die Größe des Schachbretts genauer als √ n × √ n bezeichnen, erhalten wir n Felder und die Gesamtausführungszeit ist O (n).
10.2. Arbeiten mit überlappenden Unteraufgaben
Der in diesem Abschnitt verwendete Ansatz wird als dynamische Programmierung bezeichnet. Es wird verwendet, wenn ein Problem in mehrere Unteraufgaben unterteilt werden kann, deren Lösung jeweils mehrmals verwendet wird. Dieser Ansatz unterscheidet sich vom Prinzip "Teilen und Erobern", wenn das Problem in Teilaufgaben unterteilt wird, die unabhängig voneinander gelöst werden. Bei dem Schachbrettproblem hing jedes Teilproblem von den Lösungen für drei andere Probleme ab, und die Lösungen für alle Teilprobleme wurden zur weiteren Verwendung gespeichert.
Die dynamische Programmierung erfolgt normalerweise durch Erstellen von Tabellen wie oben gezeigt. Dies bedeutet, ein Problem mit einem Bottom-up-Ansatz zu lösen, bei dem wir zunächst die kleinsten Teilprobleme lösen und uns nach oben arbeiten, bis wir zu einer Antwort kommen. Eine andere Methode ist die Memoisierung, bei der wir von oben nach unten gehen, Unterprobleme nach Bedarf lösen und die Ergebnisse zur Wiederverwendung zwischenspeichern. Das Erstellen von Tabellen ist die bevorzugte Option, wenn Sie jedes Teilproblem lösen müssen (in meinem Beispiel mit einem Schachbrett musste der größte intakte Bereich für jedes Feld des Bretts gefunden werden), da die Kosten dieser Methode geringer sind als beim Auswendiglernen. Wenn einige Unteraufgaben aus dem Lösungsbereich nicht gelöst werden müssen, können Sie mit Memoization nur die wirklich erforderlichen Unteraufgaben lösen.
Der entscheidende Punkt
Wenn beim Teilen und Erobern eine Aufgabe in mehrere unabhängige Unteraufgaben aufgeteilt wird, bedeutet dynamische Programmierung, dass eine Aufgabe in mehrere überlappende Unteraufgaben aufgeteilt wird. Die Lösung für jedes Teilproblem wird zur späteren Wiederverwendung zwischengespeichert.
10.3. Dynamische Programmierung und kürzeste Wege
Betrachten Sie das Problem, den kürzesten Pfad zu finden: Für ein bestimmtes Diagramm mit gewichteten Kanten müssen Sie einen Pfad von einem Knoten zu einem anderen finden, der die niedrigsten Kosten verursacht.
Definition Ein
kantengewichteter Graph ist ein Graph, in dem jede Kante ihr eigenes Gewicht (Kosten) hat. Die Kosten eines Pfades von einem Knoten zu einem anderen werden durch die Summe der Kosten aller durchquerten Kanten bestimmt.
Angenommen, wir finden einen Pfad zwischen den Knoten s und t, der den dritten Knoten v enthält. Dann muss der Pfad von s nach t den kürzesten Pfad von s nach v enthalten, da wir sonst dieses Segment durch einen kürzeren Pfad ersetzen und die Länge des kürzesten Pfades von s nach t verringern könnten, was der Anfangsbedingung widerspricht (dies ist Bellmans Optimalitätsprinzip).
( ) , . , . , .
, , .
Die Probleme, den kürzesten Weg zu finden, sind eindrucksvolle Beispiele für dynamische Programmierung, da die optimale Eigenschaft einer Unterstruktur intuitiv klar ist - es ist offensichtlich, dass der schnellste Weg von Punkt A nach Punkt C durch Punkt B auch der schnellste Weg von Punkt A nach Punkt B und von Punkt ist B bis Punkt C. Die Anzahl der auf diesem Prinzip basierenden Algorithmen umfasst die Bellman-Ford-Methode, die mit ihrer Hilfe den kürzesten Weg vom Startpunkt zu einem beliebigen Scheitelpunkt des Diagramms (oder von einem beliebigen Scheitelpunkt des Diagramms zum Endpunkt) und die Floyd-Warshall-Methode findet Der kürzeste Weg zwischen jedem Paar von Graphenscheitelpunkten wird berechnet. In beiden Fällen besteht die Idee darin, mit einer kleinen Teilmenge von Knoten in der Nähe der interessierenden Knoten zu beginnen und diese Menge schrittweise zu erweitern, indem die bereits gefundenen Knoten verwendet werden, um neue Entfernungen zu berechnen.
10.4.
10.4.1. Git merge
Eine weitere Aufgabe, die häufig zur Demonstration der dynamischen Programmierung verwendet wird, ist das Auffinden der längsten gemeinsamen Folge. Die Aufgabe besteht darin, für zwei gegebene Zeichenfolgen A und B die längste Sequenz zu finden, die in beiden Zeichenfolgen auftritt, während die Zeichenfolge beibehalten wird. Zeichen in Zeichenfolgen müssen nicht hintereinander stehen. Wenn beispielsweise A = {acdbef} und B = {babdef} ist, ist {adef} ihre gemeinsame Teilsequenz.
Beim Zusammenführen von Änderungen in Git (Zusammenführen) wird nach der größten gemeinsamen Teilsequenz für Master- und Arbeitszweige gesucht. Zeichen, die im Master vorhanden sind, aber nicht in der größten gemeinsamen Teilsequenz vorhanden sind, werden entfernt. Zeichen, die sich im Arbeitszweig befinden, sich jedoch nicht in dieser Teilsequenz befinden, werden dem Master hinzugefügt.
10.4.2. LATEX
Das LATEX-Dokumentvorbereitungssystem wird häufig zum Erstellen technischer Dokumente verwendet. Eine der Aufgaben des Schreibsystems besteht darin, den Text gleichzeitig nach rechts und links auszurichten. Dazu wird der Abstand zwischen Wörtern und Zeichen gestreckt oder verkleinert, sodass alle Zeilen die gleiche Länge haben. Eine andere Möglichkeit, Text auszurichten, besteht darin, das letzte Wort so zu umbrechen, dass ein Teil des Wortes in der nächsten Zeile erscheint. LATEX (Aus technischer Sicht erledigt das TEX-Texteingabesystem fast die gesamte Arbeit; LATEX baut auf TEX auf. Hier verwende ich aus Gründen der Einfachheit LATEX) versucht, optimale Zeilenumbruchpunkte zu finden, damit der Text schön aussieht. Wenn dies fehlschlägt, enden mehrere Zeilen in einer Zeile mit einem Bindestrich, oder der Abstand zwischen Wörtern in verschiedenen Zeilen unterscheidet sich.LATEX verfügt über eine Reihe von Regeln zur Bewertung des Ausrichtungsfehlers. Das Programm versucht, die Option "am wenigsten schlecht" zu finden.
Wenn ein Absatz n mögliche Zeilenumbruchpunkte hat, gibt es
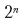mögliche Optionen zum Umbrechen des Textes. Der „Fehler“ der Auswahl für jeden Unterbrechungspunkt hängt davon ab, welche Unterbrechungspunkte zuvor ausgewählt wurden. Daher haben wir wieder überlappende Unteraufgaben. Die Verwendung dynamischer Programmiertechniken reduziert die Ausführungszeit, auf 
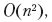die mit zusätzlichen Methoden verbessert werden kann.
»Weitere Details zum Buch finden Sie auf der Website des Verlags.
» Inhaltsverzeichnis
» Auszug
für Einwohner 25% Rabatt auf den Gutschein - Informatik
Nach Bezahlung der Papierversion des Buches wird ein E-Book per E-Mail verschickt.