Was ist die Zukunft der Mathematik?
- In den 1990er Jahren begannen Computer besser Schach zu spielen als Menschen.
- Im Jahr 2018 können Computer Go besser spielen als Menschen.
- Im Jahr 2019 sagte mir der Forscher für künstliche Intelligenz, Christian Szegedy , dass Computer in 10 Jahren ein besserer Satz sein werden als Menschen.
Natürlich kann er sich irren. Oder vielleicht hat er recht.
Ich glaube an Folgendes: In zehn Jahren werden uns Computer helfen, trostlose Theoreme auf der Ebene der frühen Doktoranden zu beweisen. Welche Bereiche der Mathematik? Kommt darauf an, wer sich in diesem Forschungsbereich engagiert.
Das typische Muster für künstliche Intelligenz lautet: Zuerst ist es sehr dumm, und dann wird es plötzlich schlauer. Die natürliche Frage ist: Wann tritt der Phasenübergang auf und die künstliche Intelligenz wird plötzlich sehr intelligent? Antwort: Niemand weiß das. Klar ist, dass je mehr Menschen in diesen Forschungsbereich involviert sind, desto eher wird dies geschehen.
Was ist ein Beweis?
Wenn Sie einen hervorragenden Studenten, einen Forschungsmathematiker und einen Computer fragen, was ein Beweis ist, wie lautet ihre Antwort? Die Antworten des hervorragenden Schülers und des Computers stimmen überein und lauten wie folgt:
Ein Beweis ist eine logische Folge von Aussagen, die aus den Axiomen des gewählten Systems, den zuvor bewiesenen Inferenzregeln und Theoremen besteht, die letztendlich zum Beweis der Aussage führen.Natürlich wäre die Antwort eines Forschungsmathematikers nicht so idealistisch. Für einen Mathematiker ist die Definition von Beweis das, was andere erfahrene Mathematiker als Beweis betrachten. Oder was zur Veröffentlichung in den Annals of Mathematics oder Inventiones angenommen wird.
Hierbei gibt es jedoch ein kleines Problem. Die folgenden Screenshots stammen von der Website der Annals of Mathematics , einer der renommiertesten mathematischen Zeitschriften der Welt.
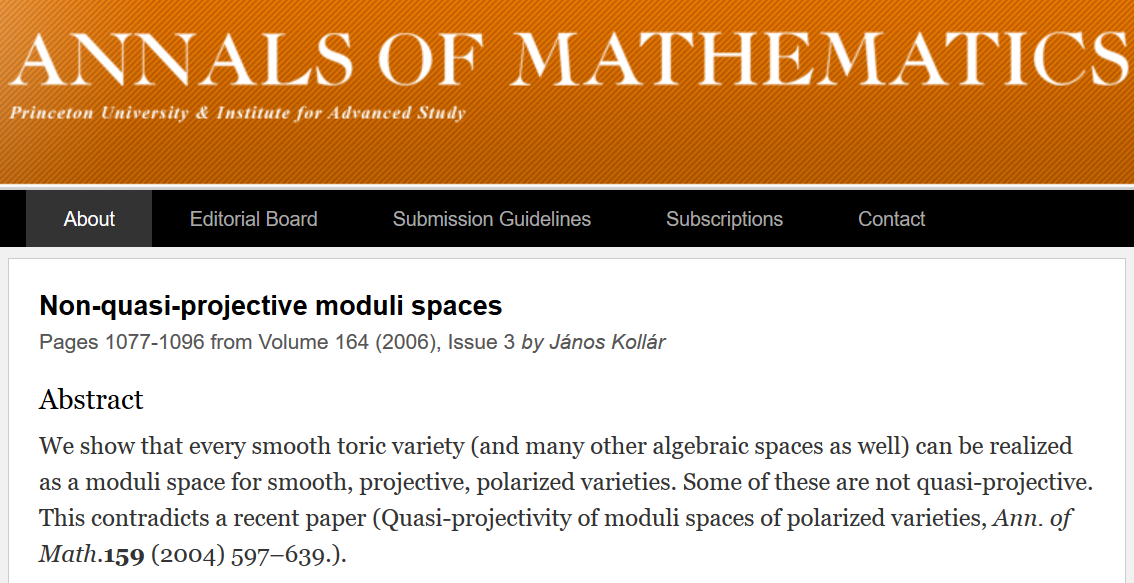
Der zweite Artikel widerspricht buchstäblich dem ersten. Die Autoren schreiben offen darüber in der Anmerkung. Soweit ich weiß, haben die Annals of Mathematics zu keinem dieser Werke eine Gegenargumentation veröffentlicht. Welche Arbeit wird von erfahrenen Mathematikern als richtig angesehen? Sie können dies nur herausfinden, wenn Sie in diesem Bereich arbeiten.
Ausgabe: In der modernen Mathematik ändert sich die Meinung darüber, ob etwas ein Beweis ist, im Laufe der Zeit (zum Beispiel kann es von „ist“ zu „ist nicht“ gehen).
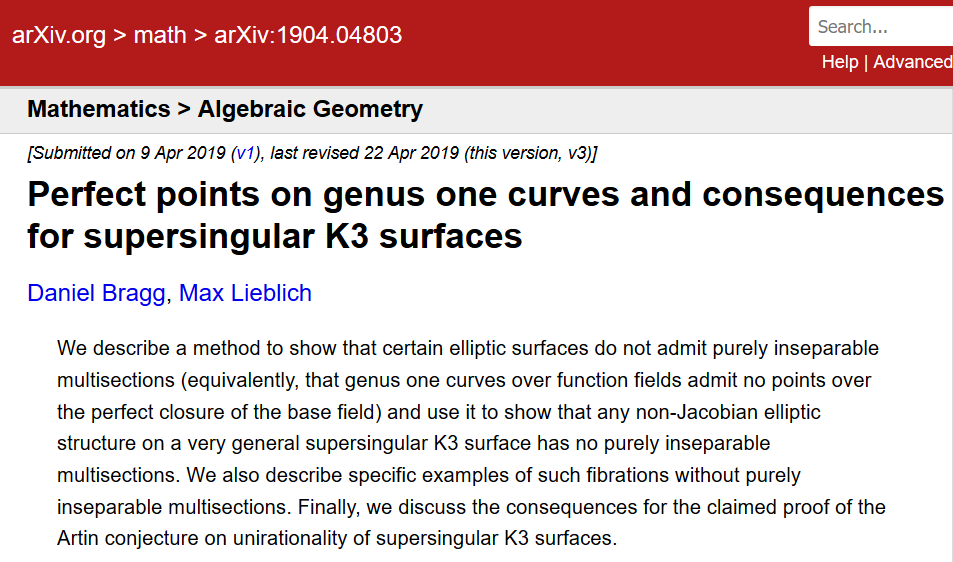
Dieser kurze Artikel aus dem Jahr 2019 zeigt, dass ein weiterer wichtiger Artikel aus dem Jahr 2015, der in Inventiones veröffentlicht wurde, stark von einem falschen Lemma abhängt. Dies wurde erst 2019 bemerkt, obwohl 2016 Workshops abgehalten wurden, um diese wichtige Arbeit zu studieren.
Vladimir Voevodsky, ein Preisträger des Fields-Preises, der zu den Grundlagen der Mathematik beigetragen hat, schreibt: „Wenn ein Autor, dem Menschen vertrauen, ein technisch komplexes Argument schreibt, das schwer zu überprüfen ist, das aber anderen korrekten Argumenten ähnelt, wird dieses Argument kaum jemals auftreten alles wird überhaupt im Detail überprüft. "
Inventiones hat nie eine Widerlegung des Papiers von 2015 veröffentlicht.
Fazit : Die wichtige Mathematik, die veröffentlicht wurde, stellt sich manchmal als falsch heraus. Darüber hinaus werden wir in Zukunft sicherlich mehr Widerlegungen der veröffentlichten Beweise sehen.
Vielleicht basiert meine Arbeit im p-adic Langlands-Programm auf falschen Ergebnissen. Oder optimistischer die richtigen Ergebnisse, die jedoch keinen vollständigen Beweis haben.
Wenn unsere Forschung nicht reproduzierbar ist, können wir sie Wissenschaft nennen? Ich bin mir zu 99,9% sicher, dass Langlands 'p-adic-Programm von der Menschheit niemals dazu verwendet wird, etwas Nützliches zu tun. Wenn meine Arbeit in Mathematik nicht hilfreich ist und garantiert zu 100 Prozent korrekt ist, ist es nur Zeitverschwendung.... Also beschloss ich, die Forschung einzustellen und mich darauf zu konzentrieren, „berühmte“ Mathematik am Computer zu testen.
Im Jahr 2019 fanden Balakrishnan, Dogra, Mueller, Tuitman und Vonk alle rationalen Lösungen für eine bestimmte Gleichung vierten Grades in zwei Variablen. Ausdrücklich:
Diese Berechnung hat eine wichtige Anwendung in der Arithmetik. Der Beweis beruht stark auf der Berechnung in Magma (einem Closed-Source-System) unter Verwendung schneller, nicht referenzierter Algorithmen. Es wäre schwierig, alle Computer auf ein Open-Source-System wie Salbei zu portieren. Dies hat jedoch niemand vor.
Somit bleiben einige der Beweise verborgen. Und vielleicht bleibt es für immer verborgen. Ist das Wissenschaft?
Lücken in Mathe
- 1993 . .
- 1994 , .
- 1995 , , . , , , . , , , .
Was sollte ein Prüfer tun, der einen mathematischen Artikel zur Prüfung erhält? Es wird argumentiert, dass es die Aufgabe des Prüfers ist, „sicherzustellen, dass die im Papier verwendeten Methoden stark genug sind, um das Hauptergebnis des Papiers zu beweisen“.
Was ist, wenn die Methoden stark sind, die Autoren jedoch nicht? So entstehen Situationen, in denen unsere Beweise unvollständig sind. So entsteht die Debatte darüber, ob unsere Theoreme tatsächlich bewiesen sind. So unterrichten wir unsere Schüler überhaupt nicht über Mathematik.
Experten wissen natürlich, welcher Literatur vertraut werden kann und welcher nicht. Aber muss ich ein Experte sein, um zu wissen, welcher Literatur ich vertrauen kann?
Große Lücken in der Mathematik
Anlage A.
Klassifikation einfacher endlicher Gruppen . Experten behaupten, dass wir eine vollständige Klassifizierung einfacher endlicher Gruppen haben. Ich vertraue den Experten.
- 1983 wurde ein fachkundiger Klassifizierungsnachweis angekündigt.
- 1994 fanden Experten einen Fehler (aber lasst uns den Elefanten nicht aus einer Fliege blasen?)
- Im Jahr 2004 wurden mehr als 1000 Seiten veröffentlicht. Der Feldexperte Aschbacher behauptet, der Fehler sei behoben worden, und kündigt einen Plan zur Veröffentlichung von 12 Bänden mit vollständigem Beweis an.
- Im Jahr 2005 wurden nur 6 von 12 Bänden veröffentlicht
- Im Jahr 2010 wurden nur 6 von 12 Bänden veröffentlicht
- Im Jahr 2017 wurden nur 6 von 12 Bänden veröffentlicht
- Im Jahr 2018 wurden der 7. und 8. Band veröffentlicht und ein Hinweis darauf, dass die Veröffentlichung bis 2023 abgeschlossen sein wird.
Von den drei Projektleitern starb einer. Die anderen beiden sind über siebzig.
Anlage B.
Mögliche Modularität abelscher Oberflächen . Vor einem Jahr veröffentlichten mein angesehener Doktorand Toby Gee und drei Mitautoren einen 285-seitigen Vorabdruck mit dem Ergebnis, dass abelsche Oberflächen über vollständig realen Feldern möglicherweise modular sind.
Ihr Beweis zitiert drei unveröffentlichte Preprints (einen im Jahr 2018, einen im Jahr 2015, einen in den 1990er Jahren), ein Internet-Memo aus dem Jahr 2007, eine unveröffentlichte Dissertation in deutscher Sprache und ein Papier, dessen Hauptanspruch später widerlegt wurde. Außerdem sehen wir auf Seite 13 den folgenden Text:
, Arthur’s multiplicity formula GSp4, [Art04]. , , [GT18], , [Art13] [MW16a, MW16b]. , twisted weighted fundamental lemma, [CL10], . , [A24], [A25], [A26] [A27] [Art13], .Können wir ehrlich sagen, dass dies Wissenschaft ist?
Link [CL10] sieht folgendermaßen aus: Die
Arbeit, die mein Doktorand und meine Co-Autoren benötigen, wurde nie veröffentlicht. Höchstwahrscheinlich ist die Aussage richtig. Vielleicht sogar beweisbar.
Und dies sind die Links, auf die in [Art13] verwiesen wird:
Letztes Jahr habe ich Arthur nach diesen Links gefragt, und er hat mir gesagt, dass noch keine Arbeit fertig ist. Natürlich ist Jim Arthur ein Genie. Er hat zahlreiche renommierte Preise gewonnen. Aber er ist auch 75 Jahre alt.
Anlage C.
Gangart - Rozenblyum . Endlose Kategorien haben in letzter Zeit an Popularität gewonnen. Sie werden mit der Zeit noch wichtiger. Die Arbeit des Fields-Preisträgers Peter Scholze beruht auf endlosen Kategorien.
Jacob Lurie hat über 1000 Seiten geschrieben
-kategorisiert und viele Details in meine Arbeit aufgenommen. Gaitsgory - Rozenblyum wollte ähnliche Ergebnisse für
-Kategorien, aber viele Argumente weggelassen, um Zeit zu sparen. "Die ausgelassenen Beweise werden an anderer Stelle erscheinen."
Ich fragte Gaitsgory, wie viel fehlte. Er antwortete, dass es ungefähr 100 Seiten waren. Ich fragte Lurie, was er davon hält. Er antwortete: "Mathematiker unterscheiden sich stark darin, wie gut sie es verstehen, Details wegzulassen."
Bewegt sich die Mathematik zu schnell? Wenn ich ein „Experte“ bin, sollte ich glauben, dass abelsche Oberflächen über völlig realen Feldern möglicherweise modular sind? Um ehrlich zu sein, kenne ich mich nicht mehr.
Auf einer Konferenz an der Carnegie Mellon University, an der ich letzte Woche war, sagte mir Markus Rabe, dass Google an einem Programm arbeitet, das mathematische Preprints von arxiv.org übersetztin eine Sprache, die für die Computerüberprüfung geeignet ist. Ich habe kürzlich auch Arbeiten gesehen, die sich auf einen Artikel meines Schülers stützen, aber nichts über die fehlenden 100 Seiten in [Art13] erwähnen.
Letzter Fehler
Dies ist ein sehr interessantes Beispiel. Das Originalwerk wurde in J. Funct veröffentlicht. Anal. im Jahr 2013. Es gibt einen großen Fehler in der Arbeit (Ungleichheit in die andere Richtung). Der Fehler wurde von S. Gouezel im Jahr 2017 entdeckt, als Gouezel ein Argument mit einem computergestützten Proof-Checking-Programm (Isabelle) formalisierte.
Ein neues Argument wird von Gouezel und dem Autor des Originalwerks vorgelegt. Neue Arbeiten müssen nicht überprüft werden. Der Computer überprüfte 100 Prozent des neuen Arguments. Die Methoden erwiesen sich als stark genug, um den Satz zu beweisen. Und mit „Beweis“ meine ich die klassische, „reine“ Definition von Beweis - das, was wir unseren Schülern beibringen. Jedes Detail des Beweises steht dem Leser zur Verfügung. Wissenschaft ist reproduzierbar. Dies ist die Mathematik, die wir unseren Schülern beibringen. Das ist Mathematik.
Hier sind andere Beispiele für das, was ich für Mathematik halte:
- Typischer Nachweis des Studenten- oder Masterniveaus
- Typischer 100 Jahre alter Beweis für ein wichtiges Ergebnis, das von Zehntausenden Mathematikern gut dokumentiert und recherchiert wurde
- Formeller Beweis von Gonthier, Asperti, Avigad, Bertot, Cohen, Garillot, Le Roux, Mahboubi, O'Connor, Ould Biha, Pasca, Rideau, Solovyev, Tassi, Théry des Feith-Thompson-Theorems.
- Formeller Nachweis der Urheberschaft durch folgende Mathematiker: Hales, Adams, Bauer, Dat Tat Dang, Harrison, Truong Le Hoang, Kaliszyk, Magron, McLaughlin, Thang Tat Nguyen, Truong Quang Nguyen, Nipkow, Obua, Pleso, Rute, Solovyev, An Hoai Thi Ta , Trung Nam Tran, Diep Thi Trieu, Urban, Ky Khac Vu und Zumkellers Beweis für Keplers Vermutung.
Damit ist der Text der Präsentation abgeschlossen, da Kevin zu seinem Hauptteil übergeht: der formalen Überprüfung mathematischer Beweise in Lean, die von Leo de Moura bei Microsoft Research entwickelt wurde. Beispiele waren leider nicht in den Folien enthalten.
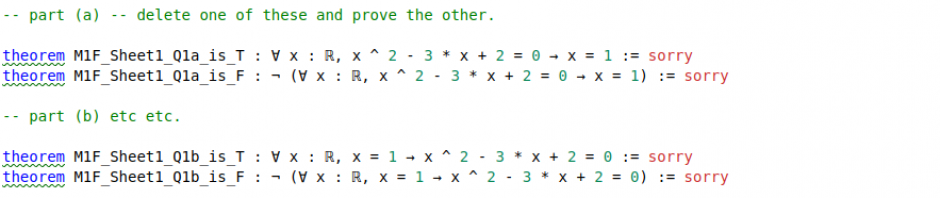
Der Autor ist ein großer Enthusiast für die formale Überprüfung mathematischer Beweise und hat einen sehr interessanten Xena- Blog zu diesem Thema, den ich sehr empfehlen kann.