Korrekturcodes. Der Beginn einer neuen Codierungstheorie

Informationssicherheitsprobleme erfordern das Studium und die Lösung einer Reihe theoretischer und praktischer Probleme bei der Informationsinteraktion von Systemteilnehmern. Unsere Doktrin der Informationssicherheit formuliert die dreigliedrige Aufgabe, die Integrität, Vertraulichkeit und Verfügbarkeit von Informationen sicherzustellen. Die hier vorgestellten Artikel widmen sich der Betrachtung spezifischer Fragen seiner Lösung im Rahmen verschiedener staatlicher Systeme und Teilsysteme. Zuvor hat der Autor in 5 Artikeln die Fragen der Gewährleistung der Vertraulichkeit von Nachrichten anhand staatlicher Standards behandelt. Das allgemeine Konzept des Codierungssystems wurde auch von mir früher gegeben .

Einführung

Durch meine Grundausbildung bin ich kein Mathematiker, aber im Zusammenhang mit den Disziplinen, die ich an der Universität lese, musste ich es akribisch verstehen. Lange und beharrlich las ich die klassischen Lehrbücher unserer führenden Universitäten, eine fünfbändige mathematische Enzyklopädie, viele dünne populäre Broschüren zu bestimmten Themen, aber es gab keine Zufriedenheit. Ein tiefes Leseverständnis trat auch nicht auf.



Alle mathematischen Klassiker konzentrieren sich in der Regel auf den unendlichen theoretischen Fall, und spezielle Disziplinen basieren auf dem Fall endlicher Konstruktionen und mathematischer Strukturen. Der Unterschied in den Ansätzen ist kolossal, das Fehlen oder Fehlen guter vollständiger Beispiele ist möglicherweise der Hauptnachteil und das Fehlen von Lehrbüchern für Universitäten. Es gibt sehr selten ein Problembuch mit Lösungen für Anfänger (für Studienanfänger) und solche, die existieren, sündigen mit Auslassungen in Erklärungen. Im Allgemeinen habe ich mich in gebrauchte technische Buchläden verliebt, dank derer die Bibliothek und bis zu einem gewissen Grad der Wissensspeicher wieder aufgefüllt wurden. Ich hatte die Gelegenheit, viel zu lesen, aber "ging nicht".



Dieser Weg führte mich zu der Frage, was ich alleine tun kann, ohne Buch "Krücken", nur ein leeres Blatt Papier und einen Bleistift mit Radiergummi vor mir zu haben. Es stellte sich heraus, dass es ziemlich viel war und nicht ganz das, was gebraucht wurde. Der schwierige Weg der willkürlichen Selbstbildung wurde beschritten. Die Frage war dies. Kann ich zunächst die Arbeit des Codes erstellen und erklären, der Fehler erkennt und behebt, z. B. Hamming-Code, (7, 4) -Code?



Es ist bekannt, dass der Hamming-Code in vielen Anwendungen auf dem Gebiet der Datenspeicherung und des Datenaustauschs, insbesondere in RAID, weit verbreitet ist. Darüber hinaus befindet es sich im ECC-Speicher und ermöglicht die sofortige Korrektur von Einzel- und Doppelfehlern.

Informationssicherheit. Codes, Chiffren, Steg-Nachrichten

Die Informationsinteraktion durch den Austausch von Nachrichten zwischen den Teilnehmern sollte auf verschiedenen Ebenen und auf verschiedene Weise, sowohl durch Hardware als auch durch Software, geschützt werden. Diese Tools werden im Rahmen bestimmter Theorien (siehe Abbildung A) und Technologien entwickelt, entworfen und erstellt, die in internationalen Abkommen über OSI / ISO-Modelle übernommen wurden.



Der Informationsschutz in Informationstelekommunikationssystemen (ITS) wird praktisch zum Hauptproblem bei der Lösung von Managementproblemen, sowohl auf der Ebene einer einzelnen Person - eines Benutzers - als auch für Unternehmen, Verbände, Abteilungen und den gesamten Staat. Von allen Aspekten des ITKS-Schutzes werden wir in diesem Artikel den Schutz von Informationen während ihrer Extraktion, Verarbeitung, Speicherung und Übertragung in Kommunikationssystemen betrachten.



Um den Themenbereich weiter zu klären, konzentrieren wir uns auf zwei mögliche Richtungen, in denen zwei unterschiedliche Ansätze zum Schutz, zur Darstellung und zur Verwendung von Informationen betrachtet werden: syntaktisch und semantisch. Die Abbildung verwendet Abkürzungen: Codec - Codec - Decoder; shidesh - ein Decoder-Decoder; Kreischen - Concealer - Extraktor.





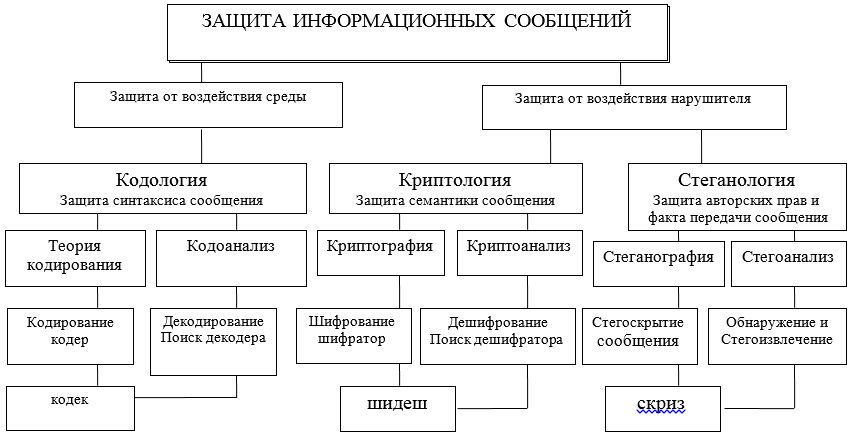
Abbildung A - Diagramm der Hauptrichtungen und Wechselbeziehungen von Theorien zur Lösung der Probleme beim Schutz der Informationsinteraktion



Mit den syntaktischen Merkmalen der Präsentation von Nachrichten können Sie die Richtigkeit und Genauigkeit (fehlerfrei, Integrität) der Präsentation während der Speicherung, Verarbeitung und insbesondere bei der Übertragung von Informationen über Kommunikationskanäle steuern und sicherstellen. Hier werden die Hauptprobleme des Schutzes durch die Methoden der Kodologie gelöst, deren großer Teil - die Theorie der Korrektur von Codes.



Semantische (semantische) SicherheitNachrichten werden durch Methoden der Kryptologie bereitgestellt, die es mittels Kryptographie ermöglichen, einen potenziellen Eindringling vor der Beherrschung des Informationsinhalts zu schützen. In diesem Fall kann der Übertreter die Nachricht und ihren Träger kopieren, stehlen, ändern oder ersetzen oder sogar zerstören, kann jedoch keine Informationen über den Inhalt und die Bedeutung der übertragenen Nachricht erhalten. Der Inhalt der Informationen in der Nachricht bleibt für den Täter unzugänglich. Gegenstand weiterer Überlegungen wird daher der syntaktische und semantische Schutz von Informationen in ITCS sein. In diesem Artikel beschränken wir uns darauf, nur den syntaktischen Ansatz in einer einfachen, aber sehr wichtigen Implementierung durch Korrektur des Codes zu berücksichtigen.



Ich werde sofort eine Trennlinie bei der Lösung von Informationssicherheitsproblemen ziehen: die

Theorie der Kodologiezum Schutz von Informationen (Nachrichten) vor Fehlern (Schutz und Analyse der Syntax von Nachrichten) des Kanals und der Umgebung, um Fehler zu erkennen und zu korrigieren;

Die Theorie der Kryptologie soll Informationen vor unbefugtem Zugriff des Eindringlings auf ihre Semantik schützen (Schutz der Semantik, Bedeutung von Nachrichten).

Die Theorie der Steganologie soll den Informationsaustausch von Nachrichten sowie das Urheberrecht und personenbezogene Daten (Schutz des medizinischen Geheimnisses) schützen.



Im Allgemeinen gehen wir. Per Definition, und es gibt einige davon, ist es nicht einmal leicht zu verstehen, dass es Code gibt. Die Autoren schreiben, dass der Code ein Algorithmus, eine Anzeige und etwas anderes ist. Ich werde hier nicht über die Klassifizierung von Codes schreiben, ich werde nur sagen, dass der (7, 4) -Code blockiert ist .



Irgendwann wurde mir klar, dass es sich bei dem Code um spezielle Codewörter handelt, eine endliche Menge davon, die durch spezielle Algorithmen mit dem Originaltext der Nachricht auf der Sendeseite des Kommunikationskanals ersetzt und über den Kanal an den Empfänger gesendet werden. Das Ersetzen wird von der Codiervorrichtung durchgeführt, und auf der Empfangsseite werden diese Wörter von der Decodiervorrichtung erkannt.



Da die Rolle der Parteien veränderbar ist, werden diese beiden Geräte zu einem zusammengefasst und als abgekürzter Codec (Encoder / Decoder) bezeichnet und an beiden Enden des Kanals installiert. Da es Wörter gibt, gibt es auch ein Alphabet. Das Alphabet besteht aus zwei Zeichen {0, 1}, BlockbinärCodes. Das natürliche Sprachalphabet (NL) besteht aus einer Reihe von Symbolen - Buchstaben, die die Laute der mündlichen Sprache beim Schreiben ersetzen. Hier werden wir uns nicht mit Hieroglyphenschrift in Silben- oder Knotenschrift befassen.



Das Alphabet und die Wörter sind bereits eine Sprache, es ist bekannt, dass natürliche menschliche Sprachen redundant sind, aber was dies bedeutet, wo Sprachredundanz schwer zu sagen ist, ist Redundanz nicht sehr gut organisiert, chaotisch. Beim Codieren und Speichern von Informationen verringern sie tendenziell die Redundanz, z. B. Archivierer, Morsecode usw.



Richard Hemming hat wahrscheinlich früher als andere erkannt, dass Redundanz, wenn sie nicht beseitigt, sondern angemessen organisiert ist, in Kommunikationssystemen verwendet werden kann, um Fehler zu erkennen und sie automatisch in den Codewörtern des übertragenen Textes zu korrigieren. Er erkannte, dass alle 128 7-Bit-Binärwörter verwendet werden können, um Fehler in Codewörtern zu erkennen, die einen Code bilden - eine Teilmenge von 16 7-Bit-Binärwörtern. Es war eine brillante Vermutung.



Vor der Erfindung von Hamming wurden Fehler auch von der Empfangsseite erkannt, wenn der decodierte Text nicht gelesen werden konnte oder sich herausstellte, dass nicht ganz das erforderlich war. In diesem Fall wurde eine Anfrage an den Absender der Nachricht gesendet, um die Blöcke bestimmter Wörter zu wiederholen, was natürlich sehr unpraktisch war und die Kommunikationssitzungen verlangsamte. Dies war ein großes Problem, das seit Jahrzehnten nicht mehr gelöst worden war.

Konstruktion eines (7, 4) Hamming-Codes

Gehen wir zurück nach Hamming. Wörter des (7, 4) -Codes werden aus 7 Bits j = gebildet$$ , j = 0 (1) 15, 4-Informations- und 3-Prüfsymbole, d.h. im Wesentlichen redundant, da sie keine Nachrichteninformationen enthalten. Es war möglich, diese drei Prüfziffern durch lineare Funktionen von 4 Informationssymbolen in jedem Wort darzustellen, wodurch sichergestellt wurde, dass ein Fehler und seine Position in Wörtern erkannt wurden, um eine Korrektur vorzunehmen. Ein (7, 4) -Code erhielt ein neues Adjektiv und wurde zu einerlinearen Blockbinärdatei. Lineare funktionale Abhängigkeiten (Regeln (*)) zur Berechnung von Symbolwerten$(i_1,i_2,i_3,i_4,p_1,p_2,p_3)$





$$ sind wie folgt:$p_i$



$$$p_1 + i_2 +i_3 + i_4 = 0, → p_1 = i_2 + i_3 + i_4,$

$$$p_2 + i_1 + i_3 + i_4 = 0, → p_2 = i_1+ i_3 + i_4, (*)$

$$ Das Korrigieren des Fehlers wurde zu einer sehr einfachen Operation - ein Zeichen (Null oder Eins) wurde im fehlerhaften Bit bestimmt und durch ein anderes entgegengesetztes 0 durch 1 oder 1 durch 0 ersetzt. Wie viele verschiedene Wörter bilden den Code? Die Antwort auf diese Frage für den (7, 4) -Code ist sehr einfach. Da es nur 4 Informationsziffern gibt, hat ihre Vielfalt, wenn sie mit Symbolen gefüllt ist$p_3 + i_1 + i_2 + i_4 = 0, → p_3 = i_1+i_2 + i_4.$





$$ = 16 Optionen, dann gibt es einfach keine anderen Möglichkeiten, dh ein Code, der nur aus 16 Wörtern besteht, stellt sicher, dass diese 16 Wörter das gesamte Schreiben der gesamten Sprache darstellen. Die Informationsteile dieser 16 Wörter sind mit # ($2^4$





$$ ): 0 = 0000; 4 = 0100; 8 = 1000; 12 = 1100; 1 = 0001; 5 = 0101; 9 = 1001; 13 = 1101; 2 = 0010; 6 = 0110; 10 = 1010; 14 = 1110; 3 = 0011; 7 = 0111; 11 = 1011; 15 = 1111. Jedes dieser 4-Bit-Wörter muss berechnet und rechts durch 3 Prüfbits hinzugefügt werden, die gemäß den Regeln (*) berechnet werden. Zum Beispiel haben wir für das Informationswort Nr. 6 gleich 0110$i_1,i_2,i_3,i_4$













$$ und Berechnungen von Prüfsymbolen ergeben das folgende Ergebnis für dieses Wort:$i_1=0, i_2=1, i_3=1,i_4=0$



$$$(_1 = 0, _2 = 1, _3 = 1)$

$$$_1=i_2 +i_3 +i_4 =1 + 1 + 0(mod2)=2(mod2)=0,$

$$$_2=i_1 +i_3 +i_4 =0 + 1 + 0(mod2)=1(mod2)=1,$

$$$_3=i_1 +i_2 +i_4 =0 + 1 + 0(mod2)=1(mod2)=1.$



In diesem Fall hat das sechste Codewort die Form: $$$_6=(i_1,i_2,i_3,i_4,p_1,p_2,p_3)=(0110011).$Ebenso müssen die Prüfsymbole für alle 16 Codewörter berechnet werden. Bereiten wir eine 16-zeilige Tabelle K für die Codewörter vor und füllen die Zellen nacheinander aus (ich empfehle dem Leser, dies mit einem Bleistift in der Hand zu tun).



Tabelle K - Codewörter j, j = 0 (1) 15, (7, 4) - Hamming-Codes



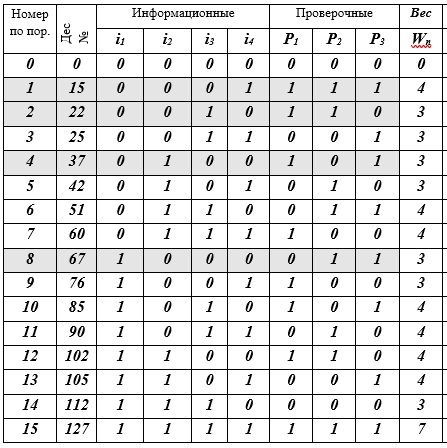
Beschreibung der Tabelle: 16 Zeilen - Codewörter; 10 Spalten: Sequenznummer, Dezimaldarstellung des Codeworts, 4 Informationssymbole, 3 Prüfsymbole, W-Gewicht des Codeworts entspricht der Anzahl der Nicht-Null-Bits (≠ 0). 4 Codewortzeilen werden durch Füllen hervorgehoben - dies ist die Basis des Vektorunterraums. Eigentlich ist das alles - der Code ist aufgebaut.



Somit enthält die Tabelle alle Wörter (7, 4) - den Hamming-Code. Wie Sie sehen, war es nicht sehr schwierig. Als nächstes werden wir darüber sprechen, welche Ideen Hamming zu dieser Codekonstruktion geführt haben. Wir alle kennen den Morsecode, das Marine-Semaphor-Alphabet und andere Systeme, die auf unterschiedlichen heuristischen Prinzipien basieren, aber hier im (7, 4) -Code werden zum ersten Mal strenge mathematische Prinzipien und Methoden verwendet. Die Geschichte wird nur über sie sein.

Mathematische Grundlagen des Codes. Höhere Algebra

Es ist an der Zeit zu erzählen, wie R. Hemming auf die Idee kam, einen solchen Code zu öffnen. Er machte sich keine besonderen Illusionen über sein Talent und formulierte bescheiden eine Aufgabe für sich: einen Code zu erstellen, der einen Fehler in jedem Wort erkennt und korrigiert (tatsächlich wurden sogar zwei Fehler entdeckt, aber nur einer von ihnen wurde korrigiert). Bei Qualitätskanälen ist sogar ein Fehler ein seltenes Ereignis. Daher war Hemmings Plan im Maßstab des Kommunikationssystems immer noch grandios. Nach ihrer Veröffentlichung gab es eine Revolution in der Codierungstheorie.



Es war 1950. Ich gebe hier meine einfache (ich hoffe, verständliche) Beschreibung, die ich von anderen Autoren nicht gesehen habe, aber wie sich herausstellte, ist nicht alles so einfach. Es brauchte Wissen aus zahlreichen Bereichen der Mathematik und Zeit, um alles tief zu verstehen und selbst zu verstehen, warum dies so gemacht wird. Erst danach konnte ich die schöne und ziemlich einfache Idee schätzen, die in diesem Korrekturcode implementiert ist. Die meiste Zeit habe ich mich mit der Technik der Berechnungen und der theoretischen Begründung aller Handlungen beschäftigt, über die ich hier schreibe.



Die Ersteller der Codes konnten sich lange Zeit keinen Code vorstellen, der zwei Fehler erkennt und korrigiert. Die von Hemming verwendeten Ideen haben dort nicht funktioniert. Ich musste schauen und neue Ideen wurden gefunden. Sehr interessant! Fesselt. Es dauerte ungefähr 10 Jahre, um neue Ideen zu finden, und erst danach gab es einen Durchbruch. Codes, die eine beliebige Anzahl von Fehlern anzeigen, wurden relativ schnell empfangen.



Vektorräume, Felder und Gruppen . Der resultierende (7, 4) -Code (Tabelle K) repräsentiert einen Satz von Codewörtern, die Elemente eines Vektorunterraums (der Ordnung 16 mit der Dimension 4) sind, d.h. Teil eines Vektorraums der Dimension 7 mit Ordnung$$$2^7=128.$Von den 128 Wörtern sind nur 16 im Code enthalten, aber sie wurden aus einem bestimmten Grund in den Code aufgenommen.



Erstens sind sie ein Unterraum mit allen folgenden Eigenschaften und Singularitäten, zweitens sind Codewörter eine Untergruppe einer großen Gruppe der Ordnung 128, noch mehr eine additive Untergruppe eines endlichen erweiterten Galois-Feldes GF ($$$2^7$) Ausdehnungsgrad n = 7 und Merkmal 2. Diese große Untergruppe wird durch eine kleinere Untergruppe in benachbarte Klassen zerlegt, was durch die folgende Tabelle D gut veranschaulicht wird. Die Tabelle ist in zwei Teile unterteilt: obere und untere, sollte jedoch als eine lange gelesen werden. Jede benachbarte Klasse (Zeile der Tabelle) ist durch die Äquivalenz der Komponenten ein Element der Faktorgruppe.



Tabelle D - Zersetzung der Additivgruppe des Galois-Feldes GF ($$$2^7$) in Nebenmengen (Zeilen von Tabelle D) für die Untergruppe 16. Ordnung.



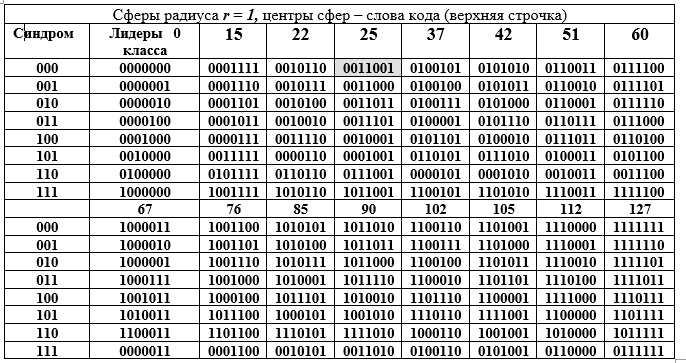
Die Spalten der Tabelle sind Kugeln mit Radius 1. Die linke Spalte (wiederholt) ist das Syndrom des Wortes (7, 4) Hamming-Code, die nächste Spalte ist der Anführer der zusammenhängenden Klasse. Öffnen wir die binäre Darstellung eines der Elemente (das 25. wird durch Füllen hervorgehoben) der Faktorgruppe und ihrer Dezimaldarstellung:



$$$0·x^6+0·x^5+1·x^4+1·x^3+0x^2+0x+1=1·2^4+1·2^3+1·2^0=16+8+1=25$



Technik zum Erhalten von Zeilen der Tabelle D. Ein Element aus der Spalte der Leiter der Klasse wird mit jedem Element aus der Kopfzeile der Spalte der Tabelle D summiert (die Summierung wird für die Zeile des Leiters in binärer Form mod2 durchgeführt). Da alle Klassenleiter das Gewicht W = 1 haben, unterscheiden sich alle Summen von dem Wort in der Spaltenüberschrift nur an einer Position (gleich für die gesamte Zeile, aber unterschiedlich für die Spalte). Tabelle D hat eine wunderbare geometrische Interpretation. Alle 16 Codewörter werden durch die Zentren der Kugeln im 7-dimensionalen Vektorraum dargestellt. Alle Wörter in der Spalte unterscheiden sich vom oberen Wort an derselben Position, dh sie liegen auf der Oberfläche einer Kugel mit dem Radius r = 1.



Diese Interpretation verbirgt die Idee, einen Fehler in einem beliebigen Codewort zu erkennen. Wir arbeiten mit Kugeln. Die erste Bedingung für die Fehlererkennung ist, dass sich Kugeln mit Radius 1 nicht berühren oder schneiden dürfen. Dies bedeutet, dass die Zentren der Kugeln einen Abstand von 3 oder mehr voneinander haben. In diesem Fall schneiden sich die Kugeln nicht nur nicht, sondern berühren sich auch nicht. Dies ist eine Voraussetzung für die Eindeutigkeit der Entscheidung: Welche Sphäre sollte dem fehlerhaften Wort zugeordnet werden, das der Decoder auf der Empfangsseite empfangen hat (kein Code eins von 128 -16 = 112).



Zweitens ist der gesamte Satz von 7-Bit-Binärwörtern mit 128 Wörtern gleichmäßig auf 16 Kugeln verteilt. Der Decoder kann nur ein Wort aus diesem Satz von 128 bekannten Wörtern mit oder ohne Fehler erhalten. Drittens kann die Empfangsseite ein Wort ohne Fehler oder mit Verzerrung empfangen, das jedoch immer zu einer der 16 Kugeln gehört, was vom Decodierer leicht bestimmt werden kann. In der letzteren Situation wird eine Entscheidung getroffen, dass ein Codewort gesendet wurde - der Mittelpunkt einer vom Decodierer bestimmten Kugel, die die Position (Schnittpunkt einer Zeile und einer Spalte) des Wortes in Tabelle D gefunden hat, d. H. Die Spalten- und Zeilennummern.



Hier ergibt sich eine Anforderung für die Wörter des Codes und für den Code als Ganzes: Der Abstand zwischen zwei beliebigen Codewörtern muss mindestens drei betragen, dh die Differenz für ein Paar von Codewörtern, zum Beispiel i = 85 =$$$(i_1,i_2,i_3,i_4,p_1,p_2,p_3)$= 1010101; j = 25 =$$$(i_1,i_2,i_3,i_4,p_1,p_2,p_3)$= 0011001 muss mindestens 3 sein; 85 - 25 = 1010101 - 0011001 = 1001100 = 76, das Gewicht des Differenzworts W (76) = 3. (Tabelle D ersetzt die Berechnung von Differenzen und Summen). Hier wird der Abstand zwischen binären Wortvektoren als die Anzahl nicht übereinstimmender Positionen in zwei Wörtern verstanden. Dies ist die Hamming-Distanz, die in Theorie und Praxis weit verbreitet ist, da sie alle Axiome der Distanz erfüllt.



Bemerkung . Der (7, 4) -Code ist nicht nur ein linearer Block-Binärcode , sondern auch ein Gruppencode, dh die Wörter des Codes bilden durch Addition eine algebraische Gruppe. Dies bedeutet, dass zwei beliebige Codewörter, wenn sie addiert werden, wieder eines der Codewörter ergeben. Nur ist dies keine gewöhnliche Additionsoperation, sondern Additionsmodulo zwei.



Tabelle E - Die Summe der Elemente der Gruppe (Codewörter), die zum Erstellen des Hamming-Codes verwendet wurden



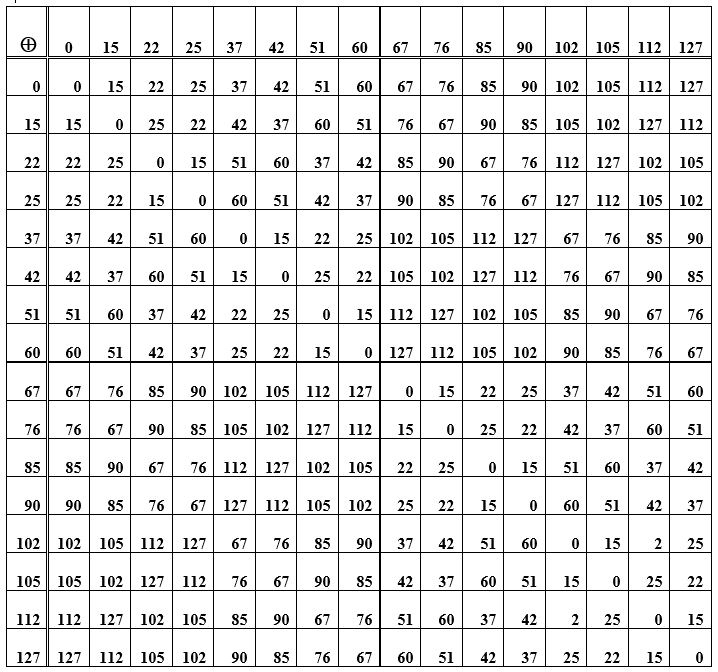
Die Operation zum Summieren von Wörtern selbst ist assoziativ, und für jedes Element in der Menge der Codewörter gibt es ein Gegenteil, dh das Summieren des ursprünglichen Wortes mit dem Gegenteil ergibt den Wert Null. Dieses Null-Codewort ist das neutrale Element in der Gruppe. In Tabelle D ist dies die Hauptdiagonale von Nullen. Der Rest der Zellen (Zeilen- / Spaltenschnittpunkte) sind Zahlen-Dezimal-Darstellungen von Codewörtern, die durch Summieren von Elementen aus einer Zeile und einer Spalte erhalten werden. Wenn Sie die Wörter an bestimmten Stellen neu anordnen (beim Hinzufügen), bleibt das Ergebnis gleich, außerdem haben Subtraktion und Addition von Wörtern das gleiche Ergebnis. Ferner wird ein Codierungs- / Decodierungssystem in Betracht gezogen, das das Syndromprinzip implementiert.

Code-Anwendung. Codierer

Der Encoder befindet sich auf der Sendeseite des Kanals und wird vom Absender der Nachricht verwendet. Der Absender der Nachricht (der Autor) bildet die Nachricht im natürlichen Alphabet und präsentiert sie in digitaler Form. (Der Name des Zeichens im ASCII-Code und in Binärform).

Es ist praktisch, Texte in Dateien für einen PC mit einer Standardtastatur (ASCII-Codes) zu generieren. Jedes Zeichen (Buchstabe des Alphabets) in dieser Codierung entspricht einem Oktett von Bits (acht Bits). Für den (7, 4) - Hamming-Code, in dessen Wörtern nur 4 Informationssymbole vorhanden sind, sind beim Codieren eines Tastatursymbols in einen Buchstaben zwei Codewörter erforderlich, d.h. Ein Oktett eines Buchstabens wird in zwei Informationswörter der natürlichen Sprache (NL) des Formulars aufgeteilt

$$$i<4> = <i_1, i_2, i_3, i_4>$...



Beispiel 1 . Es ist notwendig, das Wort "Ziffer" nach NL zu übertragen. Wir geben die ASCII-Codetabelle ein, die Buchstaben entsprechen: c –11110110 und –11101000, f - 11110100, p - 11110000 und - 11100000 Oktetten. Oder anders gesagt, in ASCII-Codes ist das Wort "Ziffer" = 1111 0110 1110 1000 1111 0100 1111 0000 1110 0000



mit einer Aufteilung in Tetraden (jeweils 4 Ziffern). Somit erfordert die Codierung des Wortes "Ziffer" NL 10 Codewörter des (7, 4) Hamming-Codes. Die Tetraden repräsentieren die Informationsbits der Nachrichtenwörter. Diese Informationswörter (Tetraden) werden in Codewörter (jeweils 7 Bit) umgewandelt, bevor sie an den Kommunikationsnetzwerkkanal gesendet werden. Dies erfolgt durch Vektor-Matrix-Multiplikation: das Informationswort durch die Erzeugungsmatrix. Die Bequemlichkeitszahlung ist sehr teuer und zeitaufwändig, aber alles funktioniert automatisch und vor allem ist die Nachricht vor Fehlern geschützt.

Die Erzeugungsmatrix des (7, 4) Hamming-Codes oder des Codewortgenerators wird erhalten, indem die Basisvektoren des Codes ausgeschrieben und zu einer Matrix kombiniert werden. Dies folgt aus dem Satz der linearen Algebra: Jeder Vektor eines Raums (Unterraums) ist eine lineare Kombination von Basisvektoren, d.h. linear unabhängig in diesem Raum. Dies ist genau das, was erforderlich ist - um Vektoren (7-Bit-Codewörter) aus 4-Bit-Informationsvektoren zu erzeugen.



Die Erzeugungsmatrix des (7, 4, 3) Hamming-Codes oder des Codewortgenerators hat die Form:





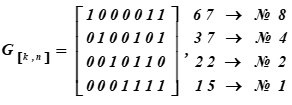
Rechts sind die Dezimaldarstellungen der Codewörter der Basis des Unterraums und ihre Seriennummern in der Tabelle K

Nr. I Zeilen der Matrix sind die Wörter des Codes, die die Basis des Vektorunterraums bilden.



Ein Beispiel zum Codieren der Wörter von Informationsnachrichten (die Erzeugungsmatrix des Codes wird aus den Basisvektoren aufgebaut und entspricht dem Teil der Tabelle K). In der ASCII-Codetabelle nehmen wir den Buchstaben q = <1111 0110>.



Informationswörter der Nachricht sehen aus wie:



$$$i_{k1} = <1111>, i_{k2} = <0110>$...



Dies ist die Hälfte des Zeichens (c). Für den zuvor definierten (7, 4) -Code ist es erforderlich, die Codewörter zu finden, die dem Informationsnachrichtenwort (c) mit 8 Zeichen in der folgenden Form entsprechen:



$$$i_{k1} = <1111>, i_{k2} = <0110>$...



Um diese Buchstabennachricht (q) in Codewörter u umzuwandeln, wird jede Hälfte der Buchstabennachricht i mit der Erzeugungsmatrix G [k, n] des Codes multipliziert (Matrix für Tabelle K):







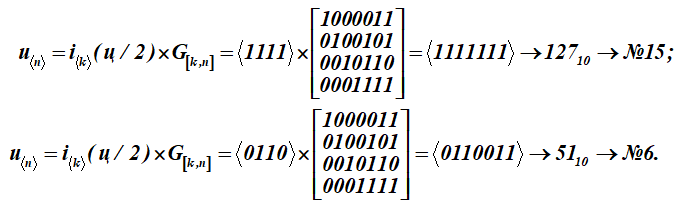
Wir haben zwei Codewörter mit den Seriennummern 15 und 6.



Zeigen detaillierte Bildung des unteren Ergebnisses Nr. 6 - ein Codewort (Multiplikation einer Zeile eines Informationsworts mit den Spalten einer Erzeugungsmatrix); Summation über (mod2)



<0110> ∙ <1000> = 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 0 = 0 (mod2);

<0110> 01 <0100> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 0 = 1 (mod2);

<0110> 00 <0010> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 0 = 1 (mod2);

<0110> ∙ <0001> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 1 = 0 (mod2);

<0110> ∙ <0111> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 1 + 0 ∙ 1 = 0 (mod2);

<0110> 10 <1011>= 0 ≤ 1 + 1 ≤ 0 + 1 ≤ 1 + 0 ≤ 1 = 1 (mod2);

<0110> ∙ <1101> = 0 ∙ 1 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 1 = 1 (mod2).



Als Ergebnis der Multiplikation erhalten das fünfzehnte und sechste Wort aus Tabelle K. Die ersten vier Bits in diesen Codewörtern (Multiplikationsergebnisse) repräsentieren Informationswörter. Sie sehen aus wie:$$$i_{k1} = <1111>, i_{k2}= <0110>$, (in der ASCII-Tabelle ist es nur die Hälfte des Buchstabens t). Für die Codierungsmatrix wird eine Reihe von Wörtern mit den Zahlen 1, 2, 4, 8 als Basisvektoren in Tabelle K ausgewählt. In der Tabelle werden sie durch Füllen hervorgehoben. Dann erhält die Codierungsmatrix für diese Tabelle K die Form G [k, n].



Als Ergebnis der Multiplikation wurden 15 und 6 Wörter der K-Codetabelle erhalten.

Code-Anwendung. Decoder

Der Decoder befindet sich auf der Empfangsseite des Kanals, auf dem sich der Empfänger der Nachricht befindet. Der Zweck des Decoders besteht darin, dem Empfänger die übertragene Nachricht in der Form bereitzustellen, in der sie zum Zeitpunkt des Sendens beim Absender vorhanden war, d. H. Der Empfänger kann den Text verwenden und die Informationen daraus für seine weitere Arbeit verwenden.



Die Hauptaufgabe des Decoders besteht darin, zu prüfen, ob das empfangene Wort (7 Bit) dasjenige ist, das auf der Sendeseite gesendet wurde, ob das Wort Fehler enthält. Um dieses Problem zu lösen, wird für jedes vom Decodierer empfangene Wort durch Multiplizieren mit der Prüfmatrix H [nk, n] ein kurzes Vektorsyndrom S (3 Bits) berechnet.



Für Wörter, die Code sind, dh keine Fehler enthalten, nimmt das Syndrom immer einen Nullwert S = <000> an. Für ein Wort mit einem Fehler ist das Syndrom nicht Null S ≠ 0. Der Wert des Syndroms ermöglicht es, die Position des Fehlers bis zu einem Bit in dem auf der Empfangsseite empfangenen Wort zu erfassen und zu lokalisieren, und der Decodierer kann den Wert dieses Bits ändern. In der Prüfmatrix des Codes findet der Decoder eine Spalte, die dem Wert des Syndroms entspricht, und die Ordnungszahl dieser Spalte entspricht dem durch den Fehler verzerrten Bit. Danach ändert der Decoder für Binärcodes dieses Bit - ersetzen Sie es einfach durch den entgegengesetzten Wert, dh eins wird durch Null ersetzt und Null wird durch Eins ersetzt.



Der betreffende Code ist systematischDas heißt, die Symbole des Informationsworts werden in einer Reihe in den höchstwertigen Bits des Codeworts platziert. Die Wiederherstellung von Informationswörtern erfolgt durch einfaches Verwerfen der niedrigstwertigen (Prüf-) Bits, deren Anzahl bekannt ist. Als nächstes wird eine Tabelle mit ASCII-Codes in umgekehrter Reihenfolge verwendet: Die Eingabe sind Informationsbinärsequenzen und die Ausgabe sind die Buchstaben des Alphabets in natürlicher Sprache. Der (7, 4) -Code ist also systematisch, gruppenweise , linear, blockweise, binär .



Die Basis des Decoders bildet die Prüfmatrix H [nk, n], die die Anzahl der Zeilen gleich der Anzahl der Prüfsymbole und alle möglichen Spalten mit Ausnahme von Null Spalten mit drei Zeichen enthält$$$2^3 – 1 = 7$... Die Paritätsprüfmatrix ist aus den Wörtern der Tabelle K aufgebaut, sie sind so gewählt, dass sie orthogonal zur Codierungsmatrix sind, d.h. ihr Produkt ist die Nullmatrix. Die Prüfmatrix hat bei Multiplikationsoperationen die folgende Form, sie wird transponiert. Für ein spezifisches Beispiel ist die Prüfmatrix H [nk, n] unten angegeben:











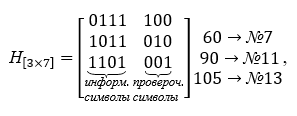
Wir sehen, dass das Produkt aus der Erzeugungsmatrix und der Prüfmatrix eine Nullmatrix ergibt.



Beispiel 2. Dekodieren eines Wortes des Hamming-Codes ohne Fehler (e <7> = <0000000>).

Am Empfangsende des Kanals seien die Wörter # 7 → 60 und # 13 → 105 aus Tabelle K empfangen,

u <7> + e <7> = <0 1 1 1 1 0 0> + <0 0 0 0 0 0>,

Wenn kein Fehler vorliegt, hat er die Form e <7> = <0 0 0 0 0 0 0>.





Infolgedessen hat das berechnete Syndrom einen Nullwert, der das Fehlen eines Fehlers in den Wörtern des Codes bestätigt.



Beispiel 3 . Erkennung eines Fehlers in einem am Empfangsende des Kanals empfangenen Wort (Tabelle K).



A) Angenommen, es ist erforderlich, das 7. Codewort zu übertragen, d.h.



u <7> = <0 1 1 1 1 0 0> und in einem dritten Bit von links wurde ein Fehler gemacht. Dann wird mod2 mit dem 7. Codewort summiert, das über den Kommunikationskanal

u <7> + <7> = <0 1 1 1 1 0 0> + <0 0 1 0 0 0> = <0 1 0 1 übertragen wird 1 0 0>,

wobei der Fehler die Form e <7> = <0 0 1 0 0 0 0> hat.



Das Feststellen der Tatsache der Verzerrung des Codeworts erfolgt durch Multiplizieren des empfangenen verzerrten Wortes mit der Prüfmatrix des Codes. Das Ergebnis dieser Multiplikation ist ein Vektorgenannt Codewort-Syndrom.



Lassen Sie uns eine solche Multiplikation für unsere ursprünglichen Daten (7. Vektor mit einem Fehler) durchführen.





Als Ergebnis einer solchen Multiplikation am Empfangsende des Kanals erhielten wir ein Vektorsyndrom Snk, dessen Dimension (n - k) ist. Wenn das Syndrom S3 = <0,0,0> Null ist, wird geschlossen, dass das auf der Empfangsseite empfangene Wort zum C-Code gehört und ohne Verzerrung übertragen wird. Wenn das Syndrom nicht gleich Null ist, zeigt sein Wert das Vorhandensein eines Fehlers und seinen Platz im Wort an. Das verzerrte Bit entspricht der Nummer der Spaltenposition der Matrix [nk, n], die mit dem Syndrom übereinstimmt. Danach wird das verzerrte Bit korrigiert und das empfangene Wort vom Decodierer weiter verarbeitet. In der Praxis wird für jedes akzeptierte Wort sofort ein Syndrom berechnet, und wenn ein Fehler vorliegt, wird er automatisch beseitigt.



Während der Berechnungen ist das Syndrom S = <110> für beide Wörter gleich. Wir schauen uns die Check-Matrix an und finden darin die Spalte, die zum Syndrom passt. Dies ist die dritte Spalte von links. Daher wurde der Fehler in der dritten Ziffer von links gemacht, was mit den Bedingungen des Beispiels übereinstimmt. Dieses dritte Bit wird auf den entgegengesetzten Wert geändert, und wir haben die vom Decoder empfangenen Wörter an die Codeform zurückgegeben. Der Fehler wurde gefunden und behoben.



Das ist alles, so funktioniert und funktioniert der klassische (7, 4) Hamming-Code.



Zahlreiche Modifikationen und Upgrades dieses Codes werden hier nicht berücksichtigt, da nicht sie wichtig sind, sondern die Ideen und ihre Implementierungen, die die Codierungstheorie radikal verändert haben, und infolgedessen Kommunikationssysteme, Informationsaustausch und automatisierte Steuerungssysteme.

Fazit

Das Papier betrachtet die wichtigsten Bestimmungen und Aufgaben der Informationssicherheit und nennt Theorien zur Lösung dieser Probleme.



Die Aufgabe, die Informationsinteraktion von Subjekten und Objekten vor Umweltfehlern und vor den Handlungen des Eindringlings zu schützen, gehört zur Kodologie.



Der (7, 4) Hamming-Code, der eine neue Richtung in der Codierungstheorie einleitete - die Synthese von Korrekturcodes - wird im Detail betrachtet.



Die Anwendung strenger mathematischer Methoden bei der Codesynthese wird gezeigt.

Beispiele sollen die Effizienz des Codes veranschaulichen.

Literatur

Peterson W., Weldon E. Fehlerkorrekturcodes: Trans. aus dem Englischen. M.: Mir, 1976, 594 p.

Bleihut R. Theorie und Praxis von Fehlerkontrollcodes. Übersetzt aus dem Englischen. M.: Mir, 1986, 576 p.