Vergleich verschiedener Methoden zum Zusammenführen von zwei sortierten Listen

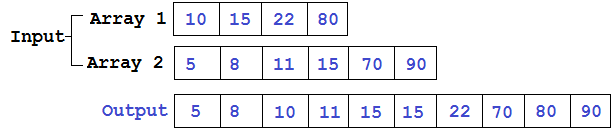
Angenommen, wir haben zwei Listen (der Einfachheit halber Ganzzahlen), die jeweils sortiert sind. Wir wollen sie zu einer Liste zusammenfassen, die ebenfalls sortiert werden muss. Diese Aufgabe ist wahrscheinlich jedem bekannt und wird beispielsweise bei der Zusammenführungssortierung verwendet.

Es gibt viele Möglichkeiten der Implementierung (insbesondere in Python). Schauen wir uns einige davon an und vergleichen Sie die verstrichene Zeit für verschiedene Eingaben.

Die Hauptidee des Algorithmus besteht darin, dass wir durch Platzieren eines Etiketts am Anfang jeder Liste die markierten Elemente vergleichen, das kleinere davon nehmen und das Etikett in seiner Liste zur nächsten Nummer verschieben. Wenn eine der Listen endet, müssen Sie den Rest der zweiten am Ende hinzufügen.

Eingabedaten ändern sich nicht

Es gebe zwei Listen list1und list2.

Beginnen wir mit dem einfachsten Algorithmus beginnen: Lassen Sie uns die Etiketten bezeichnen durch iund jund nehmen Sie die kleineren list1[i], list2[j]und erhöhen das Etikett nach dem anderen , bis eines der Etiketten geht über die Grenze der Liste.

, . , .

:

def simple_merge(list1, list2):
    i, j = 0, 0
    res = []
    while i < len(list1) and j < len(list2):
        if list1[i] < list2[j]:
            res.append(list1[i])
            i += 1
        else:
            res.append(list2[j])
            j += 1
    res += list1[i:]
    res += list2[j:] 
    #   list1[i:]  list2[j:]   ,     
    return res

, . . .

, . , , , , .

def iter_merge(list1, list2):
    result, it1, it2 = [], iter(list1), iter(list2)
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            result.append(el2)
            el2 = next(it2, None)
        else:
            result.append(el1)
            el1 = next(it1, None)
    return result

(result.append()) , . , , .

def gen_merge_inner(it1, it2):
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            yield el2
            el2 = next(it2, None)
        else:
            yield el1
            el1 = next(it1, None)

def gen_merge(list1, list2):
    return list(gen_merge_inner(iter(list1), iter(list2))) #    

python .

• merge heapq. , , , : , , .

  
  
  

  :

  
  
  

  from heapq import merge
  
  def heapq_merge(list1, list2):
  return list(merge(list1, list2)) #   

  
  
  

• Counter collections. Counter , , , , (, ).

  
  
  

  gen_merge_inner Counter(list1) Counter(list2):

  
  
  

  def counter_merge(list1, list2):
  return list(gen_merge_inner(Counter(list1).elements(), Counter(list2).elements()))

  
  
  

• , , . .

  
  
  

  def sort_merge(list1, list2):
  return sorted(list1 + list2)

  
  
  

, ( ). . pop(0) , .

def pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[0] < list2[0] else list2).pop(0))
    return result + list1 + list2

4 , . , , . , . , , .

def reverse_pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[-1] > list2[-1] else list2).pop(-1))
    return (result + list1[-1::-1] + list2[-1::-1])[-1::-1]

.

, :

• simple_merge
• iter_merge
• gen_merge
• heapq_merge
• counter_merge
• sort_merge
• pop_merge
• reverse_pop_merge

timeit. .

: , , , , . .

, $$$1$ $$$10^5$, $$$1$ $$$10^6$.

pop reverse_pop:

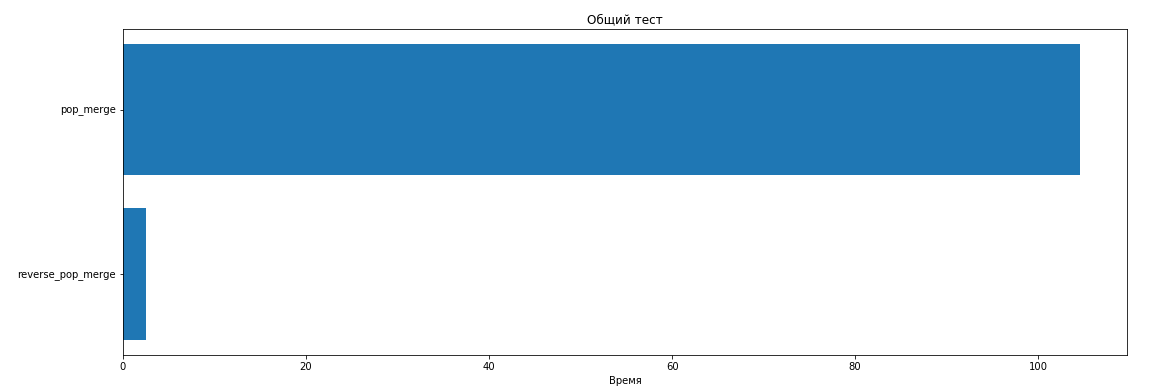
pop_merge , .

pop_merge, :

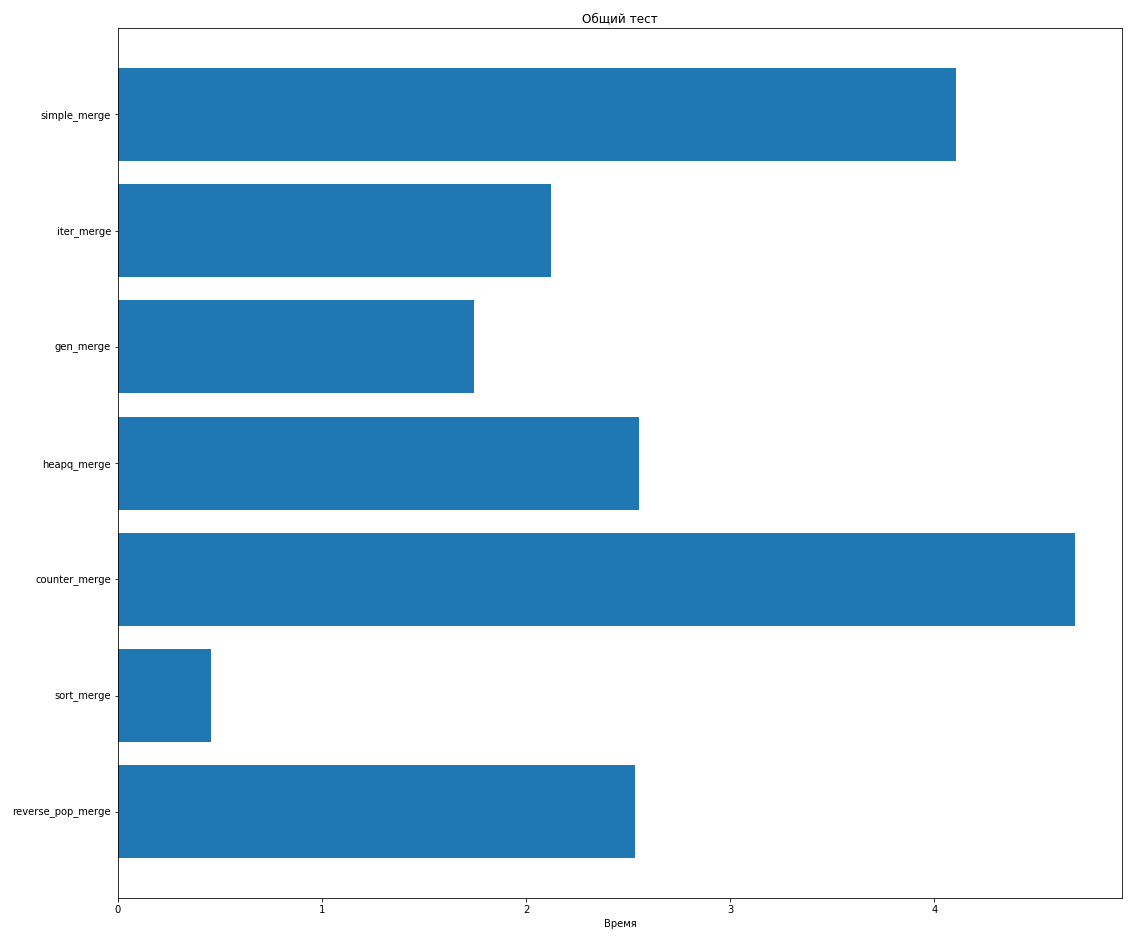
reverse_pop_merge heapq_merge.

, , , .

,

$$$[50x, 50(x+1))$, $$$x$ , $$$1$. $$$50$.

pop_merge heapq_merge, .

, ,

$$$x$, $$$10^4 + 100x$.

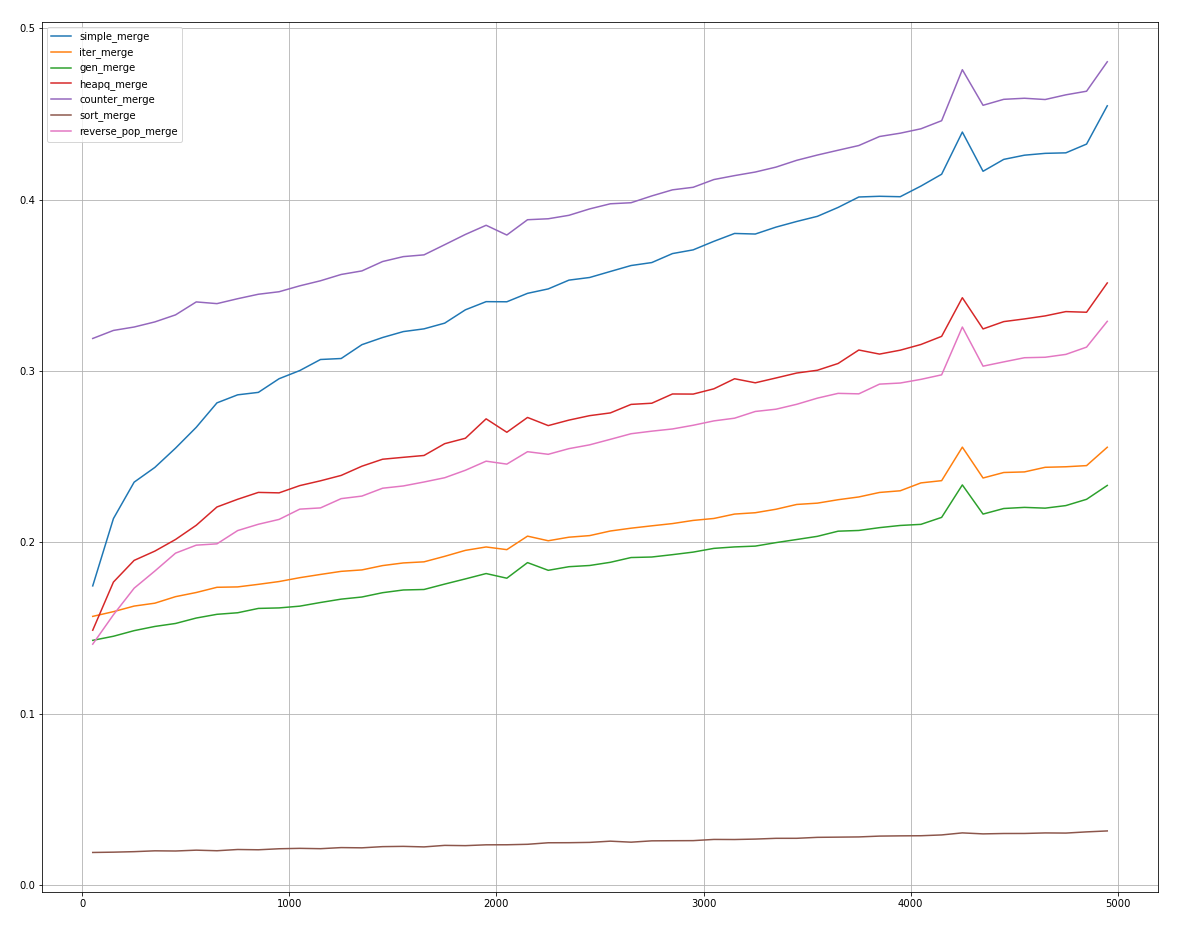
( ) reverse_pop_merge , sort_merge, .

,

, $$$5$, $$$1$.

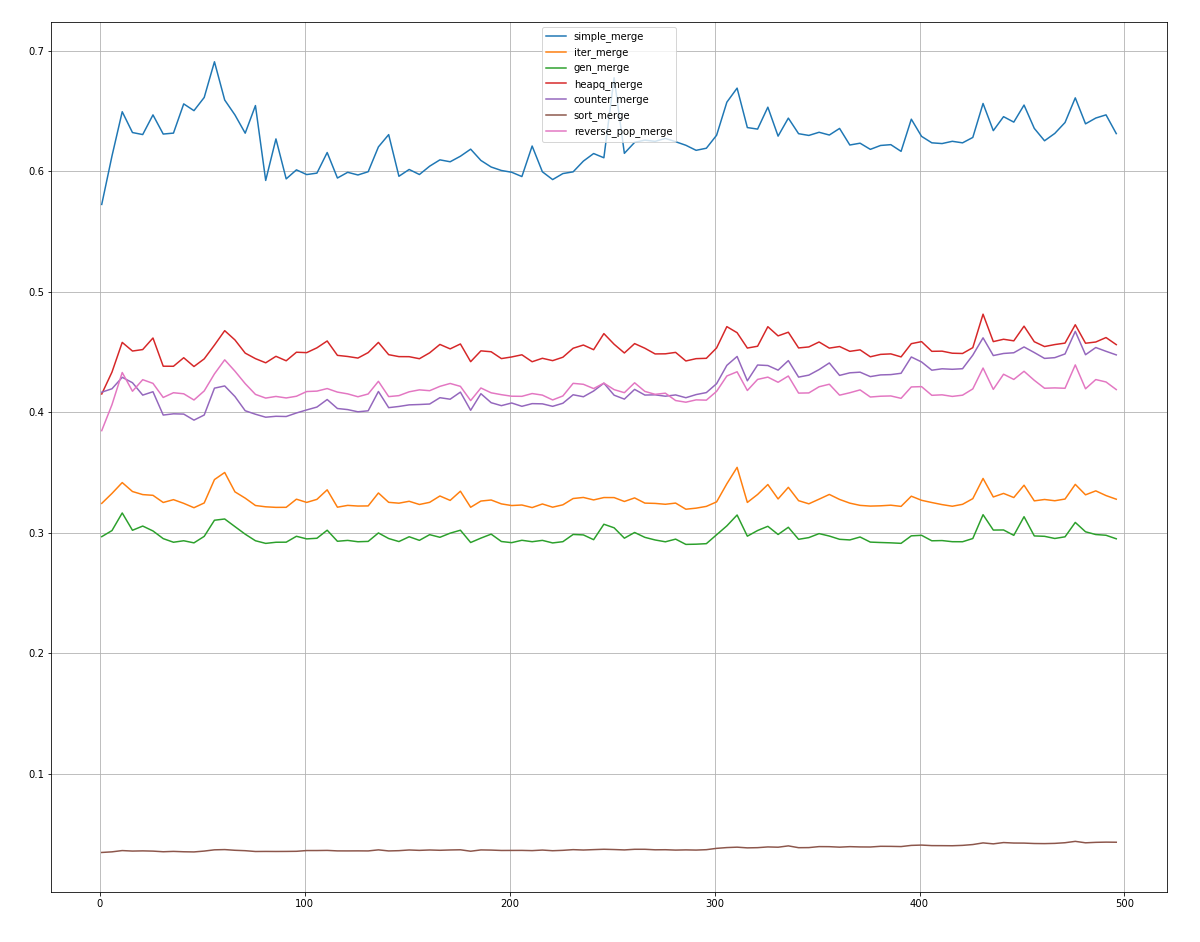
, counter_merge reverse_pop_merge heapq_merge, .

sort_merge! , .

An zweiter Stelle steht in der überwiegenden Mehrheit der Fälle gen_merge, gefolgt von iter_merge.

Die restlichen Methoden verbrauchen noch mehr Zeit, aber einige erzielen in extremen Fällen Ergebnisse von 2-3 Stellen.

PS

Code, Tests, Jupiter-Notizbuch mit Grafiken finden Sie auf gitlab .

Vielleicht ist diese Analyse unvollständig, ich werde gerne Ihre Optionen zum Vergleich hinzufügen, schlagen vor.