Hallo Kollegen! Ich habe seit hundert Jahren nicht mehr über Habr geschrieben, aber jetzt ist es soweit. In diesem Frühjahr unterrichtete ich den Advanced ML-Kurs an der MADE Big Data Academy der Mail.ru Group. Es scheint, dass es den Zuhörern gefallen hat, und jetzt wurde ich gebeten, weniger einen Werbebeitrag als einen Lehrbeitrag zu einem der Themen meines Kurses zu schreiben. Die Wahl lag nahe am Offensichtlichen: Als Beispiel für ein komplexes Wahrscheinlichkeitsmodell diskutierten wir ein äußerst relevantes (scheinbar ... aber dazu später mehr) epidemiologisches SIR-Modell, das die Ausbreitung von Krankheiten in einer Population modelliert. Es hat alles: ungefähre Inferenz durch Markov-Monte-Carlo-Methoden und versteckte Markov-Modelle mit dem stochastischen Viterbi-Algorithmus und sogar reine Anwesenheitsdaten.



Bei diesem Thema kam nur eine kleine Schwierigkeit heraus: Ich fing an, über das zu schreiben, was ich in der Vorlesung tatsächlich erzählte und zeigte ... und irgendwie sammelten sich schnell und unmerklich zwanzig Seiten Text (nun, mit Bildern und Code) an, was immer noch nicht der Fall ist war fertig und war überhaupt nicht in sich geschlossen. Und wenn Sie alles so erzählen, dass es von Grund auf verständlich ist (natürlich nicht vom absoluten Nullpunkt), dann könnten Sie hundert Seiten schreiben. Also werde ich sie eines Tages definitiv schreiben, aber jetzt präsentiere ich Ihnen den ersten Teil der Beschreibung des SIR-Modells, in dem wir nur ein Problem aufwerfen und das Modell von seiner generierenden Seite aus beschreiben können - und wenn die angesehene Öffentlichkeit ein Interesse hat, dann wird es möglich sein Vorgehen.

SIR-Modell: Problemstellung

Ich liebe meine Freunde und sie lieben mich.

Wir sind so nah wie möglich.

Und nur weil es uns wirklich wichtig ist,

was auch immer wir bekommen, wir teilen es!



Tom Lehrer. Ich habe es von Agnes bekommen

Also lasst es uns herausfinden. Informell sind die Grundannahmen des SIR-Modells wie folgt:

• Es gibt eine bestimmte Population von Menschen, in denen ein schreckliches Virus laufen kann.
• Zunächst dringt das Virus auf die eine oder andere Weise in die Bevölkerung ein (zum Beispiel erscheint die erste kranke Person), und dann infizieren sich die Menschen voneinander.
• SIR , :
  
     ○ Susceptible ( , , .. ),
  
     ○ Infected ( )
  
     ○ Recovered ().

Der Einfachheit halber nehmen wir an, dass Kranke immer Immunität entwickeln und in der Natur vom Kreislauf des Virus ausgeschlossen sind. Dementsprechend können Übergänge zwischen diesen Zuständen nur von links nach rechts erfolgen: Anfällig → Infiziert → Wiederhergestellt.



Die Aufgabe besteht in der Tat darin, dieses Modell zu trainieren, dh aus den Daten etwas über die Parameter des Infektionsprozesses zu verstehen. Es ist leicht zu verstehen, wie die Daten aussehen - es ist einfach die Anzahl der registrierten Infizierten zu jedem Zeitpunkt, die wir durch den Vektor bezeichnen werden$$$\boldsymbol{y}$... Als ich zum Beispiel meine Hausaufgaben im Kurs über Coronavirus machte (es handelte sich jedoch um andere Modelle), sahen die Daten für Russland folgendermaßen aus:

[2,2,2,2,3,4,6,8,10,10,10,10,15,20,25,30,45,59,63,93,114,147,199,253,306,438,438,495,658,840,1036,1264,1534,1836,2337,2777,3548,4149,4731,5389,6343,7497,8672]

Was die Parameter dieses Modells sind, wie sie miteinander interagieren und wie sie trainiert werden, insbesondere an einem so kleinen Datensatz, ist eine ernstere Frage.



Im Allgemeinen werde ich dem allgemeinen Umriss der Arbeit folgen ( Fintzi et al., 2016 ), in der MCMC-Algorithmen für SIR, SEIR und einige ihrer Varianten erstellt werden. Im Vergleich zu ( Fintzi et al., 2016 ) werde ich jedoch sowohl das Modell als auch seine Darstellung erheblich vereinfachen. Die Hauptvereinfachung besteht darin, dass wir anstelle der kontinuierlichen Zeit, die in der ursprünglichen Arbeit berücksichtigt wird, die diskrete Zeit betrachten, dh anstelle eines kontinuierlichen Prozesses, der irgendwann Ereignisse der Form "infiziert" und "wiederhergestellt" erzeugt, betrachten wir dass Menschen eine Reihe von diskreten Zeitpunkten durchlaufen$$$t=1,\ldots,T$... Diese Vereinfachung wird es uns erstens ermöglichen, viele technische Schwierigkeiten zu beseitigen und zweitens vom Metropolis-Hastings-Algorithmus im Allgemeinen zum Gibbs- Abtastalgorithmus überzugehen, dh nicht das Metropolis-Verhältnis zu berechnen, wie es in ( Fintzi et al al., 2016 ). Wenn Sie nicht verstehen, was ich gerade gesagt habe, machen Sie sich keine Sorgen: Wir werden dies heute nicht brauchen, und wenn es die nächsten Teile gibt, werde ich dort alles erklären.



Wir werden die Zustände des SIR-Modells mit S, I bzw. R und den Zustand einer Person bezeichnen$$$i$ in dem Augenblick $$$t$ - über $$$x_i^{(t)}\in\{S, I, R\}$... Gleichzeitig werden wir sofort Variablen für die Gesamtzahl der noch nicht erkrankten Patienten einführen.$$$S^{(t)}$krank $$$I^{(t)}$ und erholt $$$R^{(t)}$ in dem Augenblick $$$t$... Total Mann werden wir haben$$$N$also für jeden $$$t$ wird durchgeführt $$$S^{(t)} + I^{(t)} + R^{(t)} = N$... Und wie ich oben schrieb,$$$y^{(t)}$von ihnen sind registrierte (getestete) kranke Menschen.



Die unbekannten Parameter des Modells sind$$$\boldsymbol\theta = \{\beta, \mu, \rho, \boldsymbol{\pi}\}$wo:

• $$$\boldsymbol\pi$ - die anfängliche Verteilung der Fälle; mit anderen Worten,$$$x^{(1)}_j\sim \boldsymbol{\pi}$ für jeden $$$j$;; In unserem vereinfachten Modell werden wir nicht trainieren$$$\boldsymbol\pi$, aber wir werden einfach 1-2 Fälle im ersten Moment der Zeit aufzeichnen;
• $$$\rho$ - die Wahrscheinlichkeit, eine infizierte Person in der Allgemeinbevölkerung zu finden, dh die Wahrscheinlichkeit, dass eine Person gefunden wird $$$x_j$ In dem Moment $$$t$wann $$$x_j^{(t)}=I$wird durch Testen erkannt und in die Daten eingetragen $$$y^{(t)}$;; Mit anderen Worten, wir werfen für jede kranke Person eine Münze, um festzustellen, ob die Prüfung sie findet oder nicht, also ist der aktuelle Gegenstand$$$y_t$ hat eine Binomialverteilung mit Parametern $$$I^{(t)}$ und $$$\rho$::

  $$

  $$y^{(t)}\mid I^{(t)}, \rho \sim \mathrm{Binomial}(I^{(t)}, \rho);$$

• $$$\mu$ - die Wahrscheinlichkeit, dass sich die kranke Person in einem Zeitschritt erholt, dh die Wahrscheinlichkeit eines Übergangs vom Staat $$$I$ im Zustand $$$R$;;

UND $$$\beta$ - Dies ist der interessanteste Parameter, der die Infektionswahrscheinlichkeit einer infizierten Person in einer Zeitspanne anzeigt . Dies bedeutet, dass wir im Modell davon ausgehen, dass alle Menschen in der Bevölkerung miteinander „kommunizieren“ („Kommunikation“ bedeutet hier Kontakt, der für die Übertragung der Krankheit ausreicht; Coronavirus wird hauptsächlich durch Tröpfchen in der Luft übertragen, aber es ist natürlich möglich, und zu modellieren Die Ausbreitung einer anderen Krankheit (siehe z. B. das Epigraph) und die Wahrscheinlichkeit einer Infektion hängen davon ab, wie viele jetzt infiziert sind, dh davon, was ist$$$I^{(t)}$... Wir nehmen das einfachste Modell an, bei dem die Wahrscheinlichkeit einer Infektion durch eine infizierte Person besteht$$$\beta$und all diese Ereignisse sind unabhängig, was bedeutet, dass die Wahrscheinlichkeit, gesund zu bleiben, gleich ist

$$

$$(1-\beta)^{I^{(t)}}.$$

Diese Annahmen haben tatsächlich viel zu diskutieren. Das Überraschendste hier ist meiner persönlichen Meinung nach die Binomialverteilung für$$$y^{(t)}$... Das Werfen einer Münze mit der Wahrscheinlichkeit, eine infizierte Person zu entdecken, ist absolut normal, aber es ist nicht sehr realistisch, dass wir diese Münze bei jedem Schritt erneut werfen, dh wir können eine bereits erkannte infizierte Person „vergessen“. Infolgedessen kann (und tut dies häufig) das SIR-Modell eine vollständig nicht monotone Sequenz erzeugen$$$\boldsymbol{y}$;; Das ist seltsam, aber es scheint keinen großen Einfluss auf das Ergebnis zu haben, und es wäre viel schwieriger, diesen Prozess realistischer zu modellieren.



Darüber hinaus ist es offensichtlich, dass dieses Modell für eine geschlossene Bevölkerung gedacht ist, in der jeder mit jedem "kommuniziert". Daher ist es nicht sinnvoll, es beispielsweise für Russland mit dem Parameter N von einhundert Millionen oder für Moskau mit dem Parameter zehn Millionen (und) zu starten rechnerisch wird nicht funktionieren). Eine wichtige Richtung für Erweiterungen und Erweiterungen von SIR-Modellen ist diesem Thema gewidmet: Wie kann ein realistischeres Diagramm von Interaktionen und möglichen Infektionen hinzugefügt werden? Wir werden wahrscheinlich im letzten, letzten Beitrag darüber sprechen.



Mit all diesen Vereinfachungen können wir nun unter Verwendung der obigen Parameter die Wahrscheinlichkeitsmatrix des Übergangs zwischen Zuständen aufschreiben. Diese Wahrscheinlichkeiten (genauer gesagt die Wahrscheinlichkeit einer Infektion) hängen von der allgemeinen Statistik der Bevölkerung ab. Bezeichnen wir den Vektor der Zustände aller Menschen außer$$$x_j$, über $$$\boldsymbol{x}_{-j}$und erweitern Sie die gleiche Notation auf alle anderen Variablen; z.B,$$$I_{-j}^{(t)}$ Ist die Anzahl der gleichzeitig infizierten Personen $$$t$, ganz zu schweigen von $$$x_j$... Dann für die Wahrscheinlichkeiten des Übergangs von$$$x_j^{(t-1)}$ beim $$$x_j^{(t)}$ wir bekommen

$$

$$p\left(x_j^{(t)}=S\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=R\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = \mu,$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - \mu,$$

und in allen anderen Fällen

$$

$$p\left(x_j^{(t)}\mid x_j^{(t-1)}, \boldsymbol{x}_{-j}^{(t-1)}\right) = 0.$$

Dasselbe kann deutlicher in Form einer Übergangswahrscheinlichkeitsmatrix geschrieben werden (die Reihenfolge der Zeilen und Spalten ist natürlich, SIR):

$$

$$\left(\begin{matrix} (1 - \beta)^{I_{-j}^{(t-1)}} & 1 - (1 - \beta)^{I_{-j}^{(t-1)}} & 0 \\ 0 & 1 - \mu & \mu \\ 0 & 0 & 1\end{matrix}\right)$$

Für einen Leser, der mit Markov-Ketten und Markov-Modellen vertraut ist, scheint es, dass dies nur ein verstecktes Markov-Modell ist: Es gibt einen verborgenen Zustand, es gibt eine klare Verteilung der Observablen für jeden verborgenen Zustand, die Übergänge sind wirklich Markov, das heißt, der nächste verborgene Zustand hängt nur vom vorherigen ab ... Aber es gibt Wie sie sagen, gibt es eine Einschränkung: Die Übergangswahrscheinlichkeiten können nicht als konstant angesehen werden, sie ändern sich mit der Änderung$$$I^{(t)}$und dies ist ein äußerst wichtiger Aspekt des Modells, der nicht weggeworfen werden kann.



Daher wird die Schlussfolgerung in diesem Modell plötzlich viel schwieriger als in dem üblichen versteckten Markov-Modell (obwohl es auch nicht immer ein solches Geschenk gibt). Obwohl die Schlussfolgerung komplizierter ist, unterliegt sie immer noch dem menschlichen Verstand - in den nächsten Installationen (falls vorhanden) werde ich Ihnen darüber erzählen. Und für heute ist fast genug genug - jetzt entspannen wir uns ein wenig und versuchen, vorerst generativ mit diesem Modell zu spielen.

Beispiel für die Datengenerierung

Als großer Kenner und Experte ging ein

Introvertierter in Quarantäne.

***

"Ich konnte zu Hause nicht arbeiten",

versuchte die Biene den Würmern zu erklären.

***

Kaganov starb fröhlich im Scherz.

Natürlich tut er mir sehr leid ...



Leonid Kaganov. Quarantänen

Wenn die Parameter des Modells bekannt sind und Sie nur einen Verlauf der Entwicklung der Krankheit in der Bevölkerung erstellen müssen, ist SIR nicht kompliziert. Der folgende Code generiert ein Beispiel für eine Population gemäß unserem Modell. Staaten, die ich als codiert habe$$$S=0$, $$$I=1$, $$$R=2$... Wie ich gewarnt habe, gehe ich der Einfachheit halber davon aus, dass dies im Moment der Fall ist$$$t=0$ Es gibt genau eine kranke Person in der Bevölkerung, und dann geht es weiter.

def sample_population(N, T, true_rho, true_beta, true_mu):
    true_log1mbeta = np.log(1 - true_beta)

    cur_states = np.zeros(N)
    cur_states[:1] = 1
    cur_I, test_y, true_statistics = 1, [1], [[N-1, 1, 0]]

    for t in range(T):
        logprob_stay_healthy = cur_I * true_log1mbeta
        for i in range(N):
            if cur_states[i] == 0 and np.random.rand() < -np.expm1(logprob_stay_healthy):
                cur_states[i] = 1
            elif cur_states[i] == 1 and np.random.rand() < true_mu:
                cur_states[i] = 2

        cur_I = np.sum(cur_states == 1)
        test_y.append( np.random.binomial( cur_I, true_rho ) )
        true_statistics.append([np.sum(cur_states == 0), np.sum(cur_states == 1), np.sum(cur_states == 2)])

    return test_y, np.array(true_statistics).T

N, T, true_rho, true_beta, true_mu = 100, 20, 0.1, 0.05, 0.1
test_y, true_statistics = sample_population(N, T, true_rho, true_beta, true_mu)

Dieser Code gibt nicht nur die tatsächlichen Daten aus $$$\boldsymbol{y}$aber auch "wahre" Statistiken $$$S^{(t)}$, $$$I^{(t)}$, $$$R^{(t)}$so können sie visualisiert werden. Machen wir das; für Parameter$$$N=100$, $$$T=20$, $$$\rho=0.1$, $$$\beta=0.2$, $$$\mu=0.3$Sie können so etwas bekommen:







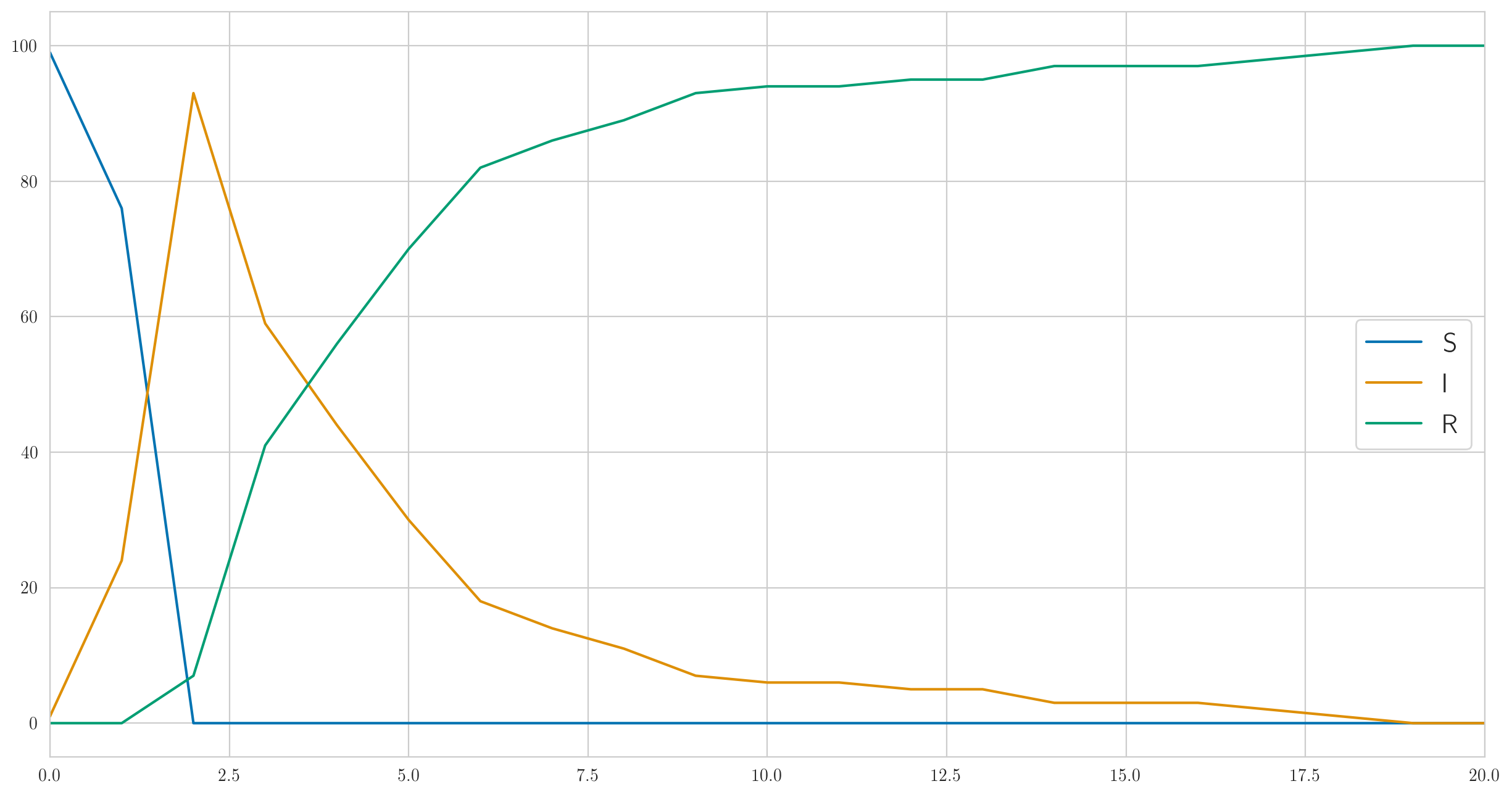
Wie Sie sehen können, werden in diesem Beispiel alle sehr schnell krank und dann langsam langsam besser. Und die tatsächlich beobachteten Daten über die Kranken sehen folgendermaßen aus:

[1 6 13 6 6 4 1 0 0 1 0 1 2 0 0 0 0 0 1 0 0]

Beachten Sie, dass es hier, wie oben erläutert, keine Monotonie gibt.



Dies ist aber sicherlich nicht das einzig mögliche Verhalten. Ich habe die obigen Parameter so gewählt, dass die Infektion schnell genug war und die Krankheit fast sofort alle hundert Personen in unserer Testpopulation abdeckte. Und wenn du es tust$$$\beta$ kleiner zum Beispiel $$$\beta=0.01$Dann wird die Infektion viel langsamer verlaufen und nicht einmal jeder wird Zeit haben, krank zu werden, bevor sich die letzte kranke Person erholt und nicht bleibt. So etwas wie das:







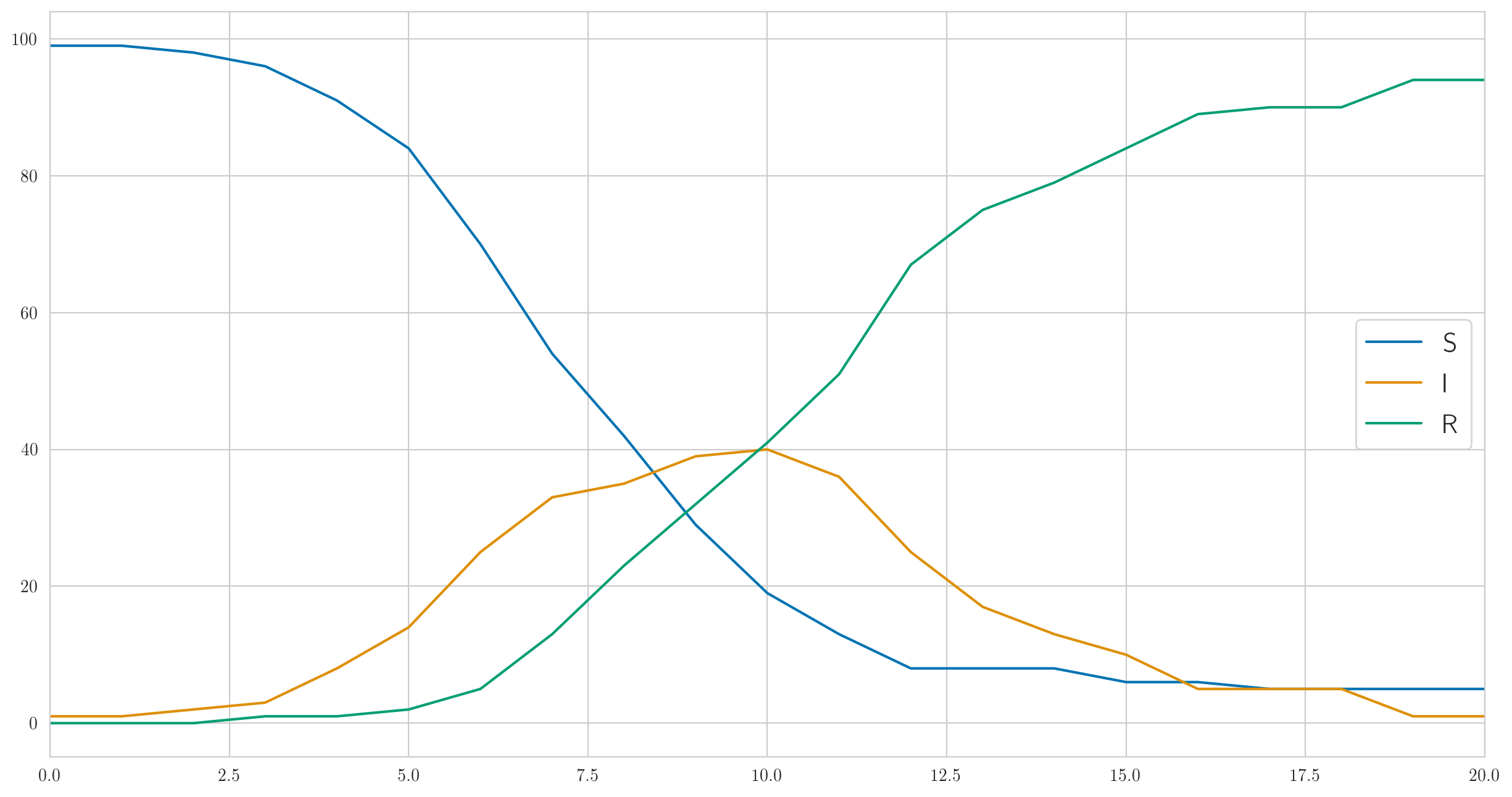
Und die Anzahl der erkannten Fälle ist auch völlig anders:

[1 0 0 0 0 1 2 2 3 1 1 9 3 1 3 1 0 1 0 0 0]

Es ist möglich, die Krankheit noch mehr zu "erwürgen"; Lass uns zum Beispiel gehen$$$\beta=0.01$aber setzen $$$\mu=0.5$Das heißt, in jedem Zeitintervall hat jede kranke Person eine Chance, sich um 0,5 zu erholen (am Ende ist dies logisch: Entweder wird sie sich erholen oder nicht). Dann werden nur 50-60 von 100 Menschen an dem schrecklichen Virus erkranken; Kurven können so aussehen:

[1 0 0 1 3 2 1 1 0 3 0 0 0 0 0 1 0 0 0 0 0]

Aber das Gesamtbild sieht natürlich auf jeden Fall ungefähr gleich aus: zuerst exponentielles Wachstum und dann der Ausgang zur Sättigung; Der einzige Unterschied besteht darin, ob der letzte Netzbetreiber Zeit hat, sich zu erholen, bevor alle neu gestartet werden.



Nun, es ist Zeit, die Zwischenergebnisse zusammenzufassen. Heute haben wir gesehen, wie eines der einfachsten epidemiologischen Modelle aussieht. Trotz vieler stark vereinfachender Annahmen ist das SIR-Modell auch in dieser Form immer noch sehr nützlich. Tatsache ist, dass die meisten seiner Erweiterungen ziemlich einfach sind und das allgemeine Wesen der Sache nicht ändern. Wenn wir fortfahren, werde ich in der nächsten Serie darüber sprechen, wie man ein SIR-Modell trainiert. Dies wird jedoch so viele interessante Dinge mit sich bringen, dass es wahrscheinlich auch nicht in einen Beitrag passt. Bis zum nächsten Mal!