Johnsons Algorithmus auf einem Digraphen mit negativen Bögen

Der Artikel wurde am Vorabend des Kursbeginns "Algorithmen und Datenstrukturen" erstellt.

---

Johnsons Algorithmus findet den kürzesten Weg zwischen allen Eckpunktpaaren in einem gewichteten gerichteten Graphen mit negativen Gewichten ohne negative Konturen.

Oh, wie es sich anhört! Lassen Sie uns die Problemstellung in Teilen analysieren.

, , ( – ), . , 4 8 :

. «» «».

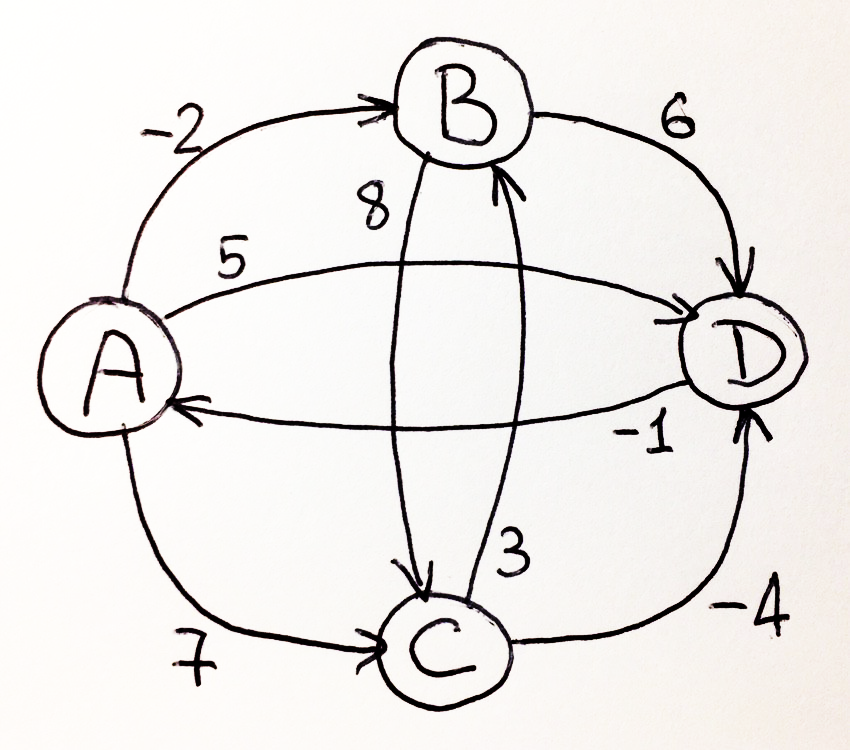
, «» «» . , . – . , D , .

, , , . . . «» «», , , .

, , , :

.

-, « » :

for k = 1 to n // n –    
    for x = 1 to n
        for y = 1 to n
            W[x][y] = min(W[x][y], W[x][k] + W[k][y])

W[x][y] .

W – . , .

«» . X Y , – .

- , – , – .

. , , , -.

, .

, , (-2), «» D (-2+6=4). . CD .

. , .

?

: ! : , , . !

?

– , . ? , .

, 4, A D : 5 + 1 * 4 = 9. 3 (A-B-C-D) 12 : -2 + 8 – 4 + 3 * 4 = 14.

, – , . ? XY h(X) h(Y), h(v) – «» , .

:

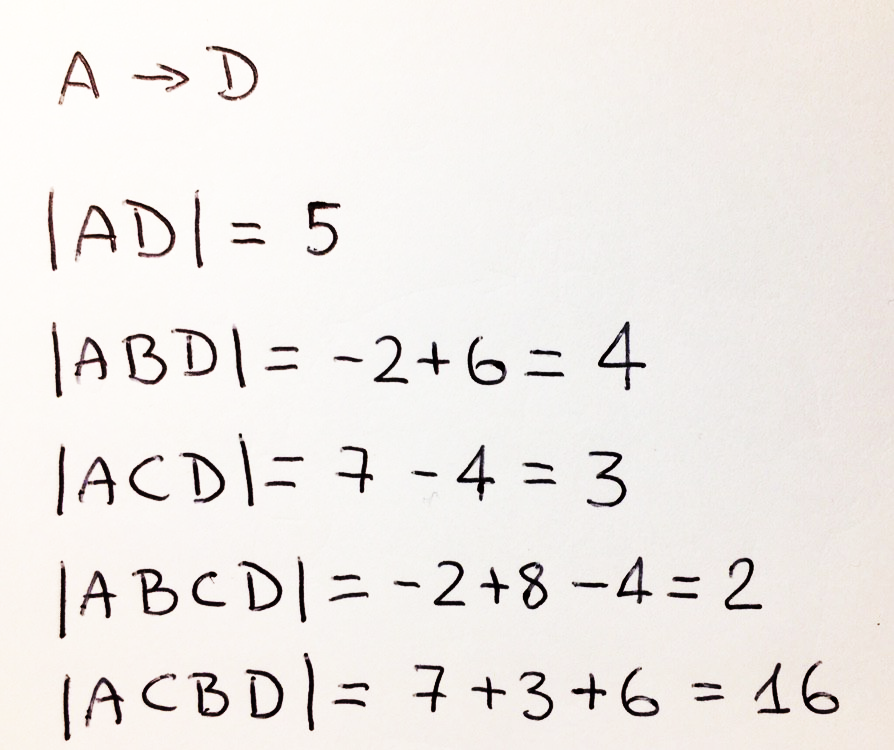, A D:

, A D , h(A) – h(D), , , ! , .

h, .

,

- S, . , S S* , S, «» .

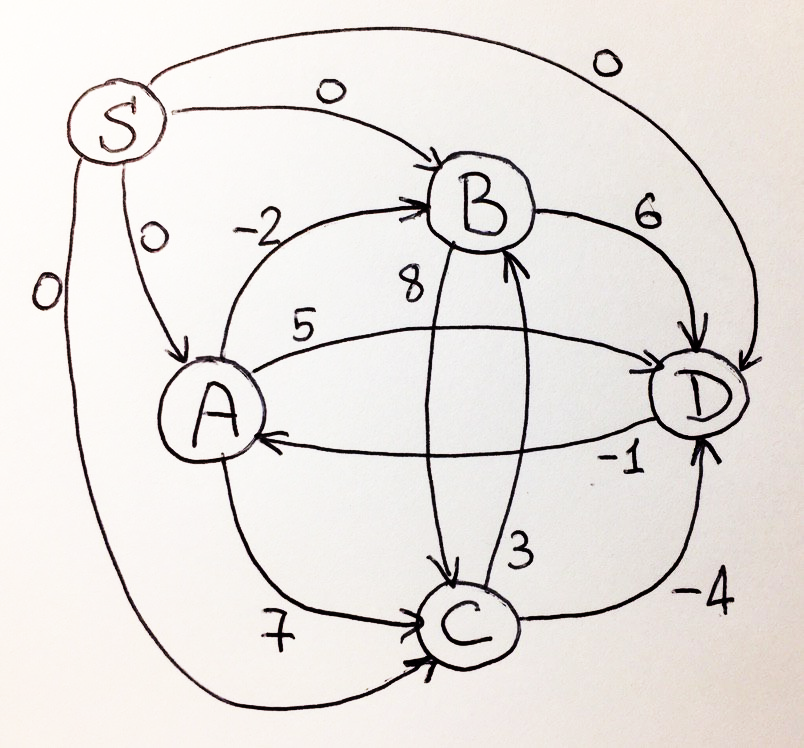
-, S . N «» S . «» , , :

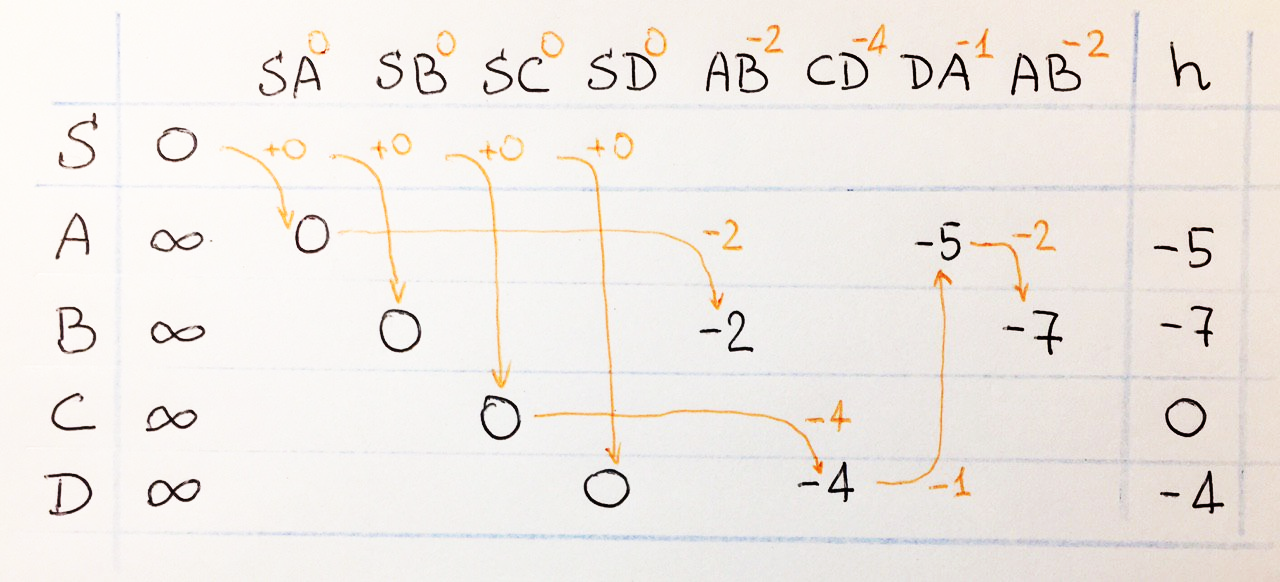
h . – S. S , h – . , , , , , , :

:

, , , ! .

, :

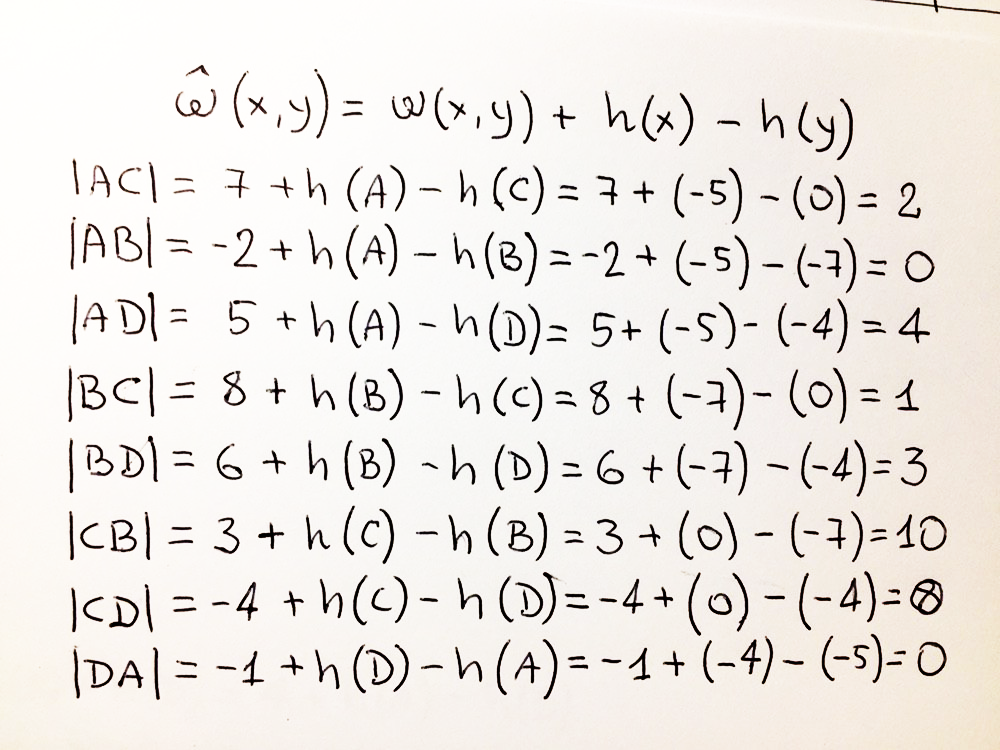
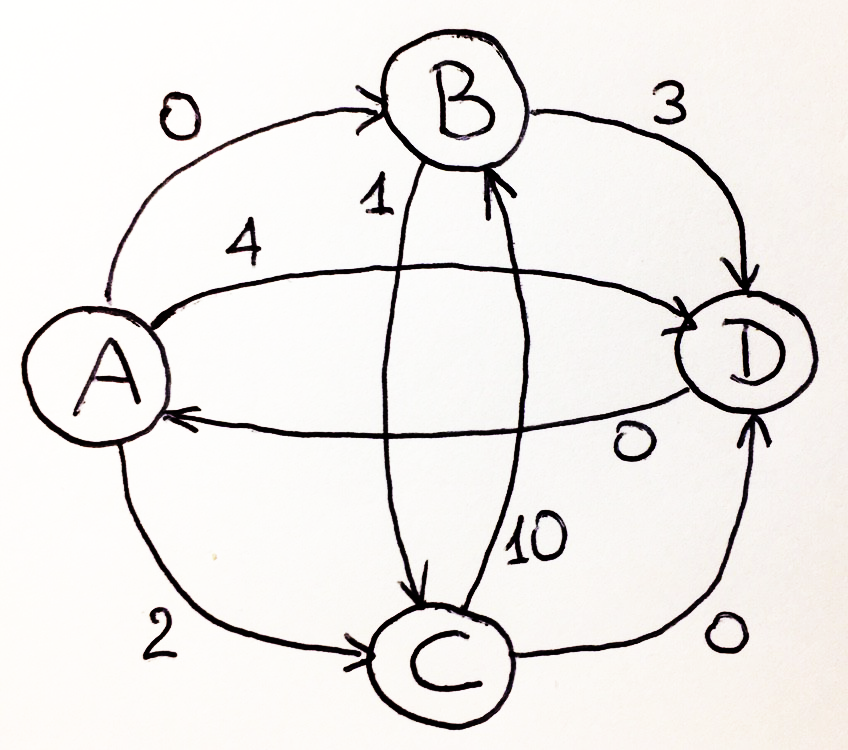
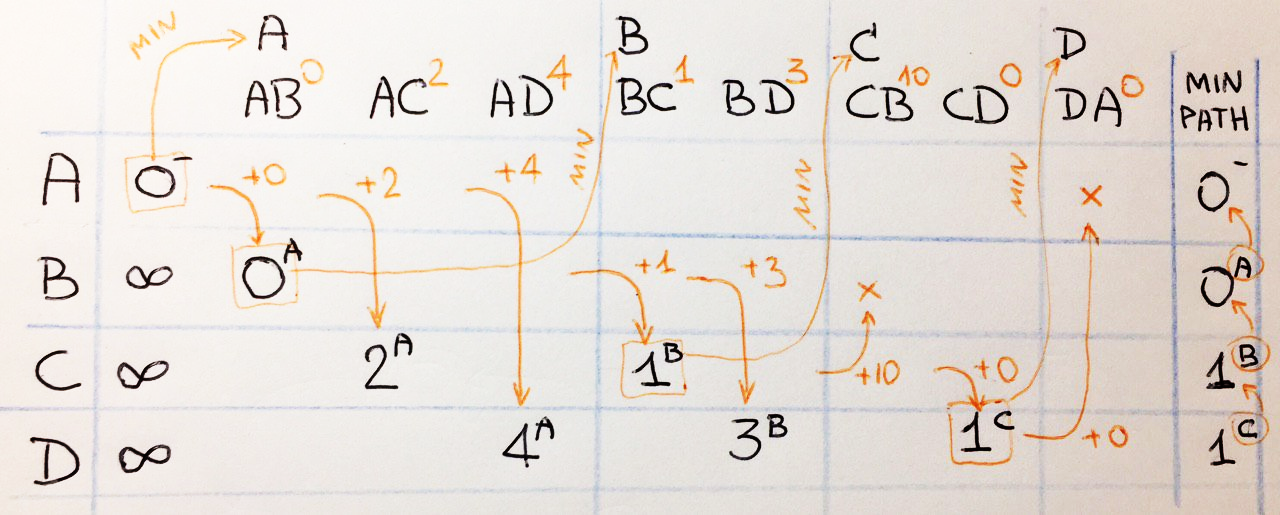
, , , . . , A D : A <= B <= C <= D, .

, . , .

---

« »

---