Quantencomputer und Kryptologie

Die Entwicklung der Computertechnologie bewegt sich in verschiedene Richtungen, nicht nur in die Phänomene der klassischen Physik, Elektronik, Optik und jetzt der Quantenmechanik.

Eine Bekanntschaft mit dem Problem der Quantenkryptologie und verwandten Themen (nicht nur in Veröffentlichungen) zeigte, dass es gewisse Mängel und Lücken in der Beschreibung und Darstellung gibt. Der Autor beschreibt die Besonderheiten eines bestimmten physikalischen Phänomens, eines Objekts, und ignoriert dessen Umgebung, selbst die nächstgelegene, die einen direkten Einfluss auf das Objekt hat (häufig ein störender Einfluss). Dies ist kein Vorwurf an die Autoren, ihr Recht zu präsentieren, wie sie es präsentieren. Es ist eher mein Motiv, mich dem allgemeinen Bewusstseinsstrom anzuschließen. Die materielle materielle Seite von Quantenphänomenen manifestiert sich auf die eine oder andere Weise, und das Ignorieren kann sich erheblich negativ auswirken. Was ist gemeint? Materialimplementierung von Quantencomputern (QCs), Registern, einzelnen Qubits - aus denen alle QCs bestehen. Benutzeraustausch der Ergebnisse über Kommunikationsnetze und schließlich Schutz,Die Integrität und Verfügbarkeit solcher Ergebnisse durch den Eindringling sind ebenfalls Probleme.

Quantenkryptologie und verwandte Themen

Eine neue Richtung der Physik - Quanteninformation - entstand an der Schnittstelle von Quantenmechanik, Optik, Informationstheorie und -programmierung, diskreter Mathematik, Laserphysik, Spektroskopie und umfasst Fragen der Quantenkommunikationssysteme, des Quantencomputers, der Quantencomputer, der Quantenteleportation und der Quantenkryptologie sowie der Dekohärenzprobleme und Spektroskopie einzelner Moleküle und Verunreinigungszentren.



Auch ohne die Kryptologie zu berühren, stützt sich die Quantenphysik auf eine so große Anzahl klassischer physikalischer Phänomene und verwendet sie, um ihre Konzepte und Phänomene zu beschreiben, die in der Schulphysik (und vielleicht in der Universitätsphysik) von fast jedem Konzept "galoppiert" oder sogar bestanden wurden vertraut) bedarf einer Erklärung aufgrund neuer Entdeckungen und Errungenschaften der letzten Jahre, was im Rahmen des Artikels praktisch unmöglich ist. Diese Materialauswahl ist jedoch das Problem des Autors, nicht des Lesers.



In der Theorie der Kryptologie (Kryptographie + kryptographische Analyse) können auch mehrere Entwicklungsperioden (Stadien) unterschieden werden. Alte symmetrische Kryptologie (Einzelschlüssel, beide Seiten des Kommunikationskanals verwenden denselben Schlüssel); asymmetrische oder Zwei-Schlüssel-Kryptologie (eine Nachricht wird mit einem öffentlichen Schlüssel verschlüsselt und mit einem anderen entschlüsselt - mit einem privaten). Schließlich,

Die nächste Stufe in der Entwicklung der Kryptologie umfasst die Gegenwart und begann mit der Realisierung der Möglichkeit, einen Quantencomputer (QC) und eine Quantenkryptologie aufzubauen.



Experten der klassischen Kryptologie haben verstanden und erkannt, dass ein solcher Computer ein leistungsfähiges Werkzeug für die kryptografische Analyse von Chiffren ist, mit dem in Sekundenschnelle eine klassische Chiffre jeder Stärke gebrochen werden kann. Aber sie sahen die andere (positive) Seite der Öffnungsmöglichkeiten - die Möglichkeit, Quantenkryptographie mit praktisch unzerbrechlichen Chiffren zu erstellen.



Die Idee der Quantenkryptographie wurde fast gleichzeitig mit der Idee geboren, Quantenobjekte für Berechnungen zu verwenden, dh mit der Idee, einen Quantencomputer und ein Kommunikationssystem unter Verwendung von Quantenkanälen zusammen mit herkömmlichen zu schaffen.

Der Quantenkanal des Kommunikationssystems und seiner Elemente

Wir leben bereits in der Welt der Quantennetzwerke, die sich über Tausende von Kilometern erstrecken und in den Weltraum hinausgehen. Der globale Markt für kommerzielle Quantenkommunikationssysteme wird von drei Unternehmen dominiert: dem chinesischen Unternehmen Qasky und QuantumCTek sowie dem Schweizer ID Quantique (seit 2001). Sie liefern praktisch das gesamte Spektrum an Lösungen und Komponenten, von Einzelphotonenquellen und -detektoren über Quantenzufallszahlengeneratoren bis hin zu integrierten Geräten. In Russland verband ein solches Netzwerk 2016 zwei Büros der Gazprombank, die sich in einer Entfernung von etwa 30 Kilometern voneinander befinden. Im selben Jahr startete die VR China den Satelliten QUESS - Quantum Experiments at Space Scale, der eine Quantenverteilung der Schlüssel über eine Entfernung von über 7600 km zwischen den Observatorien in Peking und Wien ermöglichte.

Quantenkommunikationskanalschema

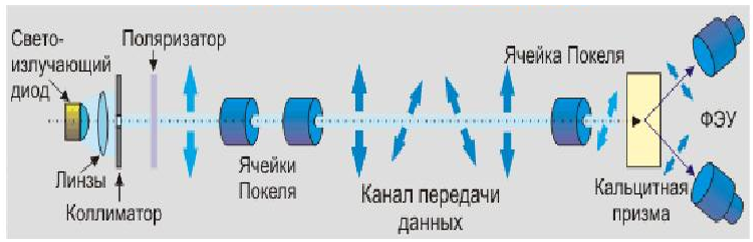
Abbildung 1. Schematische Darstellung eines Quantenkanal- und Quantenschlüsselverteilungsprotokolls



Die Idee und Implementierung der Quantenkryptographie ist in Abbildung 1 dargestellt. Im Bild links - der sendenden Seite der Nachricht, rechts - der empfangenden Seite. Wichtige notwendige Elemente des Systems sind Fotovervielfacher, die als Fotodetektoren fungieren, Pockels (Pockel) -Zellen, ein Calcitprisma (Wollaston) und ein Polarisator. Natürlich kann das System ohne den Rest der Elemente: eine Leuchtdiode, die auf einem Quantenpunkt (Laser), Linsen, Kollimator, Lichtleitfaser und Photonenfluss basiert, nicht aufgebaut werden, aber diese Elemente sind bekannt, werden seit langer Zeit und in vielen Systemen mit völlig unterschiedlichen Zwecken verwendet. Ein Quantenkanal mit Satelliten wird ohne Lichtwellenleiter implementiert.



Lassen Sie uns Erklärungen für einzelne Elemente der Schaltung geben.



Das Photon ist ein Elementarteilchen, ein Quantum elektromagnetischer Strahlung in Form von transversalen elektromagnetischen Wellen und ein Träger elektromagnetischer Wechselwirkung. Es ist ein masseloses Teilchen, das in einem Vakuum existieren kann, das sich nur mit Lichtgeschwindigkeit bewegt. Die elektrische Ladung des Photons ist ebenfalls Null. Ein Photon kann sich in nur zwei Spinzuständen mit einer Spinprojektion auf die Bewegungsrichtung (Helizität) ± 1 befinden. Myon ist das Quantum des Myonenfeldes. Das Photon ist ein Quantum des elektromagnetischen Feldes. In der Physik werden Photonen mit dem Buchstaben γ bezeichnet.



Leuchtdiode. Im Jahr 2001 entwickelten Andrew Shields und Kollegen von TREL und der University of Cambridge eine Diode, die einzelne Photonen emittieren kann. Dies ermöglichte es, polarisierte Photonen über große Entfernungen zu übertragen. Die experimentelle Demonstration konnte verschlüsselte Daten mit einer Geschwindigkeit von 75 Kbit / s übertragen - während mehr als die Hälfte der Photonen verloren ging.



Die Pockels-Zelle (manchmal auch Pockel-Zelle genannt) ist ein Kristall zwischen zwei gekreuzten Nikolen. Nicoli lässt kein Licht durch, wenn kein elektrisches Feld vorhanden ist, und wenn das Feld angelegt wird, erscheint eine Übertragung. Das äußere Feld (Kraftlinien) kann senkrecht zur Lichtausbreitung (Transversalmodulator) oder parallel (Längsmodulator) sein.



Der Pockels-Effekt (der Effekt ist nach F. Pockels benannt, der dieses Phänomen 1893 untersuchte) ist das Phänomen einer Änderung des Brechungsindex von Licht in Kristallen (optischen Medien), wenn es einem konstanten oder elektrischen Wechselfeld ausgesetzt wird. Es unterscheidet sich vom Kerr-Effekt dadurch, dass es im Feld linear ist, während der Kerr-Effekt quadratisch ist. Der Pockels-Effekt wird nur bei Kristallen beobachtet, die kein Symmetriezentrum haben: Aufgrund der Linearität sollte der Effekt das Vorzeichen ändern, wenn sich die Richtung des Feldes ändert, was in zentral symmetrischen Körpern unmöglich ist.



Der Effekt ist deutlich in Kristallen von Lithiumniobat oder Galliumarsenid zu sehen.

Der Pockels - Effekt, wie der Kerr - Effekt ist praktisch trägheits (Geschwindigkeit ca. 10 ^-10von). Aus diesem Grund findet es aktive Verwendung bei der Schaffung von optischen Modulatoren. Die praktische Umsetzung des Effekts erfolgt durch Pockels-Zellen.



Ein Quantenpunkt (QD) ist ein Miniaturstück aus Halbleitermaterial mit einem Durchmesser von 15 nm und einer Dicke von 5 Nanometern (nm), das bei Anlegen eines Stroms nur ein Paar Elektronen und Löcher einfangen kann.



Es gibt zwei Hauptmethoden zum Erstellen von Quantenpunkten:

1. Epitaxie ist eine Methode zum Züchten von Kristallen auf einer Substratoberfläche:
   
   
   
   
   • Molekularstrahl und Strahlenepitaxie;
   • Gasphasenepitaxie;
2. Synthese in Kolloid, in der Substanzen in Lösung gemischt werden.

Die kolloidale Synthese kann verwendet werden, um Nanokristalle zu erhalten, die mit einer Schicht adsorbierter oberflächenaktiver Moleküle beschichtet sind. Somit sind sie nach der Modifikation in organischen Lösungsmitteln löslich - auch in polaren Lösungsmitteln.



Hauptsächlich werden Verbindungen aus den Gruppen der Elemente III (Ga, Al, In) und V (As, P, Sb) des Periodensystems gezüchtet - die Gruppen werden als AIII BV (oder A ₃ , B ₅ ) bezeichnet. Auf der Basis solcher QDs wurden Halbleiterlaser und Mikrowellentransistoren hergestellt.



Von besonderem Interesse sind fluoreszierende Quantenpunkte, die durch kolloidale Synthese erhalten werden, beispielsweise Quantenpunkte auf der Basis von Cadmiumchalkogeniden, die je nach Größe in verschiedenen Farben fluoreszieren. Das Phänomen ist in der Praxis sogar Kindern bekannt, da es in Mobiltelefonen weit verbreitet ist.



Physikochemische Eigenschaften von Quantenpunkten



Ein breites Absorptionsspektrum, das es ermöglicht, Nanokristalle unterschiedlicher Farben mit einer Strahlungsquelle anzuregen. Ein schmaler und symmetrischer Fluoreszenzpeak (ohne „Schwanz“ im roten Bereich wie bei organischen Farbstoffen beträgt die Halbwertsbreite des Fluoreszenzpeaks 25–40 nm), der eine reine Farbe liefert: 2 nm Punkte - blau, 3 nm - grün, 6 nm - rot.

Hohe Fluoreszenzhelligkeit (Quantenausbeute> 50%). Hohe Fotostabilität.



Funktionsweise eines Quantenkommunikationskanals (Systems). Einzelne Photonen der Leuchtdiode werden von der Linse fokussiert und passieren den Kollimator. Danach treten sie in die Polarisationsvorrichtung ein, wo sie mit einem Chiffrierschlüssel in die erforderliche Form (eine von 4 (|, -, \, /)) polarisiert werden. Die Photonen bewegen sich unter Beibehaltung der Polarisation entlang des Kanals des Kommunikationssystems und auf der Empfangsseite wieder durch die Pockels-Zelle. Danach fallen sie auf das Calcitprisma (Wollaston) und teilen einen einzelnen Photonenfluss in zwei Teile, wobei jeder auf seine eigene PMT gerichtet wird. Letztere lesen mit dem Chiffrierschlüssel Informationen und wandeln sie in eine Nachricht für den Empfänger um.

Voraussetzungen für Quantum Computing

Die Idee des Quantencomputers wurde 1980 von Yu. I. Manin [1] und 1982 in einem Artikel von R. Feynman [2] zum Ausdruck gebracht. Die Entstehung der Quantenmechanik, in deren Rahmen Ergebnisse erzielt wurden, die von der klassischen Mechanik unerklärlich sind, war der Anstoß für die Entwicklung nicht nur der Physik, sondern auch einer Reihe anderer wissenschaftlicher Bereiche, einschließlich Quantenkommunikation, Berechnung und Kryptologie.

Zur Beschreibung von Quantenkonzepten und -phänomenen bei der Berechnung und Manipulation von Variablen in Analogie zu einem digitalen Binärbit (Binärziffern = Bit) wird das Konzept eines Quantenbits eingeführt - ein Qubit.



Es werden auch verschiedene physikalische Modelle des Quantencomputers genannt: Ionenfallen, Photonen-Qubits, topologische Qubits usw.



Definition... Ein Qubit ist die kleinste Information, die in einem Quantencomputer gespeichert ist. Gemäß den Gesetzen der Quantenmechanik kann sich ein Qubit gleichzeitig in zwei Eigenzuständen befinden, die mit | 0⟩ und | 1⟩ bezeichnet sind.



Ein Qubit kann ein beliebiges zweistufiges Quantensystem sein, beispielsweise ein Quantenteilchen mit Spin ± ½ in einem konstanten Magnetfeld (Elektron, Kern, Photon). In diesem Fall kann der Zustand des Qubits durch die Überlagerung A | 0⟩ + B | 1⟩ spezifiziert werden, wobei A und B komplexe Zahlen sind, die die Bedingung | A | erfüllen ² + | B | ² = 1, d.h. das Teilchen geht mit Übergangswahrscheinlichkeiten | A | in einen der Eigenzustände über ² in 0 und | B | ² in 1. Die Technik des Rechnens mit Qubits wird ausreichend detailliert angegeben ( hier )



Die Amplituden der Wahrscheinlichkeiten werden durch die Formeln beschrieben: A = cos (½θ); B = -e ^iφ sin⁡ (½θ).

Qubit Konstruktion. Die Qualitätskontrolle kann mithilfe der planaren Nanometer-Technologie für integrierte Siliziumschaltungen erstellt werden. In diesem Fall müssen die Anforderungen zum Isolieren von Qubits von Freiheitsgraden, die zur Dekohärenz führen, erfüllt sein. Wenn wir Qubits als Spins auf einem Donor in einem Halbleiter betrachten, stellen Kernspins in der Matrix ein großes Reservoir dar, mit dem Donor-Spins interagieren können.



Die Spins in der Matrix müssen im Zustand I = 0 sein. Diese wichtige Anforderung schließt alle Halbleiter der AIII BV-Typen für die Matrixsynthese aus, da nur Silizium ein stabiles Isotop ^{28 aufweist}Si mit Spin I = 0. Eine weitere Anforderung ist die Tiefkühlung, die Temperatur muss so niedrig sein, dass eine Ionisierung des Donors ausgeschlossen ist. Eine wichtige Anforderung bei der Betrachtung von zwei oder mehr Qubits ist die Überlappung der Bereiche von Quanten-Schrödinger-Wellenfunktionen.



Der Donor für Si (Silizium) mit Spin I = ½ ist ein einzelnes ³¹ P (Phosphor) Atom . Für das ²⁸ Si: ³¹ P-System bei T = 1,5 K und einer niedrigen Konzentration von ³¹ P beträgt die Relaxationszeit des Elektronenspins etwa 1000 Sekunden und die Relaxationszeit des Kernspins ³¹P überschreitet 10 Stunden. Quantenberechnungen sind für Kernspins möglich, wenn sie auf einem positiv geladenen Donor in einer Halbleitermatrix lokalisiert sind. Ihre Temperatur sollte niedrig genug sein (3-5 Millikelvin), bei der eine Ionisierung des Donors ausgeschlossen ist.



Der Zustand eines Photons kann nicht zweimal gelesen (gemessen) werden. Ein Versuch, die Nachricht abzufangen, wird bemerkt. Bei der Identifizierung (Messung) des aktuellen Zustands eines Qubits {| 0⟩ oder | 1⟩} sollten die Zustände physikalisch unterscheidbar sein und durch Wahrscheinlichkeiten geschätzt werden. Solche Wahrscheinlichkeiten dienen indirekt dazu, den Anfangszustand (vor der Messung) des Qubits abzuschätzen. Qubits können als Einheitsvektoren in einem zweidimensionalen komplexen Vektorraum mit einer orthogonalen festen Basis {| 0⟩} und {| 1⟩} betrachtet werden. Die Quantenfeldtheorie betrachtet Teilchen als Schwingungen (Quanten) von Feldern. Das Photon ist ein Quantum des elektromagnetischen Feldes. Myon ist myonisch.



Eine Überlagerung von Zuständen ist so etwas wie eine Liste aller möglichen Zustände eines Quantenobjekts (sagen wir ein Photon). Bevor es gemessen wurde. Es ist keine Welle und kein Teilchen, sondern etwas anderes, das ähnliche Eigenschaften hat - „Welligkeit, Wavelet“.

Wenn mehrere Qubits (Qubit-Register) gleichzeitig betrachtet werden, führt eine Änderung des Zustands eines der Qubits zu einer Änderung des Zustands anderer. Sie ändern sich entsprechend der ersten.



Diese Verbindung wird als Verschränkung von Zuständen bezeichnet, und die Menge der Qubits wird als gefülltes Quantenregister eines Quantencomputers interpretiert. Dieses Register kann sich in verschiedenen Zuständen befinden und Austausch und subtile physikalische Abhängigkeiten zwischen Qubits implementieren.



Anforderungen an die Qualitätskontrolle



Die Anforderungen und allgemeinen Bedingungen für die Erstellung einer Festkörper-Qualitätskontrolle sind ebenfalls formuliert:

• «» ( );
• (100…1000Å) , , ;
• , (- );
• , () , ;
• , , ∆ = µgB, ∆N = =µNgNB, – , µ, µN – ; gN, g – g – ;
• () ;
• ( ), ;
• - - n- ;
• «» , , , , , CNOT π⁄8. .

Anforderungen an die Verarbeitung von Quanteninformationen und deren Übertragung (Austausch):



a) Das System muss in der Lage sein, in Form von stationären (rechnerischen) Qubits gespeicherte Daten zuverlässig in (übertragene) Netzwerk-Qubits (z. B. Photonen) umzuwandeln und umgekehrt.



b) Das System muss in der Lage sein, Netzwerk-Qubits zwischen Endpunkten korrekt zu übertragen.

Erstellung der Qualitätskontrolle und ihrer Elemente

Quantencomputer entwickeln sich rasant. QCs werden nach verschiedenen Prinzipien hergestellt: NMR - Kernspinresonanz, ESR - Elektronenspinresonanz, Kernspin in Silizium. Ein Teilchen, das ein Qubit erzeugt, kann ein Elektron, ein Kern, ein Photon sein, das den Spinzustand ändern kann.



Ein Quantencomputer (QC) ist ein Festkörpergerät (Halbleiterbauelement), das quantenphysikalische Phänomene und die Eigenschaften elektronischer (Kern-) Spins verwendet, um Berechnungen zur Lösung von Problemen durchzuführen



Es gibt viele Plattformen, auf denen ein universeller Quantencomputer aufgebaut werden kann. Jeder Ansatz hat jedoch seine Nachteile. Beispielsweise haben supraleitende Qubits im Vergleich zu anderen Realisierungen kurze Kohärenzzeiten, und es ist schwierig, einen großen Quantencomputer mit kalten Atomen aufzubauen.

Quantenpunkte sind eine vielversprechende Implementierung von Qubits, haben aber auch viele Probleme. Eine davon ist eine qualitative Messung von Qubits, die den Quantenzustand des Systems nicht zerstört. In diesem Zusammenhang werden einzelne Elektronen in Quantenpunkten als Qubits betrachtet, und die Zustände 0 und 1 werden durch den Elektronenspin beschrieben.

Ein Quantencomputer über Kernspins in Silizium

Die QC-Entwickler hatten etwas, worauf sie bei ihren Aktivitäten aufbauen konnten. Die nanoskalige planare Technologie für integrierte Siliziumschaltungen funktioniert, funktionale Anforderungen werden aufgelistet, Einschränkungen und Bedingungen werden größtenteils definiert. Das Si: ³¹ P-System wurde vor etwa 60 Jahren in Experimenten zur elektronen-nuklearen Doppelresonanz eingehend untersucht.





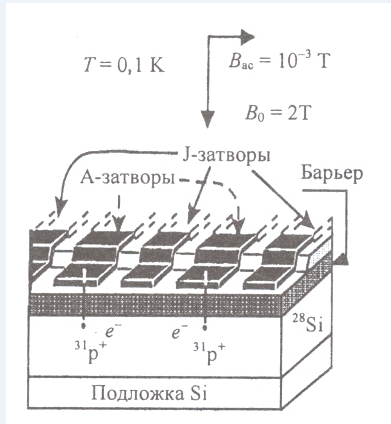
Abbildung A - Zwei Qubits in einem eindimensionalen Register (zwei ³¹ P- Donoren mit in ²⁸ Si eingebetteten gebundenen Elektronen )



Bei einer niedrigen Konzentration von ³¹ P und T = 1,5 K beträgt die Elektronenspinrelaxationszeit etwa 1000 s und die Kernspinrelaxationszeit ³¹ P. überschreitet 10 Stunden. Wenn die Temperatur ohne Ionisierung des Donors auf 0,1 K abfällt, konzentriert sich die Elektronenwellenfunktion auf den Donorkern, was zu einer hyperfeinen Wechselwirkung zwischen den Spins des Kerns und dem Elektron führt. Die Siliziumplatte wird in ein konstantes Magnetfeld Bo ≥ 2T gebracht.



Zwei Qubits in einem eindimensionalen Register enthalten zwei ³¹ P-Donoren mit in ²⁸ eingebetteten gebundenen ElektronenSi. Sie sind durch eine SiO ₂ -Schicht von den Kontrollmetalltoren auf der Oberfläche getrennt . A - Elektroden steuern (setzen) die Resonanzfrequenz des Kernspin-Qubits; J - Gates steuern die Wechselwirkung von Elektronen benachbarter Kernspins.

Elektronischer Spinresonanz-Quantencomputer

Bei Verwendung von ESD ist die Reinheit des Isotops der Siliziummatrix nicht kritisch. Für eine Reihe von Indikatoren ist ESR dem Kernspin vorzuziehen, ein Magnetfeld von 2 T (Tesla) liefert eine ESR-Frequenz von 56 GHz, und aufgrund der hohen Zeeman-Energie ermöglichen Elektronenspins den Betrieb bis zu Frequenzen im Gigahertz-Bereich. Nukleare Spins sind nur bis zu 75 kHz. Bei T = 1 K sind die Elektronenspins (im Gegensatz zu den Kernspins) vollständig polarisiert. Anstelle von Silizium werden Si / Ge-Heterostrukturen verwendet, die es ermöglichen, die effektive Masse des Donorelektronens zu steuern. J-Gates der Zellen sind nicht erforderlich. Für Messungen (Ablesen der Ergebnisse) können keine Einzelelektronentransistoren, sondern gewöhnliche Feldeffekttransistoren bei niedrigen Temperaturen verwendet werden.





Abbildung B - Darstellung der Methode zur Erfassung des Spinzustands eines Elektrons



Eine Person kann die Zustände von Qubits und Quantenregistern nicht direkt beobachten. Wenn eine Spannung an den beiden Elektronen angelegt , und der Gate - antiparallel (Singulettzustand) Rücken (links und rechts) mit einer und demselben Spender verbunden sind (D ^- Zustand) .They Übergänge in einem neuen Zustand ausführen kann, der einen elektrischen Strom erzeugt , dass gemessen mit einem kapazitiven Gerät (Einzelelektronentransistor). Dies stellt die Bestimmung des Spinzustands des Elektrons und des Donorkerns ³¹ P sicher. In diesem Fall wird das Pauli-Prinzip verwirklicht.





Figure C - Schema der Austauschwechselwirkung zwischen zwei Qubits (Zwei-Qubit-Betrieb)



Mit zunehmender Gate-Spannung nimmt die Bindungsenergie ab und der Bohr-Radius wasserstoffähnlicher Donoren nimmt zu. In der xy-Ebene können Elektronen elektrostatisch von einer der Barrieren angezogen werden, die durch B-Schichten der Zusammensetzung Si _0,23 Ge _{0,77 gebildet werden} . Das Coulomb-Potential nimmt ab V = -q / √ (r ² + d ² ), wobei r ² = x ² + y ² das Quadrat des horizontalen Abstands vom Donor und d der vertikale Abstand von der Barriere zum Donor ist.

In diesem Fall nimmt die Energie der Coulomb-Bindung von Elektronen ab und die Überlappung ihrer Wellenfunktionen nimmt zu, so dass Zwei-Qubit-Operationen ausgeführt werden können.



ESD-Design eines Qubits

Wir werden die Struktur der KK-Registerzelle für zwei Qubits betrachten. Die ESD-Materialzelle wird durch Züchten einer festen Si / Ge-Lösung auf einer Siliziumbasis (Kristall) erzeugt, auf der nacheinander 5 weitere Arbeitsschichten wachsen.





Abbildung E - Die Struktur der ESR-Zelle für zwei Qubits.



Links (a) - das Energieprofil der Ge _{1 - x} Si _x -Heterostruktur ; rechts (b) - Querschnitt einer Zwei-Qubit-Zelle. PT - Feldeffekttransistoren; <111> - Substratorientierung.



Die Hauptschichten sind T (Tuning) "Tuning" und D2-Donor ohne Unterbrechung der Leitungsbänder, wo Quantenberechnungen durchgeführt werden (zwischen Atomen 2000 Å). Die Dicke und Zusammensetzung der Schichten wird durch das Energiediagramm (links) und die Anforderungen an die Wirkung der Steuergatter (über den Schichten) bestimmt. Die T- und D2-Schichten sind zwischen den Barriereschichten (ihre Dicke beträgt 200 Å) eingeschlossen, die verhindern, dass sich Elektronen vertikal bewegen, sich in ihrer Zusammensetzung unterscheiden und einen anderen g-Faktor haben: g (T) = 1,563; g (D2) = 1,995 Elektronen der D2-Schicht spielen die Rolle von Qubits. Die Leitungsbandbrüche von 20 meV implementieren das Verbot und die Erhaltung von Qubit-Donorelektronen, sowohl Ladungsträgern als auch Quanteninformationen.





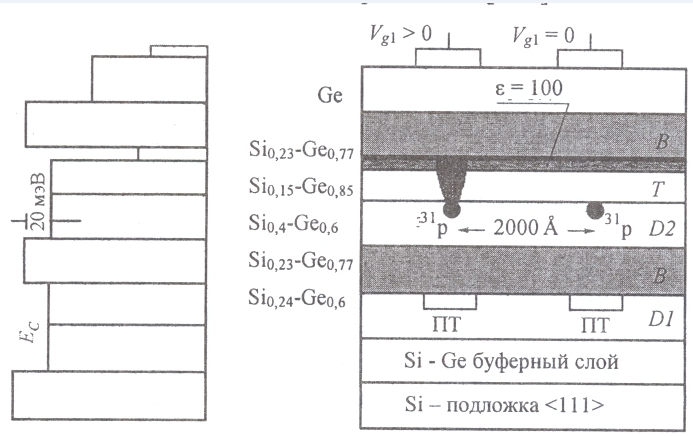
Abbildung E - ESD-Zellstruktur für zwei Qubits. Die Bezeichnungen der vorherigen Figur bleiben erhalten.



Berücksichtigen Sie den Effekt der Orientierung des kristallinen Siliziumsubstrats. Die mit dem Symbol (kristallographische Theorie) bezeichnete Orientierung des Substrats bietet mehrere Vorteile. Die Energie des Leitungsbandes ändert sich in dieser Richtung schneller. Feste Zusammensetzungen mit niedrigeren Spannungen können bei einer Barrierehöhe von etwa 50 meV ausgewählt werden, was im Vergleich zur [111] -Orientierung eine mehr als zweifache Zunahme darstellt.



Dementsprechend können die Barriereschichten bei gleicher Tunnelwahrscheinlichkeit dünner sein (Miniaturisierung), und die zulässigen Spannungen sind viel höher. höhere Dielektrizitätskonstante. Mit zunehmenden Entfernungen nimmt die Austauschfrequenz zwischen Qubits signifikant ab.



Für die QC basierend auf NMR an Phosphoratomen in Silizium wurde eine Lösung für ein ziemlich kompliziertes Problem bei der Erzeugung von Qubits gefunden - die genaue Anordnung der Donoratome (bis zu 100 Å).





Abbildung F - Diagramm des Aufbaus eines Registers aus NMR-Zellen von Qubits.



Das Diagramm der Anordnung einzelner Phosphoratome in Silizium ist dank der Fortschritte in der Nanotechnologie realisierbar geworden. Die Oberfläche des Siliziumwafers (Si 2 × 1), der unter Ultrahochvakuumbedingungen gereinigt wurde, wird mit einer Monoschicht aus Wasserstoff passiviert. Anschließend werden nach einem speziellen Programm mit Hilfe einer Rastertunnelmikroskopsonde einzelne Wasserstoffatome an bestimmten Stellen desorbiert. Danach wird Phosphindampf mit einem Druck von 10 bis ⁸ mm Hg in die Kammer eingeleitet. Kunst. Die adsorbierten Phosphinmoleküle dissoziieren dann bei einer Temperatur von 500 ° C und lassen die Phosphoratome an den Adsorptionsstellen an Silizium gebunden. Danach wird ein Überwachsen von Silizium bei niedriger Temperatur der resultierenden Struktur durchgeführt.



Es wird möglich, einen Computer zu erstellen, der auf der Ebene des gesamten Computergeräts parallel rechnen kann.



Lassen Sie uns die Faktoren und Fakten auflisten, die das Interesse an Qualitätskontrolle erhöht haben, und die Anreize für ihre praktische Entwicklung.



Für Quantencomputer wurden Algorithmen entwickelt, die schwierige Probleme lösen:

• Suche nach Gegenständen (Brute Force) in einer unstrukturierten Datenbank 1996 (LK Grover);
• Modellierung der Entwicklung von Quantensystemen, beispielsweise Kernreaktionen;
• Problem der Faktorisierung großer Zahlen (ZFBCH) 1994 (PW Shor);
• Berechnung des diskreten Logarithmus (DLOG) in einem endlichen Feld auf einer elliptischen Kurve;
• usw.

Ein Verfahren zur Steuerung von Quantenzuständen (Korrektur von Quantenfehlern) wurde entwickelt.



Ein Experiment, das Quantenberechnungen für den Grover-Algorithmus und andere zur Flüssigkern-Magnetresonanz-Qualitätskontrolle implementiert, wurde durchgeführt.



Auf Basis von Festkörperelementen wurden Varianten von CC-Strukturen erstellt:

• basierend auf Quantenpunkten (D. Loss, G. Burkard, L. Fedichkin, K. Valiev);
• basierend auf supraleitenden Josephson-Übergängen (DE Averin);
• auf den Kernspins von ³¹ P- Donorphosphoratomen in isotopenreinem ²⁸ Si (BEKane).
• auf den Elektronenspins der gleichen Phosphoratome in epitaktischen Heterostrukturen
• Ge1-x Sechs (D. DiVincenzo).

Nachfolgend finden Sie Formeln zur Schätzung der Qubit-Zustände und ihrer Wahrscheinlichkeiten.

Ein Quantenzustand ist jeder mögliche Zustand, in dem sich ein Quantensystem befinden kann. Ein reiner Quantenzustand kann beschrieben werden: 1) in der Wellenmechanik - eine Wellenfunktion; 2) in der Matrixmechanik - durch einen Vektor.



Quantencomputer versprechen, sich in unserer Welt stark zu verändern. Sie eignen sich naturgemäß gut für die Berechnungen, die zum Invertieren von Einwegfunktionen erforderlich sind. Für die symmetrische Kryptographie ist dies nicht so schlimm. Der Grover-Algorithmus zeigt, dass ein Quantencomputer Angriffe so stark beschleunigt, dass sich die effektive Schlüssellänge halbiert. Das heißt, ein 256-Bit-Schlüssel ist für einen Quantencomputer genauso komplex wie ein 128-Bit-Schlüssel für einen normalen Computer: Beide sind auf absehbare Zeit sicher.



Bei der Kryptografie mit öffentlichen Schlüsseln ist die Situation schlimmer. Shors Algorithmus bricht leicht alle gängigen Public-Key-Algorithmen, die sowohl auf Faktorisierung als auch auf diskretem Logarithmus basieren. Das Verdoppeln der Schlüssellänge erhöht die Schwierigkeit, achtmal zu knacken. Dies reicht für ein stabiles Funktionieren nicht aus (der Fehlerkorrekturmechanismus auf einem Quantencomputer kann für sie leicht zu einem unüberwindbaren Problem werden).



Verschlüsselung mit öffentlichem Schlüssel (wird hauptsächlich für den Schlüsselaustausch verwendet)

Das Schlüsselwort lautet hier "Schlüsselaustausch" oder, wie normalerweise gesagt, Schlüsselvereinbarung. Und die Verschlüsselung selbst (AES, "Grasshopper", "Magma" usw.) wird an symmetrischen Schlüsseln durchgeführt (natürlich mit einem periodischen Schlüsselwechsel, allen Arten von Keymeching-b, möglicherweise sogar Generierung für jedes Paket). Es geht nur um den Verschlüsselungsschlüssel.



In der Quantenphysik (Mechanik) gibt es eine Reihe von Prinzipien, die in der traditionellen klassischen Physik fehlen.



Nach dem Heisenbergschen Unsicherheitsprinzip ist es unmöglich, gleichzeitig die Koordinaten und den Impuls eines Teilchens zu erhalten. Es ist unmöglich, einen Parameter eines Photons zu messen, ohne einen anderen zu verzerren.

Das Ausschlussprinzip von Pauli besagt, dass zwei Elektronen (oder zwei andere Fermionen) nicht denselben quantenmechanischen Zustand in einem Atom oder einem Molekül haben können.



Mit anderen Worten, kein Elektronenpaar in einem Atom kann die gleichen Elektronenquantenzahlen haben. Das Prinzip verbietet das Klonen (Kopieren) von Qubits.

Das Klonen ist eine Operation für ein Paar oder mehrere Qubits, wodurch ein Zustand erzeugt wird, der ein Tensorprodukt identischer Zustände von Subsystemen ist.



Das Verbot des Klonens (Kopierens) ist eine Aussage der Quantentheorie, dass es unmöglich ist, eine ideale Kopie eines beliebigen unbekannten Quantenzustands eines Teilchens zu erstellen. Der Satz wurde 1982 von Wutters, Zurek und Dieck formuliert und war in den Bereichen Quantencomputer, Quanteninformationstheorie und verwandten Bereichen von immenser Bedeutung.



Der Zustand eines Quantensystems kann mit dem Zustand eines anderen Systems verknüpft werden. Beispielsweise können Sie einen verschränkten Zustand von zwei Qubits mithilfe einer Ein-Qubit-Hadamard-Transformation und eines Hardware-Zwei-Qubit-Quantengatters C-NOT erstellen. Das Ergebnis einer solchen Operation wird nicht geklont, da der resultierende Zustand nicht in der Sprache der Subsystemzustände beschrieben werden kann (der Zustand ist nicht faktorisierbar).





Die schwierige Frage ist, wie das Ergebnis zu interpretieren ist.



Vor- und Nachteile von Quantenkommunikation und Qualitätskontrolle gegenüber Klassik.



Positive Aspekte der Verwendung von Quantensystemen.

• QC arbeitet in Berechnungen nicht mit Zahlen, sondern mit Quantenzuständen;
• In der traditionellen (klassischen) Physik werden einzelne Teilchenzustände unter Verwendung einer gewöhnlichen skalaren Multiplikation von Vektoren kombiniert. in diesem Fall bildet die mögliche Anzahl von Zuständen von n Teilchen einen Vektorraum der Dimension 2 ⁿ ;
• () |0⟩ |1⟩ {|0⟩} {|1⟩}. . n ( n ) 2ⁿ. – {|0⟩ |1⟩} ; – {00, 01, 10, 11} . . ;
• m () 2^m . .
• .

Das Tensorprodukt von Zuständen ist die Ursache des EPR-Paradoxons und in gewissem Maße eine Erklärung dafür.

Tensorprodukt

Betrachten Sie den Fall von 2 Qubits.





Der Fall von 2 Qubits. Es gibt 4 Optionen für ihren gemeinsamen Zustand.



Diese 4 Vektoren in den Spalten der Tabelle sind im Raum von zwei Qubits grundlegend. Formal wird es wie folgt beschrieben. Wenn es Räume 1 und 2 mit den Dimensionen d1 und d2 und orthonormalen Basen {ei} und {fj} gibt, können wir einen Raum mit Basis {definieren$$$e_i⨂f_j$ }, wobei i Werte von 1 bis d1 und j - von 1 bis d2 annimmt.



Wenn wir das Skalarprodukt gemäß dem Gesetz auf dem neuen Raum einführen

$$$⟨e_i⨂f_j│e_m⨂f_n ⟩=⟨e_i│e_m ⟩⋅⟨f_j│f_n ⟩⟨e_i⨂f_j│e_m⨂f_n ⟩=⟨e_i│e_m ⟩⋅⟨f_j│f_n ⟩$

und setze es zu den anderen Vektoren fort, dann ist das Ergebnis ein Hilbert-Raum, der als Tensorprodukt von H1 und H2 bezeichnet und bezeichnet wird $$$_1⨂ _2$ . Offensichtlich ist seine Dimension d1d2.



Tensorprodukt der Bediener$$$_1 ϵ S(H_1 )$ und $$$_2 ϵ S(H_2 )$ Ist der Betreiber $$$_1⊗_2$ im Weltraum $$$_1⨂_2$nach dem Gesetz handeln ($$$_1⊗ _2 )|e_1⨂e_2 ⟩=( _1│e_1 ⟩ )⨂( _2│e_2 ⟩$). Es stellt sich die Frage, ob es einen Zustand im Raum gibt$$$_1⨂_2$kann definiert werden als das Tensorprodukt von Zuständen, die zu den Teilräumen H1 und H2 gehören?



Die Antwort auf diese Frage ist negativ, und ein klassisches Gegenbeispiel ist der Zustand im Raum von zwei Qubits$$$_1^2 ⨂_2^2$, EPR genannt durch die Anfangsbuchstaben der Nachnamen der Entdecker (Einstein, Podolsky, Rosen):



$$$|ψ_EPR ⟩= 1/√2 (|00⟩+|11⟩)$...



Es ist leicht zu erkennen, dass dieser Zustand nicht als Tensorprodukt von Einteilchenzuständen dargestellt werden kann:



$$$|ψ_EPR ⟩≠(a_1 |0⟩+b_1 |1⟩)⨂(a_2 |0⟩+b_2 |1⟩)$...

Quantenkryptologie

Die Quantenkryptographie (QCG) ist eine Kommunikationssicherheitsmethode, die auf den Prinzipien der Quantenphysik basiert. Im Gegensatz zur traditionellen Kryptographie, bei der mathematische Methoden verwendet werden, um die Vertraulichkeit von Informationen zu gewährleisten, konzentriert sich KKG auf physikalische Phänomene und berücksichtigt Fälle, in denen Informationen mithilfe von Objekten der Quantenmechanik übertragen werden.



Quantenkryptoanalyse (QCA). Die Verbreitung und Entwicklung der Quantenkryptographie hat zur Entstehung eines Gegengewichts geführt - der Quantenkryptoanalyse, die nach der Theorie in einigen Fällen Vorteile gegenüber dem Üblichen hat. RSA und andere zahlentheoretische Chiffren und kryptografische Methoden, die auf den Problemen der Faktorisierung großer Zahlen basieren, werden mit dem Aufkommen der Quanten-QCA ihre Stärke verlieren, wenn der diskrete Logarithmus gefunden wird.



Nach den Gesetzen der Physik kann der Zustand eines Lichtquants (Photon) nicht zweimal abgelesen werden: Nach der ersten Einwirkung auf das Photon ändert sich sein Zustand und ein zweiter Versuch führt zu einem anderen Ergebnis. Ein Versuch, Informationen abzufangen, wird bemerkt. Daher wird die Quantenkryptographie heute als die vielversprechendste Richtung der Verschlüsselung angesehen.



Um diese Probleme zu lösen, wurde insbesondere Shors Quantenalgorithmus (1994) entwickelt, der es ermöglicht, alle Primfaktoren großer Zahlen in einer endlichen und akzeptablen Zeit zu finden oder das Logarithmusproblem zu lösen und infolgedessen RSA- und ECC-Chiffren zu brechen. Daher ist der Aufbau eines ausreichend großen quantenkryptoanalytischen Systems eine schlechte Nachricht für RSA und einige andere asymmetrische Systeme. Es muss nur ein Quantencomputer erstellt werden, der den erforderlichen Algorithmus ausführen kann.



Ab 2012 konnten die fortschrittlichsten Quantencomputer 15 (in 150.000 Versuchen wurde die richtige Antwort in der Hälfte der Fälle gemäß Shors Algorithmus erhalten) und 21 faktorisieren.



Schutz von Informationen (Nachrichten) vor unbefugtem Zugriff und vor Änderungen mit Die Verwendung von Quantenobjekten wurde bereits 1970 von Steven Wiesner vorgeschlagen. Bennett S.N. und J. Brassard schlugen 10 Jahre später vor, diese Objekte zur Übertragung von Verschlüsselungsschlüsseln in Form von Quantenschlüsselverteilungsprotokollen zu verwenden - BB84 und später 1991 und 1992 ein verbessertes Protokoll.



Die Quantenkryptographie ist zusammen mit den Vorteilen und Vorteilen durch bestimmte Einschränkungen und negative Aspekte gekennzeichnet. Wie in jedem Kommunikationssystem in einem Kommunikationssystem, das Quantenkryptographie verwendet, gibt es Knoten mit Benutzern, die Geräte, Kommunikationskanäle, Energiequellen usw. empfangen und senden.



Die negativen Aspekte der Quantenkommunikation, die festgestellt werden, sind normalerweise die folgenden.



Komplexe Geräte müssen auf beiden Seiten (Senden und Empfangen) eines Kanals eines Quantenkommunikationssystems installiert werden:

• Unvollkommenheit der Quellen einzelner Photonen (niedrige Erzeugungsrate);
• Das Photonenpolarisationssteuersystem ist schlecht vor Interferenzen geschützt.
• Unvollkommenheit der Empfänger einzelner Photonen, empfindliche Detektoren arbeiten zusätzlich zu Photonen und auf anderen Teilchen;
• , ; ;
• 100 ( 100 ) , ( , , );
• ;
• ( $81000).

Um den Polarisationswinkel von Photonen zu messen, müssen Sie genau wissen, wie das Gerät an beiden Enden des Kanals ausgerichtet ist. Diese Bedingungen begrenzen die Verbreitung der Quantenkryptographie auf mobile Geräte.



Im Laufe der Zeit wurde eine akzeptable Option gefunden. Komplexe Geräte können nur von einem Benutzer an einem Ende des Kanals installiert werden. Ein anderer Benutzer akzeptiert das Signal und ändert nur den Zustand der Photonen, indem er seine Informationen zu den geänderten Zuständen hinzufügt. Die veränderten Photonen werden zurückgeschickt. Solche Geräte können bereits in ein Taschengerät passen.



Zur Festlegung der Ausrichtung der Geräte wird vorgeschlagen, Messungen in zufälligen Richtungen durchzuführen, und ihre Liste sollte offen veröffentlicht werden. Verwenden Sie für legitime Arbeit und Entschlüsselung nur Anweisungen, die den Abonnenten entsprechen. Die Methode wird als "Quantenschlüsselverteilung unabhängig vom Referenzrahmen" bezeichnet.

Quantenschlüsselverteilung

Die Quantenschlüsselverteilung (QKD) ist eine Schlüsselübertragungsmethode, bei der Quantenphänomene verwendet werden, um eine sichere Kommunikation zu gewährleisten. Diese Methode ermöglicht es zwei Parteien, die über einen offenen Kommunikationskanal von Glasfaser- oder freien Netzwerken verbunden sind, einen Photonenstrom zu übertragen, einen gemeinsamen Zufallsschlüssel zu erstellen, den nur sie kennen, und ihn zum Ver- und Entschlüsseln von Nachrichten zu verwenden.



Das Hauptziel der bekannten QKD-Protokolle (Quantum Key Distribution) besteht darin, zufällig übertragene Sequenzen von Partikeln (Photonen) abzugleichen.

1935 formulierten Einstein und eine Gruppe von Gleichgesinnten, die versuchten, die Kopenhagener Interpretation der Quantenmechanik in Frage zu stellen, ein Paradoxon, das später als Einstein-Podolsky-Rosen-Paradoxon bezeichnet wurde (EPR-Paradoxon-Tensormethoden beschreiben nicht alle Zustände von Qubits).



Unter den möglichen QKDs sind frühe BB84, B92 (Bennett), B91 (Eckert, ein anderer Name für EPR), später CW (kontinuierliche Variablen), das Schweizer COW-Protokoll (kohärente einseitige kohärente einseitige Verschlüsselung), Lo05 (erstellt von Lo H.-K. Ma K. und Chen K. 2005), SARG, Decoy State, DPS (Differential Phase Shift), mit Referenzzustand, Phasenzeit.

Charles H. Bennetts Algorithmus. Einige der aufgelisteten Protokolle werden nachstehend ausführlich erläutert.

Quantenprotokoll BB84

Beispiel 1 . Implementierung der Quantenverschlüsselungsschlüsselverteilung (BB84-Protokoll), die orthogonale Zustände von Quantenobjekten verwendet. Der Empfänger der Nachricht wirkt auf Objekte (Photonen) ein und wählt zufällig die Art der Messung aus: Er ändert entweder die lineare Polarisation des Photons (|, -) oder die diagonale (\, /)



UMSETZUNG DES QUANTUMPROTOKOLLS BB84





Lo05- und E91-Protokolle . Dieses Protokoll wurde 1991 von Arthur Eckert entwickelt. Es hat auch den Namen EPR (Einstein-Podolsky-Rosen), da es auf dem Einstein-Podolsky-Rosen-Paradoxon basiert. Lo05 ist ein quantenkryptografisches Schlüsselverteilungsprotokoll, das von den Wissenschaftlern von Luo H.-K. Mit der Quantenschlüsselverteilung (QKD) von Ma K. und Chen K. können zwei Benutzer, ein Sender und ein Empfänger, in absoluter Sicherheit in Gegenwart eines Eindringlings kommunizieren.



1991 schlug Bennett vor, den folgenden Algorithmus zu verwenden, um Änderungen von Daten zu registrieren, die unter Verwendung von Quantentransformationen übertragen wurden:

1. Der Sender und der Empfänger vereinbaren eine willkürliche Permutation von Bits in den Zeichenfolgen, um die Fehlerpositionen zufällig zu machen.
2. k (k , ).
3. . .
4. , , .
5. , , k.

Um festzustellen, ob unerkannte Fehler bestehen bleiben oder nicht, wiederholen der Empfänger und der Sender Pseudozufallsprüfungen, nämlich: Der Empfänger und der Sender kündigen offen die zufällige Vermischung der Positionen der Hälfte der Bits in ihren Zeichenketten an; Der Empfänger und der Absender vergleichen Paritäten offen (wenn sich die Zeichenfolgen unterscheiden, dürfen die Paritäten nicht mit der Wahrscheinlichkeit 1/2 übereinstimmen). Wenn es einen Unterschied gibt, verwenden der Empfänger und der Sender die binäre Suche und die Entfernung ungültiger Bits.



Wenn es keine Unterschiede gibt, erhalten Empfänger und Sender nach m Iterationen identische Leitungen mit einer Fehlerwahrscheinlichkeit von 2 ^{- m} .



Quantenprotokoll B92Ist eines der ersten Protokolle für die Quantenschlüsselverteilung, das 1992 vorgeschlagen wurde. C. Bennett. Daher der Name B92, unter dem dieses Protokoll heute bekannt ist. Das B92-Protokoll basiert im Gegensatz zu Protokollen wie E91 auf dem Prinzip der Unsicherheit. Informationsträger sind 2-Ebenen-Systeme, die als Qubits bezeichnet werden. Ein wichtiges Merkmal des Protokolls ist die Verwendung von zwei nicht orthogonalen Quantenzuständen.





Beispiel 2 . Implementierung der Quantenverteilung des Chiffrierschlüssels (B92-Protokoll), die orthogonale und nicht orthogonale Quantenzustände (Photonenpolarisationen) verwendet.





1. Im Fall einer EPR-Implementierung wählt der Sender zufällig eine Basis zum Messen des Zustands eines Photons aus einem EPR-korrelierten Paar, entweder linear oder kreisförmig.



2. Im zweiten Schritt hängen die Aktionen des Absenders von der Protokollversion ab.



a) wählt für die EPR-Implementierung eine zufällige Folge von Basen zum Messen der Polarisation von Photonen aus;



b) Der Sender wählt eine zufällige Folge polarisierter Photonen aus und sendet sie an den Empfänger.



3. Der Empfänger misst die Polarisationen der ankommenden Photonen unter Verwendung einer Folge zufälliger Basen.



4. Die Ergebnisse der Messungen des Empfängers (nicht ideale Quelle, Kommunikationskanal und Detektor führen zum Verlust von Photonen).



5. Der Empfänger informiert den Sender über die Basis zur Messung der Polarisation jedes empfangenen Photons.



6. Der Absender informiert den Empfänger darüber, welche Basen vom Empfänger korrekt ausgewählt wurden.



7. Der Sender und der Empfänger speichern die gemessenen Photonendaten in den richtigen Polarisationen und verwerfen alle anderen.



8. Der Rest der Daten wird gemäß der Codetabelle interpretiert:



9. Der Sender und der Empfänger überprüfen ihre Schlüssel auf die Paritätsübereinstimmung der ausgewählten Teilmenge von Bits. Wenn auch nur ein Bit anders ist, zeigt eine solche Prüfung die Existenz eines Eindringlings, der den Kanal abhört.



10. Seiten verwerfen eines der Bits der ausgewählten Teilmenge.

Als Ergebnis der Kommunikation unter dem B92-Protokoll erhalten der Sender und der Empfänger einen gemeinsamen geheimen Schlüssel 0101101 und zeigen die Abwesenheit eines Eindringlings mit einer Wahrscheinlichkeit von 1/2 an.

Quanten-COW-Protokoll

Beispiel 3 . Implementierung einer Quantenverschlüsselungsschlüsselverteilung (COW-Protokoll), die eine kohärente Einwegverschlüsselung verwendet.



Der Absender sendet "0" mit der Wahrscheinlichkeit (1 - f) / 2, "1" mit der Wahrscheinlichkeit (1 - f) / 2 und Kontrollzustände (Lockvogel) mit der Wahrscheinlichkeit f.



Der Empfänger gibt an, welche Bits der Sequenz er in der Timeline gemessen hat, und wenn der DM2-Detektor aufleuchtet, gibt er die Sequenz an den Sender zurück.



Der Absender führt aus (Key Sifting) - teilt dem Empfänger mit, welche Bits er von seinem Rohschlüssel ausschließen muss, da diese auf die Erkennung von Steuerzuständen zurückzuführen sind.



Absender. Bei der Analyse von Triggern in DM2 werden Kohärenzverletzungen anhand der Sichtbarkeit V1−0 und Vd bewertet und die Informationen des Eindringlings berechnet.



Fehlerkorrektur läuft. Stärkung der Geheimhaltung des gesiebten Schlüssels Korotkov und Jordanien geben eine



interessante Tatsache zum "Aufheben des Zusammenbruchs" der Wellenfunktion an .



Sie machten auf ihn aufmerksam und führten ein Experiment durch, das die Theorie testet und angeblich bestätigt. Aber anscheinend reicht eine Bestätigung nicht aus, und niemand hat irgendwelche Ideen oder Anwendungen über die Verwendung der Tatsache veröffentlicht. Ich konnte es einfach nicht verfehlen, dies zu erwähnen.

Aufhebung des Zusammenbruchs durch das Experiment (2008) der Nadav Katz-Gruppe, das die Richtigkeit der Korotkov-Jordan-Theorie (2006) bestätigt und den Zusammenbruch durch mehrfache Rückkehr des Qubit-Zustands vermeidet.

Im Allgemeinen überlagert jedes Quantensystem alle seine möglichen Zustände, bis eine Messung stattfindet und es einen der möglichen Zustände annimmt. Nach der Messung nimmt das System einen bestimmten Zustand an (Zusammenbruch).



Und so veröffentlichen Korotkov und Jordanien 2006 einen Artikel mit dem Titel "Auflösen der Wellenfunktion durch Rückgängigmachen von Quantenmessungen", der auf Russisch grob übersetzt werden kann als "Aufheben des Zusammenbruchs der Wellenfunktion durch Aufheben der Quantenmessung". oder arXiv: 0708.0365v1 [Quant-Ph:

Kryptoanalytische Schwachstellen, Angriffe, deren Klassifizierung

Experten glauben, dass die Verteilung von Quantenschlüsseln nicht für Hacking unverwundbar ist, aber für einen Eindringling durchaus zugänglich ist. Eine andere Sache ist, dass die Handlungen des Eindringlings erkannt werden können und der Schlüssel nicht beansprucht und durch einen anderen ersetzt wird. Spezifische Implementierungen solcher Systeme ermöglichen einen erfolgreichen Angriff und stehlen den generierten Schlüssel.



Eine ziemlich umfangreiche Liste von Angriffen ist möglich.



Angriffe auf Geräte eines Quantensystems:

• Verwendung eines Strahlteilers;
• unter Verwendung eines starken Impulses (Blenden von Lawinenphotodetektoren);
• Verwendung des Spektrums von Photonenquellen, wenn sie sich unterscheiden;
• die Verwendung eines PRNG durch den Rechtsverletzer ähnlich dem des Absenders.

Angriffe auf den Zustand von Quanten (Photonen):

• Kohärenz nutzen;
• kohärente Angriffe berücksichtigen Relaistaktiken;
• inkohärente Angriffe: Relais-Abfangjäger; unter Verwendung von Photonenklonierung;
• - kombinierte Angriffe:
  
  
  
  - Interaktion mit einzelnen Qubits;
  
  - Messungen ihrer Arrays.

Drei Beispiele für implementierte Angriffe (aus Veröffentlichungen im Netzwerk)

Strahlteilerangriff auf die Kuh

Es wird davon ausgegangen, dass die Ressourcen des Eindringlings unbegrenzt sind. Angriffe auf Schlüsselverteilungsprotokolle: Ein allgemeines Schema zum Vorbereiten und Messen von Quantenzuständen, ein Verfahren zum Erhalten von Ergebnissen von Messungen von Quantenzuständen eines Schlüssels auf der Seite von Sender und Empfänger. Angriffe auf die technische Implementierung von quantenkryptografischen Systemen (Quantenhacking).

• Dämpfung ⇒ µB = 10 - δl / 10µ;
• Strahlteiler + idealer Kommunikationskanal;
• µ max E = µ - µB = (1 - 10 - δl / 10) µ.

In der Februar-Ausgabe der Zeitschrift "Quantum Electronics" (unter den Gründern - den führenden Physikinstituten der Russischen Akademie der Wissenschaften) wird eine Methode beschrieben, wie man eine über ein Quantenkommunikationsnetzwerk übertragene Nachricht liest, die mit Schweizer Technologie implementiert wurde und unbemerkt bleibt. In dem Artikel heißt es: „Die Hauptidee des Angriffs besteht darin, einen Teil der abgefangenen Zustände einzeln zu messen und den Rest unverändert zu lassen. Die Autoren haben die optimalen Werte der Angriffsparameter für eine beliebige Länge des Kommunikationskanals berechnet. "



Die russische Entwicklung hat aufgrund einer speziellen Methode zur Übertragung mehrerer Kanäle über eine Leitung ein größeres Schutzpotential für die Schaffung von Mehrbenutzernetzwerken. Dies kann nach Ansicht des Entwicklers die Geschwindigkeit oder Bandbreite des Quantenkanals erheblich erhöhen.



Ein weiteres Beispiel ist der PNS-Angriff (Photon Number Splitting Attack) [1], der von Physikern aus Australien und Japan durchgeführt wurde, die zum ersten Mal eine zerstörungsfreie Quantenmessung eines Qubits durchführten, das aus einem Elektron in einem Quantenpunkt bestand. Wissenschaftler haben gezeigt, dass die Zuverlässigkeit einer solchen Messung über 99,6 Prozent liegt. Der Artikel wurde in Nature Communications veröffentlicht.



Wissenschaftler aus Australien und Japan unter der Leitung von Professor Seigo Tarucha vom RIKEN Science Center schlugen vor, ein Qubit in einem Quantenpunkt mit einem anderen mit einem Qubit verwickelten Elektron zu messen. Eine solche Implementierung ermöglicht es, den Zustand des Arbeits-Qubits für eine lange Zeit beizubehalten, was beispielsweise für die Implementierung von Fehlerkorrekturcodes erforderlich ist.



Um die zerstörungsfreie Anzeige zu testen, platzierten die Physiker zwei Elektronen in Si / SiGe-Quantenpunkten - eines der Elektronen als Arbeits-Qubit und das andere als Ancilla für die Messung. Die Wissenschaftler kontrollierten die Verbindung der Qubits mit einem Magnetfeld, das von einem Mikromagneten auf einem Chip erzeugt wurde.







Ein Diagramm der physikalischen Implementierung von zwei Qubits, die zwei Elektronen darstellen und von Wissenschaftlern in Quantenpunkten platziert wurden. J. Yoneda et al. - Nature Communications 11, 1144 (2020)



Literatur:



D. A. Kronberg, Yu I. Ozhigov, A. Yu Chernyavsky. Quantenkryptographie. - 5. Aufl. - MAKS Press, 2011 - S. 94-100. - 111 p. Archiviert am 30. November 2016

Bennett CH, Brassard G. Quantenkryptographie: Verteilung öffentlicher Schlüssel und Münzwurf // Tagungsband der Internationalen Konferenz über Computer, Systeme und Signalverarbeitung, Dez. 9-12, 1984, Bangalore, Indien. - IEEE, 1984. - S. 175

Bennett, CH und Brassard, G., Conf. über Computer, Systeme und Signalverarbeitung, Bangalore, Indien, 175-179 (1984).

Bennett CH Quantenkryptographie unter Verwendung von zwei beliebigen nichtortogonalen Zuständen // Phys. Rev. Lette. 1992. Vol. 68, 3121.

Ekert AK, Hutter B., Palma GM, Peres A. Abhören quantenkryptographischer Systeme // Physical Review A. - 1994. - Vol. 50. - S. 1047-1056

Einstein A., Podolsky B., Rosen N. Kann die quantenmechanische Beschreibung der physikalischen Realität als vollständig angesehen werden? // Phys. Rev. A - 1935. - Vol. 47, 777.

Shor PW-Schema zur Reduzierung der Dekohärenz im Quantencomputerspeicher // Phys. Rev. A 1995. Vol. 52, 2493.

Shor PW Polynom-Zeit-Algorithmen zur Primfaktorisierung und diskreten Logarithmen auf einem Quantencomputer // SIAM J. Sci. Statist. Comput. 1997. Vol. 26, 1484.

Shor PW, Preskill J. Einfacher Sicherheitsnachweis des BB84-Quantenschlüsselverteilungsprotokolls // Phys. Rev. Lette. 2000. Vol. 85, 44