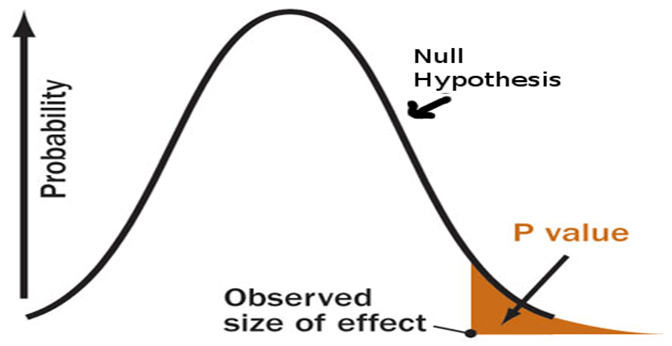
Zu der Zeit wusste ich nichts über p-Wert, Hypothesentest oder sogar statistische Signifikanz.
Ich habe beschlossen, das Wort "p-Wert" zu googeln, und was ich auf Wikipedia gefunden habe, hat mich noch verwirrter gemacht ...
Beim Testen statistischer Hypothesen ist der p-Wert oder Wahrscheinlichkeitswert für ein gegebenes statistisches Modell die Wahrscheinlichkeit, dass, wenn die Nullhypothese wahr ist, die statistische Zusammenfassung (zum Beispiel der absolute Wert der mittleren Differenz der Stichprobe zwischen zwei verglichenen Gruppen) größer oder gleich den tatsächlich beobachteten Ergebnissen ist.Gute Arbeit, Wikipedia.
- Wikipedia
Okay. Ich habe nicht verstanden, was p-Wert eigentlich bedeutet.
Als ich mich eingehender mit dem Bereich der Datenwissenschaft befasste, begann ich endlich zu verstehen, was p-Wert bedeutet und wo er in bestimmten Experimenten als Teil von Entscheidungswerkzeugen verwendet werden kann.
Deshalb habe ich mich entschlossen, den p-Wert in diesem Artikel sowie dessen Verwendung beim Testen von Hypothesen zu erläutern, um Ihnen ein besseres und intuitiveres Verständnis der p-Werte zu ermöglichen.
Wir können auch ein grundlegendes Verständnis anderer Konzepte und der Definition des p-Werts nicht verfehlen. Ich verspreche, dass ich diese Erklärung intuitiv gestalten werde, ohne Sie allen technischen Begriffen auszusetzen, auf die ich gestoßen bin.
Insgesamt enthält dieser Artikel vier Abschnitte, die Ihnen ein vollständiges Bild vom Erstellen eines Hypothesentests bis zum Verständnis des p-Werts und dessen Verwendung in Ihrem Entscheidungsprozess vermitteln. Ich empfehle Ihnen dringend, alle durchzugehen, um ein detailliertes Verständnis der p-Werte zu erhalten:
- Hypothesentest
- Normalverteilung
- Was ist ein P-Wert?
- Statistische Signifikanz
Es wird Spaß machen.
Lasst uns beginnen!
1. Hypothesen testen
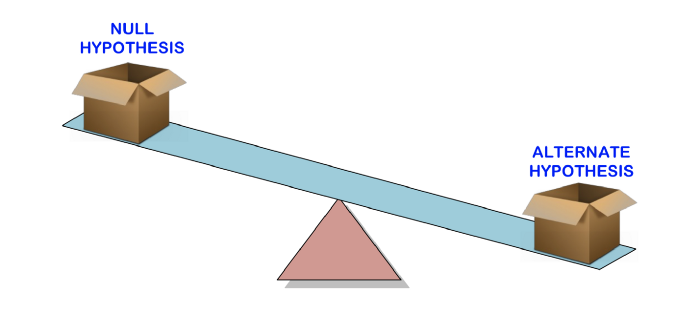
Bevor wir darüber sprechen, was p-Wert bedeutet, betrachten wir zunächst Hypothesentests , bei denen der p-Wert verwendet wird, um die statistische Signifikanz unserer Ergebnisse zu bestimmen.
Unser oberstes Ziel ist es, die statistische Signifikanz unserer Ergebnisse zu bestimmen.
Die statistische Signifikanz basiert auf diesen drei einfachen Ideen:
- Hypothesentest
- Normalverteilung
- P-Wert
Das Testen von Hypothesen wird verwendet, um die Gültigkeit einer Aussage (Nullhypothese) über eine Population unter Verwendung von Probendaten zu testen. Eine alternative Hypothese ist eine, die Sie glauben würden, wenn sich die Nullhypothese als falsch herausstellen würde.
Mit anderen Worten, wir erstellen einen Anspruch (Nullhypothese) und verwenden die Beispieldaten, um zu überprüfen, ob der Anspruch gültig ist. Wenn die Aussage nicht wahr ist, werden wir eine alternative Hypothese wählen. Alles ist sehr einfach.
Um herauszufinden, ob eine Behauptung gültig ist oder nicht, verwenden wir den p-Wert, um die Stärke der Beweise abzuwägen und festzustellen, ob sie statistisch signifikant sind. Wenn die Beweise die alternative Hypothese stützen, lehnen wir die Nullhypothese ab und akzeptieren die alternative Hypothese. Dies wird im nächsten Abschnitt erläutert.
Verwenden wir ein Beispiel, um dieses Konzept klarer zu machen, und dieses Beispiel wird in diesem Artikel für andere Konzepte verwendet.
Beispiel. Angenommen, eine Pizzeria behauptet, durchschnittlich 30 Minuten oder weniger Lieferzeit zu haben, aber Sie denken, dass sie länger als angegeben ist. Sie führen also einen Hypothesentest durch und wählen zufällig eine Lieferzeit aus, um den Anspruch zu testen:
- — 30
- — 30
- , , — — , .
In unserem Fall verwenden wir einen Einweg-Test , da es für uns nur wichtig ist, dass die durchschnittliche Lieferzeit 30 Minuten überschreitet. Wir werden diese Möglichkeit nicht in die andere Richtung betrachten, da die Konsequenzen einer durchschnittlichen Lieferzeit von weniger als oder gleich 30 Minuten noch vorzuziehen sind. Hier möchten wir prüfen, ob die durchschnittliche Lieferzeit mehr als 30 Minuten beträgt. Mit anderen Worten, wir wollen sehen, ob die Pizzeria uns betrogen hat.
Eine der gängigen Methoden zum Testen von Hypothesen ist die Verwendung des Z-Tests. Wir werden hier nicht auf Details eingehen, da wir besser verstehen wollen, was an der Oberfläche passiert, bevor wir tiefer tauchen.
2. Normalverteilung
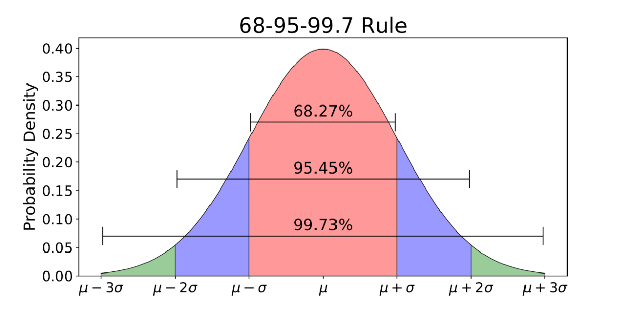
Die Normalverteilung ist eine Wahrscheinlichkeitsdichtefunktion , mit der die Verteilung von Daten angezeigt wird.
Die Normalverteilung hat zwei Parameter, den Mittelwert (μ) und die Standardabweichung, auch Sigma (σ) genannt.
Der Mittelwert ist der zentrale Trend in der Verteilung. Es definiert den Ort des Peaks für Normalverteilungen. Die Standardabweichung ist ein Maß für die Variabilität. Es bestimmt, wie weit die Werte vom Mittelwert abweichen.
Die Normalverteilung ist normalerweise mit der 68-95-99.7- Regel verbunden (Bild oben).
- 68% der Daten liegen innerhalb einer Standardabweichung (σ) vom Mittelwert (μ)
- 95% der Daten liegen innerhalb von 2 Standardabweichungen (σ) vom Mittelwert (μ)
- 99,7% der Daten liegen innerhalb von 3 Standardabweichungen (σ) vom Mittelwert (μ)
Erinnern Sie sich an die Fünf-Sigma-Schwelle für das Higgs-Boson, über die ich am Anfang gesprochen habe? 5 Sigma ist ungefähr 99,99999426696856% der Daten, die empfangen werden müssen, bevor Wissenschaftler die Entdeckung des Higgs-Bosons bestätigen. Dies war ein strenger Schwellenwert, um mögliche falsche Signale zu vermeiden.
Cool. Jetzt fragen Sie sich vielleicht: "Wie hängt die Normalverteilung mit unseren vorherigen Hypothesentests zusammen?"
Da wir den Z-Test zum Testen unserer Hypothese verwendet haben, müssen wir die Z-Scores berechnen (die in unserer Teststatistik verwendet werden), die die Anzahl der Standardabweichungen vom Mittelwert des Datenpunkts sind. In unserem Fall ist jeder Datenpunkt die Pizza-Lieferzeit, die wir erhalten haben. Beachten Sie, dass sich die Einheit auf der X-Achse von Minuten zu der Einheit der Standardabweichung ändert, wenn wir alle Z-Scores für jede Pizza-Lieferzeit berechnet und eine Standardnormalverteilungskurve wie unten dargestellt aufgezeichnet haben, während wir die Variable durch Subtrahieren des Mittelwerts und Teilen dividiert haben Es ist durch die Standardabweichung (siehe die obige Formel). Die Untersuchung der Standardglockenkurve ist nützlich, da wir Testergebnisse mit einer „normalen“ Population mit einer standardisierten Einheit in Standardabweichung vergleichen können, insbesondere wenn wir eine Variable haben, die mit verschiedenen Einheiten geliefert wird.

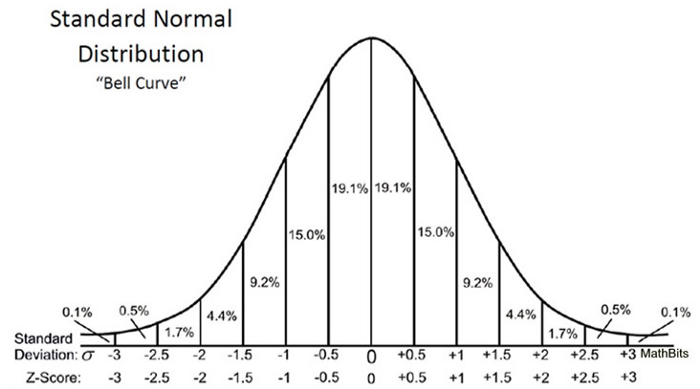
Der Z-Score kann uns sagen, wo die Gesamtdaten im Vergleich zur Durchschnittsbevölkerung liegen.
Ich mag die Art und Weise, wie Will Cursen es ausdrückt: Je höher oder niedriger der Z-Score, desto weniger wahrscheinlich ist ein zufälliges Ergebnis und desto wahrscheinlicher ist ein aussagekräftiges Ergebnis.
Aber wie hoch (oder niedrig) wird als überzeugend genug angesehen, um zu quantifizieren, wie wichtig unsere Ergebnisse sind?
Höhepunkt
Hier benötigen wir das letzte Stück, um das Rätsel zu lösen, den p-Wert, und prüfen, ob unsere Ergebnisse statistisch signifikant sind, basierend auf dem Signifikanzniveau (auch als Alpha bezeichnet) , das wir vor Beginn unseres Experiments festgelegt haben.
3. Was ist ein P-Wert?
Endlich ... Wir sprechen hier über den p-Wert!
Alle vorherigen Erklärungen sollen die Bühne bereiten und uns zu diesem P-Wert führen. Wir brauchen den vorherigen Kontext und die vorherigen Schritte, um diesen mysteriösen (eigentlich nicht so mysteriösen) p-Wert zu verstehen und wie er zu unseren Entscheidungen führen könnte, die Hypothese zu testen.
Wenn Sie so weit gekommen sind, lesen Sie weiter. Weil dieser Abschnitt der aufregendste Teil von allen ist!
Anstatt p-Werte anhand der Definition von Wikipedia (sorry Wikipedia) zu erklären, erklären wir es in unserem Kontext - Pizza-Lieferzeit!
Zur Erinnerung, wir haben zufällig einige Pizza-Lieferzeiten ausgewählt. Ziel ist es, zu überprüfen, ob die Lieferzeit 30 Minuten überschreitet. Wenn die endgültigen Beweise die Behauptung der Pizzeria stützen (die durchschnittliche Lieferzeit beträgt 30 Minuten oder weniger), werden wir die Nullhypothese nicht ablehnen. Ansonsten widerlegen wir die Nullhypothese.
Die Aufgabe des p-Werts ist es also, diese Frage zu beantworten:
Wenn ich in einer Welt lebe, in der die Lieferzeiten für Pizza 30 Minuten oder weniger betragen (die Nullhypothese ist richtig), wie unerwartet sind meine Beweise im wirklichen Leben?Der P-Wert beantwortet diese Frage mit einer Zahl - einer Wahrscheinlichkeit.
Je niedriger der p-Wert ist, desto unerwarteter sind die Beweise und desto lächerlicher sieht unsere Nullhypothese aus.
Und was machen wir, wenn wir uns über unsere Nullhypothese lächerlich fühlen? Wir lehnen es ab und wählen unsere alternative Hypothese.
Wenn der p-Wert unter einem bestimmten Signifikanzniveau liegt (die Leute nennen ihn Alpha, ich nenne dies die Schwelle der Absurdität - fragen Sie nicht warum, es ist für mich nur einfacher zu verstehen), dann lehnen wir die Nullhypothese ab.
Jetzt verstehen wir, was p-Wert bedeutet. Wenden wir dies in unserem Fall an.
P-Wert bei der Berechnung der Pizza-Lieferzeit
Nachdem wir einige Beispieldaten zu Lieferzeiten gesammelt haben, haben wir die Berechnung durchgeführt und festgestellt, dass die durchschnittliche Lieferzeit mit einem p-Wert von 0,03 10 Minuten länger ist.
Dies bedeutet, dass in einer Welt, in der die Lieferzeiten für Pizza 30 Minuten oder weniger betragen (die Nullhypothese ist korrekt), die Wahrscheinlichkeit, dass die durchschnittliche Lieferzeit aufgrund von zufälligem Rauschen mindestens 10 Minuten länger ist, bei 3% liegt. ...
Je kleiner der p-Wert ist, desto aussagekräftiger ist das Ergebnis, da es weniger wahrscheinlich durch Rauschen verursacht wird.
In unserem Fall verstehen die meisten Menschen den p-Wert falsch:
Ein p-Wert von 0,03 bedeutet, dass es eine 3% (prozentuale Wahrscheinlichkeit) gibt, dass das Ergebnis zufällig ist - was nicht wahr ist.Die Leute wollen oft eine eindeutige Antwort (ich selbst eingeschlossen), weshalb ich lange Zeit mit der Interpretation von p-Werten verwechselt wurde.
Der p-Wert * beweist * nichts. Es ist nur eine Möglichkeit, die Überraschung als Grundlage für eine intelligente Entscheidung zu nutzen.So können wir einen p-Wert von 0,03 verwenden, um kluge Entscheidungen zu treffen (WICHTIG):
- Cassie Kozyrkov
- Stellen Sie sich vor, wir leben in einer Welt, in der die durchschnittliche Lieferzeit immer 30 Minuten oder weniger beträgt - weil wir an Pizzeria glauben (unsere ursprüngliche Überzeugung)!
- Nach der Analyse der Lieferzeit der gesammelten Proben liegt der p-Wert um 0,03 unter dem Signifikanzniveau von 0,05 (vorausgesetzt, wir stellen diesen Wert vor unserem Experiment ein), und wir können sagen, dass das Ergebnis statistisch signifikant ist.
- , 30 , , , , .
- ? ( ) . , , , , , , .
- , — .
Inzwischen haben Sie vielleicht etwas herausgefunden ... Abhängig von unserem Kontext werden p-Werte nicht verwendet, um etwas zu beweisen oder zu rechtfertigen.
Meiner Meinung nach werden p-Werte als Werkzeug verwendet, um unsere anfängliche Überzeugung (Nullhypothese) in Frage zu stellen, wenn das Ergebnis statistisch signifikant ist. In dem Moment, in dem wir uns mit unserer eigenen Überzeugung lächerlich fühlen (vorausgesetzt, der p-Wert zeigt an, dass das Ergebnis statistisch signifikant ist), verwerfen wir unsere ursprüngliche Überzeugung (lehnen die Nullhypothese ab) und treffen eine intelligente Entscheidung.
4. Statistische Signifikanz
Schließlich ist dies die letzte Phase, in der wir alles zusammenfügen und prüfen, ob das Ergebnis statistisch signifikant ist.
Es reicht nicht aus, nur einen p-Wert zu haben, wir müssen einen Schwellenwert festlegen (Signifikanzniveau - Alpha). Alpha sollte immer vor dem Experimentieren eingestellt werden, um Verzerrungen zu vermeiden. Wenn der beobachtete p-Wert niedriger als Alpha ist, schließen wir, dass das Ergebnis statistisch signifikant ist.
Als Faustregel gilt, dass Alpha auf 0,05 oder 0,01 gesetzt wird (der Wert hängt wiederum von Ihrer Aufgabe ab).
Angenommen, wir setzen das Alpha vor Beginn des Experiments auf 0,05. Das Ergebnis ist statistisch signifikant, da der p-Wert von 0,03 niedriger als das Alpha ist.
Nachfolgend sind die Hauptschritte für das gesamte Experiment aufgeführt:
- Formulieren Sie die Nullhypothese
- Bilden Sie eine alternative Hypothese
- Bestimmen Sie den zu verwendenden Alpha-Wert
- Finden Sie den Z-Score, der Ihrem Alpha-Level zugeordnet ist
- Finden Sie Teststatistiken mit dieser Formel
- Wenn die Teststatistik kleiner als der Alpha-Z-Score ist (oder der p-Wert kleiner als der Alpha-Wert ist), lehnen Sie die Nullhypothese ab. Andernfalls lehnen Sie die Nullhypothese nicht ab.
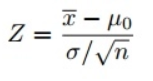
Wenn Sie mehr über die statistische Signifikanz erfahren möchten , lesen Sie bitte diesen Artikel - Erklärung der statistischen Signifikanz von Will Kersen .
Nachfolgende Überlegungen
Hier gibt es viel zu verdauen, nicht wahr?
Ich kann nicht leugnen, dass p-Werte für viele Menschen von Natur aus verwirrend sind, und es hat eine ganze Weile gedauert, bis ich die p-Werte wirklich verstanden und geschätzt habe und wie sie in unserem Entscheidungsprozess angewendet werden könnten. als Datenwissenschaftler.
Verlassen Sie sich jedoch nicht zu sehr auf p-Werte, da diese nur einen kleinen Teil des gesamten Entscheidungsprozesses unterstützen.
Ich hoffe, dass meine Erklärung der p-Werte intuitiv und hilfreich geworden ist, um zu verstehen, was p-Werte wirklich bedeuten und wie sie zum Testen Ihrer Hypothesen verwendet werden können.
Die Berechnung von p-Werten ist an sich einfach. Der schwierige Teil kommt, wenn wir p-Werte beim Testen von Hypothesen interpretieren wollen. Hoffentlich wird der schwierige Teil jetzt für Sie etwas einfacher.
Wenn Sie mehr über Statistik erfahren möchten, empfehle ich Ihnen dringend, dieses Buch zu lesen (das ich gerade lese!) - Praktische Statistik für Datenwissenschaftler, die speziell für Datenwissenschaftler geschrieben wurde, um die grundlegenden Konzepte der Statistik zu verstehen.

Erfahren Sie mehr darüber, wie Sie einen hochkarätigen Beruf von Grund auf neu aufbauen oder Ihre Fähigkeiten und Ihr Gehalt verbessern können, indem Sie an den kostenpflichtigen Online-Kursen von SkillFactory teilnehmen:
- Ausbildung des Data Science-Berufs von Grund auf (12 Monate)
- Analystenberuf mit jedem Startlevel (9 Monate)
- Machine Learning (12 )
- «Python -» (9 )
- DevOps (12 )
- - (8 )