Lineare Approximation einer Linienkombination durch eine Reihe von verrauschten Punkten

Formulierung des Problems

Betrachten wir das Problem der Approximation einer Kombination von Geraden durch einen Satz von verrauschten Koordinaten von Punkten, die sich auf einer bestimmten Kombination von Linien befinden (siehe Abb. 1 und Abb. 2). Die übliche Formel der linearen Approximation funktioniert hier nicht, da die Punkte gemischt sind und das Ergebnis eine gemittelte Linie zwischen ihnen ist (siehe Abb. 3).

Zahl: 1 Linienkombination und verrauschter Koordinatensatz

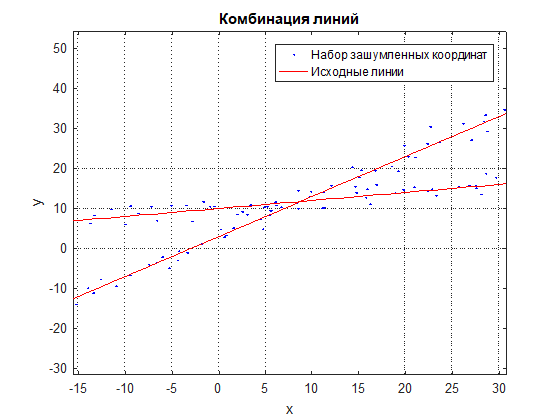
Zahl: 2 Eine Kombination aus Linien und verrauschten Koordinatensätzen in vergrößertem Maßstab

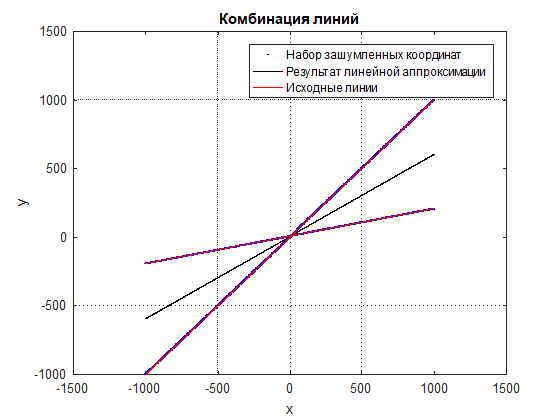
Zahl: 3 Ergebnis der linearen Approximation

Algorithmus

, , . .. , , -90 +90 ( -180 180 , .. ).

, , . , , . .

, , . , , .

1.

. , . , . -90 90 0.1 .

2.

, .

, , :

$$

$$y = kx + b, x_p, y_p$$

, , , :

$$

$$y-y_p=-(x-x_p)/k =>y= -x/k+ x_p/k+y_p$$

, :

$$

$$-x/k+ x_p/k+y_p=kx+b => -x+ x_p+ky_p= k^2 x+bk$$

$$

$$-bk+ x_p+ky_p= k^2 x+x => x= (x_p+ky_p-bk)/(k^2+1)$$

$$

$$y= k (x_p+ky_p-bk)/(k^2+1)+b= (〖kx〗_p+k^2 y_p-bk^2+bk^2+b)/(k^2+1)=(〖kx〗_p+k^2 y_p+b)/(k^2+1)$$

:

$$

$$dist= √((x_p- (x_p+ky_p-bk)/(k^2+1))^2+(y_p- (〖kx〗_p+k^2 y_p+b)/(k^2+1))^2 )$$

3.

, , , (. . 4-6).

. , (. . 7, 8). . 7 , .

. 4 ( )

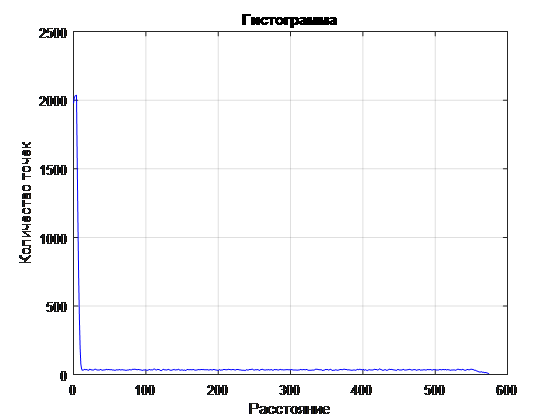
. 5 ( )

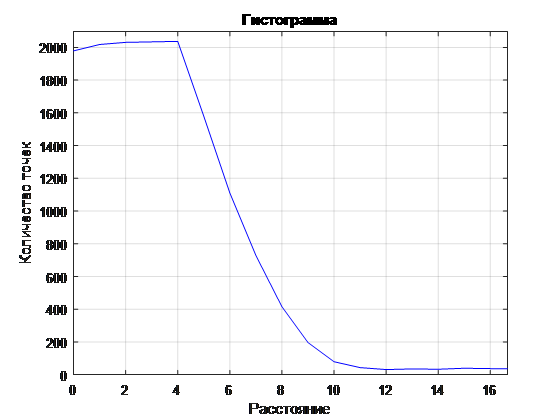
. 6 ( )

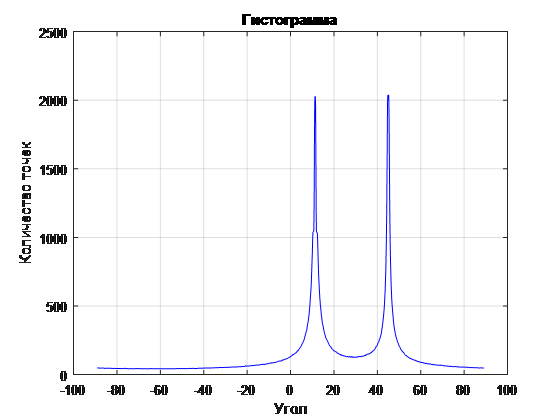
. 7 ( 1)

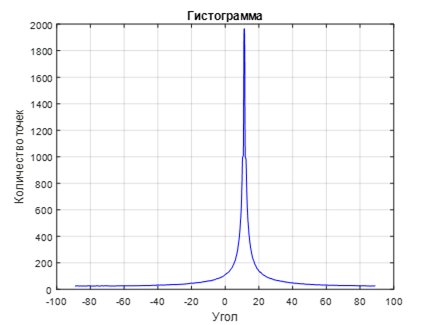
. 8 ( 2)

4.

, . , (. . 9 . 10):

$$

$$k= (N∑_1^N(xy)- ∑_1^Nx ∑_1^Ny)/(N∑_1^Nx^2 - (∑_1^Nx)^2 ); b =(∑_1^Ny-k∑_1^Nx)/N$$

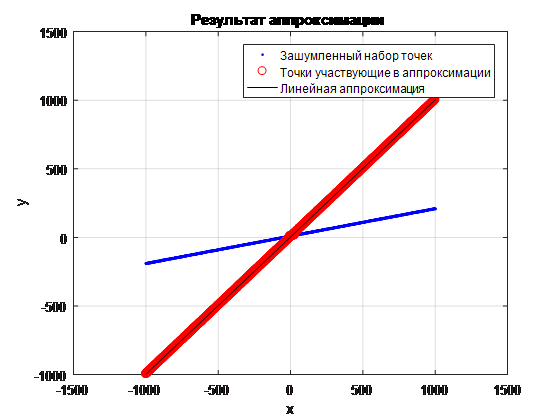
. 9

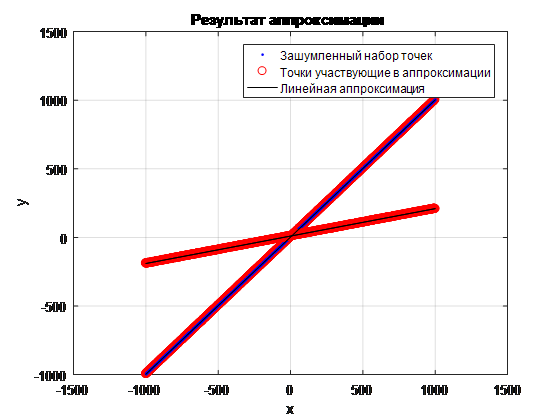
. 10

(. 11-13).

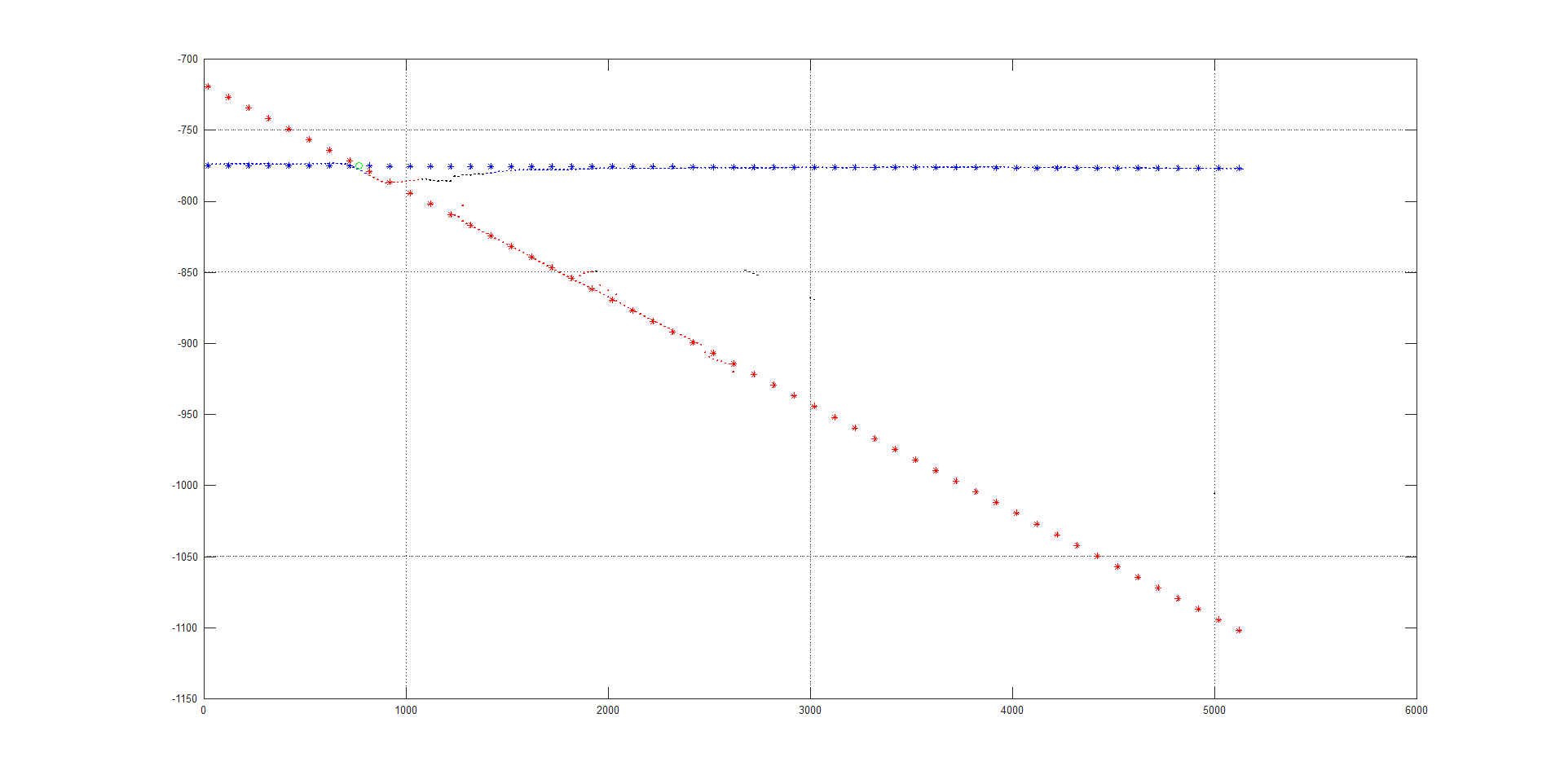
. 11

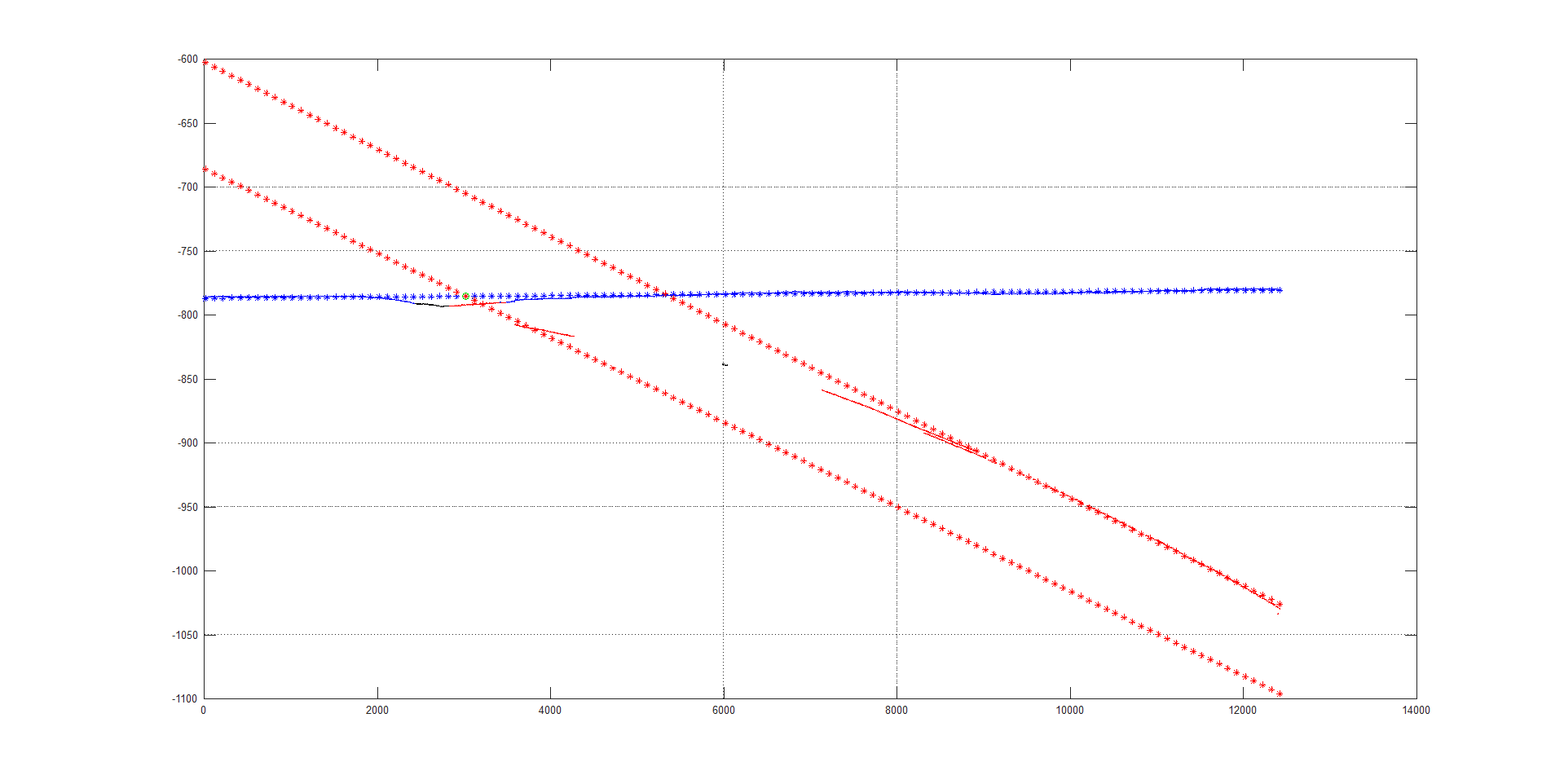
. 12

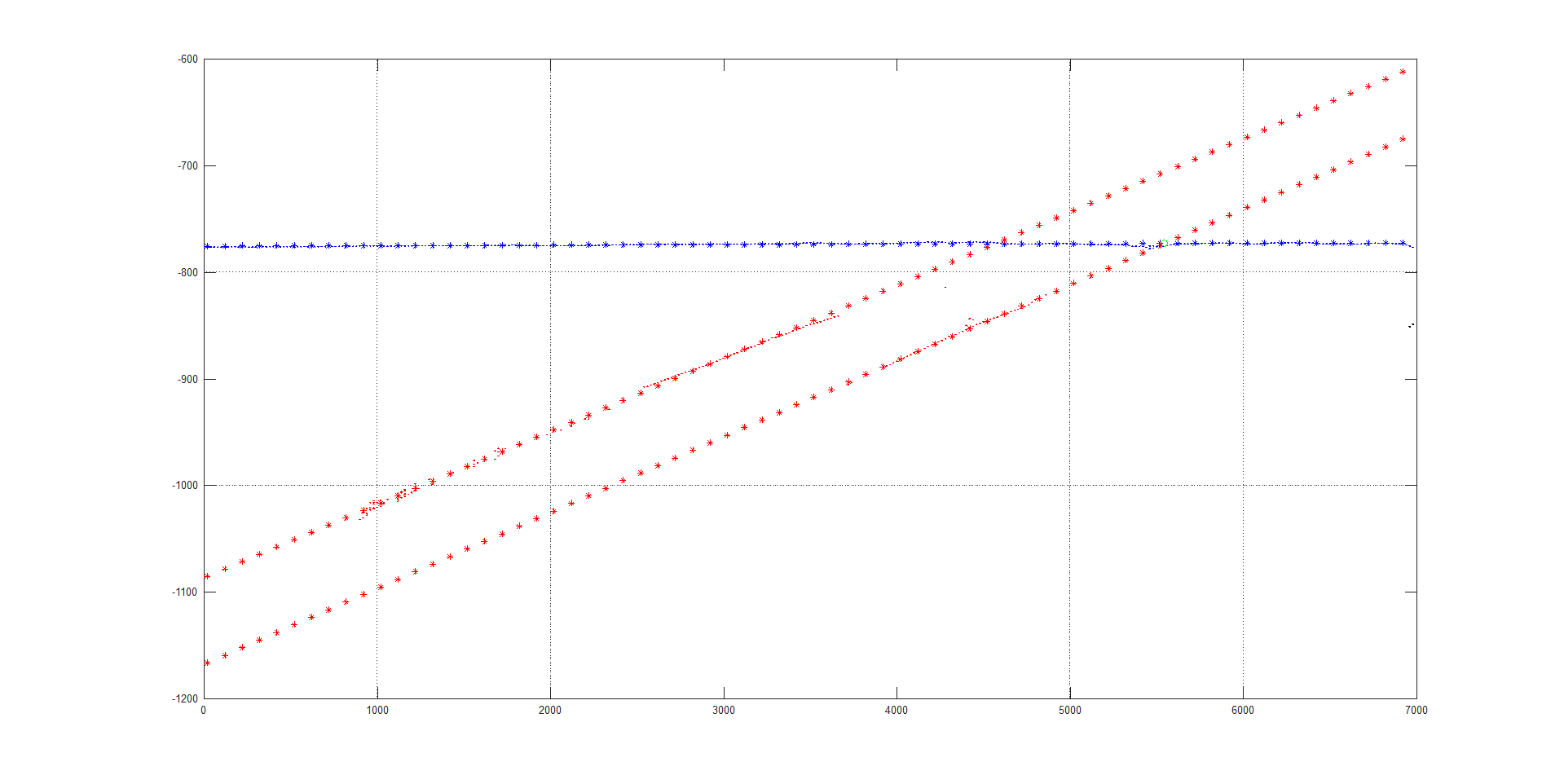
. 13

( ). .

, , , , .

, - . , . - , .