
Andere Artikel im Zyklus
AES — . I
ES — . II
AES — . III
AES — . IV
AES — . V.
ES — . II
AES — . III
AES — . IV
AES — . V.
Nach einer detaillierten Darstellung mit Details einzelner Transformationen, mit Elementen eines endlichen, nicht abstrakten (wie in vielen Veröffentlichungen, ohne das Chabrowski auszuschließen) algebraischen Feldes, sondern ( konkret ), in dem RIJNDAEL, AES-128 und ( Operationen des AES-128-Standards ausführen ) implementiert werden können wir über mögliche Angriffe auf die Chiffre nachdenken. Im Moment beschränken wir uns auf einen Angriff, unserer Meinung nach den verständlichsten und transparentesten (obwohl vielleicht nicht alle Leser) Habr.
Ich bin schon an die Nachteile gewöhnt, aber womit der Teufel nicht scherzt. Die Analyse möglicher Angriffe und erwarteter Ergebnisse wurde von vielen Autoren durchgeführt, aber konkrete erfolgreiche Beispiele oder einfach beeindruckende Designs reichen eindeutig nicht aus. Hier betrachten wir aus mathematischer Sicht einen Angriff unter Verwendung eines Fehlers, der vom Eindringling in den Chiffretext eingeführt wurde. Bei der Auswahl eines Angriffs für eine Demonstration versuchte der Autor, diejenigen nicht einzubeziehen, bei denen zu verdrehte und abstruse mathematische Dinge verwendet werden, aber das fragliche Thema selbst ist ziemlich ernst und erlaubt es nicht, zu Erklärungen an den "Fingern" überzugehen.
Ein wichtiges Ziel der Veröffentlichung ist es, die Anwendung der Mathematik aufzuzeigen, die die Grundlage von AES-128 bildet und die leider viele Autoren unbegründet und unbegründet umgehen oder falsch interpretieren, da nur wenige ihre Erfindungen überprüfen und darauf hinweisen können.
Das Material des Artikels ist nicht vollständig das ursprüngliche Konzept des Angriffs, die Hauptmaßnahmen stammen aus der Arbeit , aber es wurde von meinen Schülern sorgfältig ausgearbeitet, ergänzt und experimentell getestet. Sie haben sowohl in der höheren Algebra als auch in der Kryptologie gute Praxis.
1. Angriff auf den AES-Chiffrierschlüssel
Zunächst wird ein Angriff auf AES in einem einfachen Fall beschrieben, und dann wird klar, wie ein solcher Angriff verallgemeinert werden kann. Ziel des betrachteten Angriffs ist es, den Schlüssel K (Nr) der Chiffre wiederherzustellen. Sobald der partielle (runde) Schlüssel K (Nr) bestimmt ist, wird es leicht, den Schlüssel K zu erhalten.
1.1 Angriffsprinzip
Es wird angenommen, dass es möglich ist, durch Einfügen des Fehlers "& epsi;" in ein separates Byte der Matrix S des Zustands (eines von 16) nach der Operation ShiftRows (Nr - 1), d. H. Der vorletzten Runde, und dem Index (# der Zelle) des beschädigten Bytes (Elements) zu ändern ) Zustand. Diese letzte Hypothese kann weggelassen werden, sie wurde eingeführt, um den Angriffsmechanismus leichter zu erklären. Der neue Wert des Statuselements wird als unbekannt angenommen.
Der Fehler "ε" erstreckt sich auf nicht mehr als vier Bytes des Exit-Status des Prozesses. Für alle 4 veränderbaren Elemente des Ausgangszustands wird in Abschnitt 1.4 eine Reihe von Werten (Mengen) von Vektoren mit möglichem Fehler "ε" gefunden. Zusätzlich wird es möglich, die Mengen möglicher Werte "ε" (Definition 1) für diese vier Elemente zu schneiden. Wenn sich solche Mengen schneiden, wird eine kleinere Menge erhalten, und somit wird die Anzahl der für eine vollständige Analyse erforderlichen Chiffretexte verringert.
Schließlich drucken wir für jeden Fehler einige mögliche verstümmelte Werte für die vier Elemente des vorherigen runden Schlüssels aus. Wenn wir andere Chiffretexte bilden, finden wir vier Bytes des runden Schlüssels K (10). Dieser Angriff bleibt auch bei vielen allgemeinen Annahmen über den Ort des Fehlers erfolgreich. Zum Beispiel das Fehlen von Informationen über den Ort des Fehlers vor der 9. MixColumns () - Transformation. Der Unterschied zwischen der Chiffretextmatrix mit und ohne Verzerrungen zeigt die Verzerrungen und ihre Position (im Beispiel sind dies die Positionen 0,7,10,13).
Es wird auch angenommen, dass die in Runde 8 (vor der 8. MixColumns () - Transformation eingeführten "ε" -Fehler für die Analyse nützlich sein könnten. Gleichzeitig nimmt jedoch die Anzahl der für eine vollständigere Analyse erforderlichen Chiffretexte zu. Für das betrachtete numerische Beispiel werden ungefähr zehn Chiffretexte benötigt, um vier Bytes des Rundschlüssels K (10) zu erhalten, unter Bedingungen, bei denen die Hypothese bezüglich der Fehlerstellen nicht berücksichtigt wird.
1.2 Numerisches Beispiel für die Auswirkung eines Fehlers auf eine Nachricht
Hier wird das gleiche Beispiel verwendet, wie es im Anhang der genannten Arbeit angegeben ist . Die vorletzte und letzte Runde des Verschlüsselungsprozesses werden berücksichtigt (die Bytedarstellung der Daten hat die folgende Form):
Eingabe = '32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34 ';
Chiffrierschlüssel = '2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C';
Ausgang = '39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32 ';
Fehler "ε" = '1E 00 00 00 00 00 00 00 00 00 00 00 00'.
Das folgende Diagramm zeigt die in den Zustandsarrays enthaltenen Werte gemäß der Verschlüsselungsblocklänge und der Verschlüsselungsschlüssellänge von jeweils 16 Bytes (dh Nb = 4 und Nk = 4).
Die Fehlerausbreitung wird in Fett- und Hexadezimalschreibweise angezeigt. Nachfolgend sind die Plätze des Staates in verschiedenen Situationen aufgeführt:
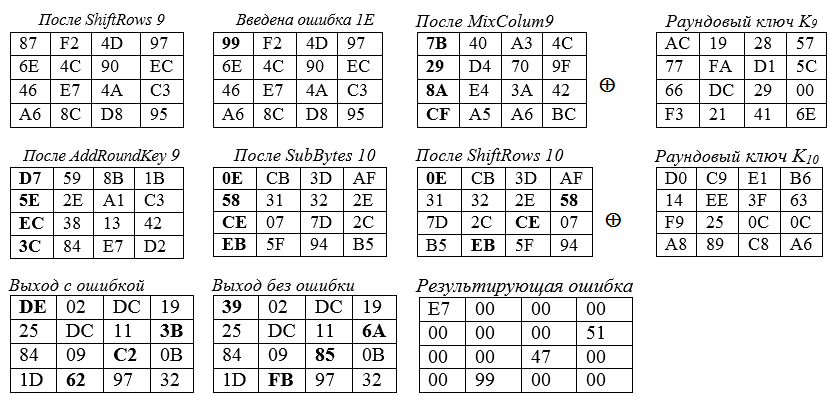
Der Fehler "ε" = 1E, der in das 0. Byte des Status der 9. Runde eingefügt wird, führt zu Änderungen in den vier Bytes des Endzustands. Beispiele für Berechnungen für die Eckzellen der Hauptdiagonale des "Quadrats" des Zustands:
- Der Fehler "ε" = 1E
87 ⊕ 1E = 1000 0111⊕ 0001 1110 = 1001 1001 = 99
wird in die obere linke (Eck-) Zelle des Zustandsquadrats der 9. Runde - unten rechts eingegeben Der Winkelzustand der 9. Runde nach MixColum9 wird mit dem Schlüsselbyte K (9) zusammengefasst:
BC ⊕ 6E = 1011 1100⊕ 0110 1110 = 1101 0010 = d2.
- Berechnung der Werte des resultierenden Fehlers.
Bei Vorhandensein von zwei Nachrichtentexten mit und ohne Fehler werden die Werte und Positionen der beschädigten Statusbytes durch Subtrahieren eines Textes vom anderen bestimmt. In unserem Fall kann eine solche Subtraktion durch Summieren der Texte Modulo 2 ersetzt werden. Wir erhalten ein Ergebnis ungleich Null nur für Bytes, die durch einen im Quelltext eingeführten Fehler geändert wurden.
Zum Beispiel finden wir in hexadezimaler Form die Fehlerwerte:
Tabelle 7 - Berechnung der Fehlerwerte

Als Ergebnis ergeben sich die Differenzfehler... Geben wir ein Beispiel für die Berechnung des letzten
Fehlerbytes : 62 ⊕ FB = 01100010 ⊕11111011 = 1001 1001 = 99. Die
Positionen der Statusbytes wurden durch den Fehler geändert
Geben Sie die Indizes für die Elemente des runden Schlüssels (letzte Runde) als K [0], K [7], K [10], K [13] an. Hier sind 0, 7, 10, 13 die Zellnummern der Zustandsmatrix, und die Matrix Ao ist die Transformationsmatrix zum Mischen der Spalten des Verschlüsselungsprozesses, deren erste Spalte die Form hat: '02', '01', '01', '03'.
Wie sich ein injizierter Fehler auf den Endzustand auswirkt

Analyse von Informationen, die erhalten werden, wenn ein Fehler auftritt
Die einzige Operation, die Informationen zum Schlüssel K (Nr) enthalten kann, ist die letzte SubBytes () - Transformation. Daher haben wir vier Gleichungen, wobei x0, x1, x2, x3, ε unbekannte Variablen sind.
Wir wollen Lösungen für die folgenden vier Gleichungen erhalten:
Bytes Durch einen Fehler modifizierte Informationen enthalten Informationen zu dem unbekannten Schlüssel, der diese Bytes generiert hat.
Alle diese Gleichungen können in einer einzigen Gleichung
s (x + cε) + s (x) = ε ', (1) verallgemeinert werden ,
wobei der konstante Wert =' 01 ',' 02 'oder' 03 'ist und diese Gleichung wir weiter lösen werden und analysieren.
Definition 1 . Der Satz von Lösungen von Gleichung (1) für Fehler & epsi; wird durch das Symbol B (c & epsi; ') bezeichnet und durch den Ausdruck definiert:
B (c & epsi;') = S (c & epsi; ') = {& epsi; F GF [2 8 ]: ∃ x є GF [2 8 ], s (x + cε) + s (x) = ε '}, | B (cε') | = 127.
Dies ist ein einzelner Fehlerbereich, der einem bestimmten Fehler ε 'entspricht. Für andere ε 'sind die Fehlerbereiche unterschiedlich.
Definition 2 . Betrachten Sie eine lineare Transformation ℓ über dem Feld GF (2):
ℓ: GF [2 8 ] → GF [2 8 ];
x → x 2 + x.
Das Bild von ℓ ist eine Abbildung des Im (ℓ) GF (2) -Vektorraums, d. H. Die Menge der Elemente
(x 2 + x) aus GF [2 8 ] bezeichnen wir mit 1 = Im (ℓ) und ihre Dimension dimGF (2) (E1) = 7. Wenn θ є 1, dann gibt es zwei verschiedene Lösungen x1, x2 є GF [ 2 8 ] Gleichungen x 2 + x = θ, und Lösungen erfüllen die Beziehung x2 = x1 + 1 und x2 ∙ x1 = θ (modd φx, (2 8 -1)) nach Vietas Theorem.
Die Variable θ ist ein freier Term einer quadratischen Gleichung.
Lassen Sie uns die betrachtete lineare Transformation anhand eines Beispiels veranschaulichen.
Beispiel Das GF-Feld ist gesetzt [2 8] wird die Transformation x → x 2 + x über ihre Elemente durchgeführt .
Tabelle 8 - das Anfangsfragment des Feldes GF [2 8 ] und die Ergebnisse der Transformation von Elementen.
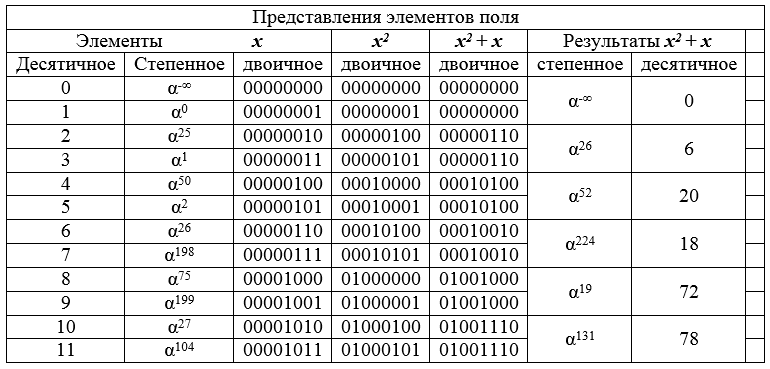
Tabelle 8 zeigt, wie die Konvertierung benachbarte Paare in einer dezimal geordneten Liste in dasselbe Feldelement ändert. Daraus folgt, dass das Ergebnis der Transformation (Bild) zweimal kleiner ist als das Vorbild (das Feld wird sozusagen um den Faktor 2 komprimiert). Dieses Prinzip der Kontraktion der Dimension von Mengen bildet die Grundlage des vorgeschlagenen Angriffs.

Satz 2 . Die folgende Aussage gilt für λ1, λ2 є GF [2 8 ] - {0}:





2. Verallgemeinerung und Implementierung
Zunächst werden mit Hilfe einer speziellen Softwareanwendung 20 fehlerhafte Chiffretexte generiert. Dazu werden der Quelltext, der Schlüssel und der Fehler in das Modell (Programm) eingegeben und die Positionsnummer, an der der Fehler platziert wird, festgelegt. Durch Drücken der Schaltfläche "Start" implementiert das Programm den Algorithmus und zeigt die Ergebnisse der letzten beiden Verschlüsselungsrunden in erweiterter Form für fehlerhaften Text, fehlerfreien Text und den Unterschied zwischen ihnen an. Danach wird der Chiffretext fehlerfrei und fehlerhaft gespeichert. Der Fehlerwert wird zyklisch geändert und durch Drücken der Schaltfläche „Start“ wird der nächste Chiffretext mit einem Fehler erhalten. Auf einem Wert der Spalte wurden 5 Chiffretexte mit einem Fehler gebildet.
Um einen Angriff auszuführen, müssen Sie eine Datei mit einem fehlerfreien Chiffretext und einen fehlerhaften Chiffretext mit dem Programm öffnen (die Daten in der Datei werden in hexadezimaler Form dargestellt). Die Chiffretexte und die Differenz zwischen ihnen werden als quadratisches Array von Bytes (Status) angezeigt. Durch Drücken der Taste „Nach Schlüssel suchen“ wird die Suche nach möglichen Bytes des Schlüssels gestartet. Der aktuelle Status der Prozesse wird in einem Textfeld angezeigt. Danach wird ein Chiffretext mit einem anderen Fehler geöffnet und der Vorgang wiederholt. Wenn ein Schlüsselbyte der Runde 10 empfangen wird, erscheint es auch im entsprechenden Quadratbyte-Array. Wenn alle 20 in der vorherigen Phase generierten Chiffretexte mit einem Fehler ausgeführt werden, besteht eine hohe Wahrscheinlichkeit, dass die Werte aller Bytes des Schlüssels der Runde 10 abgerufen werden (andernfalls werden auch Chiffretexte mit Fehlern benötigt).Stellen Sie danach den Verschlüsselungsschlüssel gemäß dem angegebenen Algorithmus "Wiederherstellung des Chiffrierschlüssels mit dem letzten Unterschlüssel" wieder herhier .
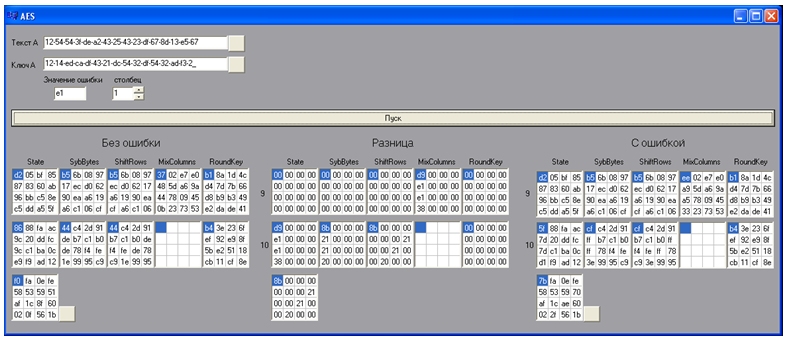
Abbildung 11 - Softwareprodukt zum Erstellen eines Chiffretextes mit einem Fehler
Um das Auflisten von Chiffretexten mit einem Fehler zu beschleunigen, können Sie ein Häkchen vor die Schaltfläche "Schlüssel suchen" setzen
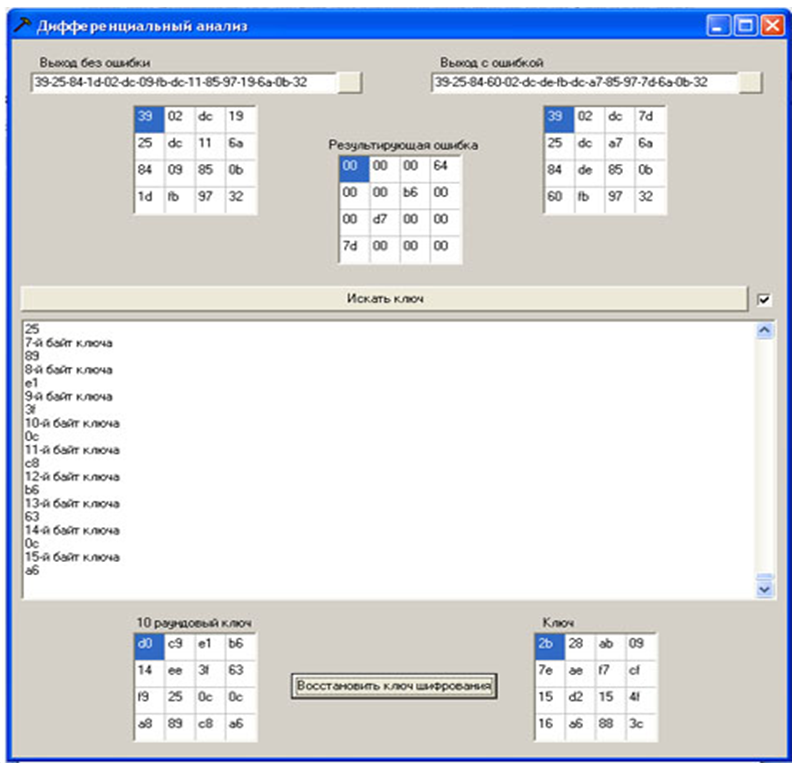
Abbildung 12 - Software - Implementierung des Angriffs
Ein Beispiel für das Software - Produkt - Betrieb: Der
Quellcode 3243f6a8885a308d313198a2e0370734
Key 2b7e151628aed2a6abf7158809cf4f3c
Fehler 1 1e000000000000000000000000000000
Ciphertext mit Fehler 1
Mögliche Bytes de25841d03bdc09


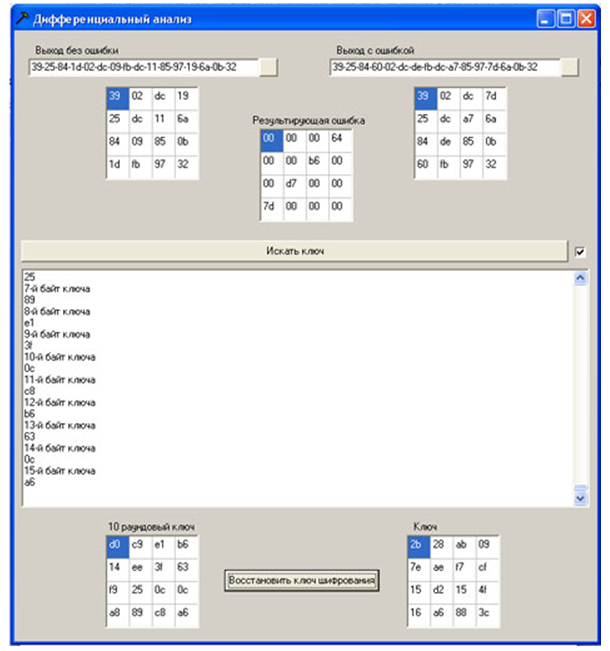
Abbildung 13 - Ein Beispiel für die Programmoperation
Schlüssel der Runde 10 d014f9a8c9ee2589e13f0cc8b6630ca6 Der Schlüssel wird vollständig wiederhergestellt. Der
wiederhergestellte Schlüssel 2b7e151628aed2a6abf7158809cf4f3c entspricht erwartungsgemäß dem in der Verschlüsselungssitzung angegebenen Schlüssel.
2.1. Situation, in der keine Fehlerortinformationen vorliegen
An dieser Stelle wird angenommen, dass der Fehler im Statusbyte zwischen den letzten beiden Ausführungen der MixColumns-Operation enthalten ist. Dies ist der gleiche Fall, mit der Ausnahme, dass der Fehler zwischen Bytes von 1 bis 16 eingeschlossen werden kann. Der Fehler wird mit der Operation MixColumns multipliziert und auf 4 Bytes Status verteilt.
Der erzwungene Fehler wird in der ersten Zeile der Differentialzustandsmatrix erzeugt. Hier kann anhand der erzwungenen Fehlerspalte ermittelt werden, zu welcher Spalte der eingegebene Fehler gehört. Dies erfolgt durch Untersuchen der vier möglichen Linienpositionen auf den eingegebenen Fehler unter Verwendung der in der vorhergehenden Beschreibung beschriebenen Methode.
2.2. Hardwaregerät
Nehmen wir an, Sie können ein AES-Hardwaregerät physisch stören. Lassen Sie uns zunächst mit einem AES-Gerät Chiffren für mehr als zehn zufällige Klartexte berechnen. Dann modifizieren wir das Beispielprojekt, indem wir die Linien ausschneiden und sie zeitlich zwischen den beiden Bytes während der Runde mit dem Boden (oder Vcc) verbinden, zwei Runden vor Abschluss. Immerhin haben wir ein Byte in Runde Nk -2, das immer durch '00' (oder 'FF') ersetzt wird.
Wir berechnen ein anderes Mal die gleiche Nachricht mit dem handelnden Gerät. Bei zufälligem Klartext ist ein fehlerhaftes Byte wie ein zufälliger Fehler. Dieser einzelne Fehler führt zu vier Fehlern in der Nk-1-Runde und sechzehn Fehlern in der Nk-Runde. In diesem Fall kann eine Abweichungsmatrix (Differential) erhalten werden, mit deren Hilfe durch Analyse des Fehlers der Schlüssel der letzten Runde gefunden werden kann.
Literatur:
[1] FIPS PUB 197: Advanced Encryption Standard, csrc.nist.gov/publications/fips/fips197/fips-197.pdf
[2] Boneh, DeMillo und Lipton, über die Bedeutung der Überprüfung kryptografischer Protokolle auf Fehler, Lecture Notes in Computer Science, Fortschritte in der Kryptologie, Verfahren von EU-ROCRYPT'97, pp. 37-51, 1997.
[3] E. Biham & A. Shamir, Differentialfehleranalyse geheimer Schlüssel-Kryptosysteme, CS 0910, Proceedings of Crypto'97.
[4] Ross J. Anderson, Markus G. Kuhn: Manipulationssicherheit - ein Warnhinweis, Der zweite USENIX-Workshop zu E-Commerce-Verfahren, Oakland, Kalifornien, 18.-21. November 1996, S. 1-11, ISBN 1-880446- 83-9.