🤜🏿 🕉️ 🤞🏻 Bayesianische Netzwerke mit Python

Haftungsausschluss: Dieser Artikel ist eine angepasste Übersetzung. Das Original kann hier gelesen werden .

Bayesianische Netzwerke mit Python - anhand von Beispielen erklärt

Aufgrund begrenzter Informationen (insbesondere in russischer Muttersprache) und Arbeitsressourcen sind die Bayes'schen Netzwerke von einer Reihe von Problemen umgeben. Und man könnte gut schlafen, wenn sie nicht in den meisten fortschrittlichen Technologien der Ära wie künstlicher Intelligenz und maschinellem Lernen implementiert wären.

Basierend auf dieser Tatsache widmet sich dieser Artikel ganz der Arbeit der Bayes'schen Netzwerke und wie sie selbst keine Probleme bilden können, sondern bei deren Lösung angewendet werden können, selbst wenn die zu lösenden Probleme äußerst verwirrend sind.

Artikelstruktur

Was ist ein Bayesianisches Netzwerk?
Was sind gerichtete azyklische Graphen?
Welche Mathematik liegt in Bayes'schen Netzwerken?
Ein Beispiel für die Idee eines Bayes'schen Netzwerks
Die Essenz des Bayes'schen Netzwerks
Bayesianisches Netzwerk in Python
Anwendung von Bayes'schen Netzwerken

Lass uns gehen.

Was ist ein Bayesianisches Netzwerk?

Bayesianische Netzwerke fallen in die Kategorie der probabilistischen grafischen Modelle (GPM). VGMs werden verwendet, um die Variabilität für die Anwendung in Wahrscheinlichkeitskonzepten zu berechnen.

Der gebräuchliche Name für Bayes'sche Netzwerke ist Deep Networks. Sie werden verwendet, um gerichtete azyklische Graphen zu modellieren.

Was sind gerichtete azyklische Graphen?

Ein gerichteter azyklischer Graph (wie jeder Graph in der Statistik) ist eine Struktur von Knoten und Verknüpfungen, wobei Knoten für einige Werte verantwortlich sind und Verknüpfungen Beziehungen zwischen Knoten widerspiegeln.

Acyclic == ohne gerichtete Zyklen. Im Kontext von Graphen bedeutet dieses Adjektiv, dass wir, wenn wir einen Pfad von einem Punkt aus beginnen, nicht das gesamte Diagramm des Graphen durchlaufen, sondern nur einen Teil davon. (Das heißt, wenn wir beispielsweise von Knoten 2 im Bild ausgehen, gelangen wir definitiv nicht zu Knoten 1).

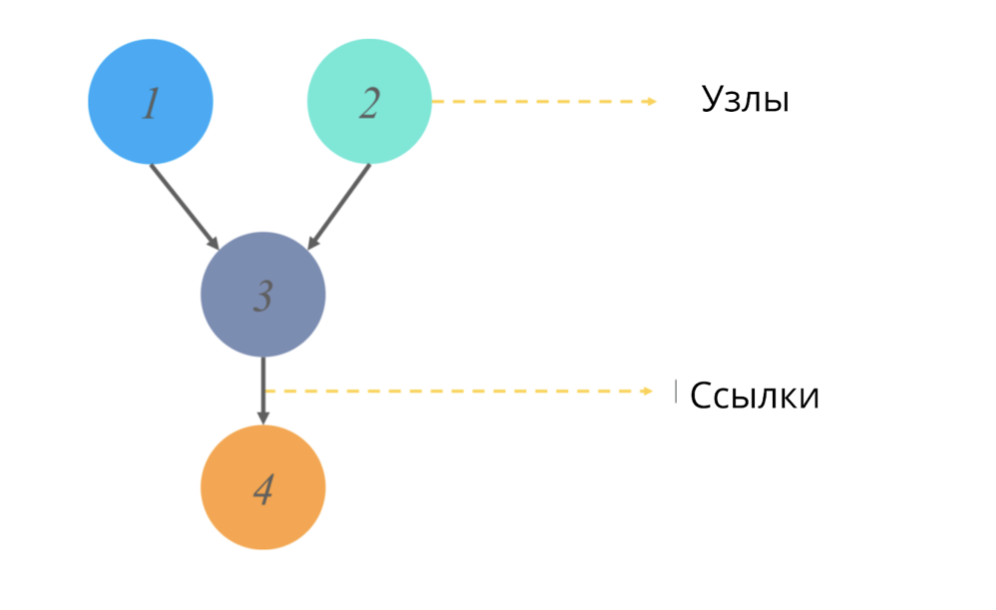
Was simulieren diese Diagramme und welchen Ausgabewert geben sie?

Modelle unsicherer gerichteter Graphen basieren auch auf einer Änderung des probabilistischen Ursprungs eines Ereignisses für jeden der Zufallswerte. Eine bedingte Wahrscheinlichkeitstabelle ist anwendbar, um jeden Wert darzustellen und zu interpretieren, und somit können wir die Verzweigung der Wahrscheinlichkeit von sequentiellen Ereignissen simulieren.

Alles ok. Zuerst war ich auch verwirrt. Lassen Sie uns zum besseren Verständnis die mathematische Komponente von Bayes'schen Netzwerken analysieren.

Bayesianische Netzwerkmathematik

Wie bereits in der Definition erwähnt, basieren Bayes'sche Netzwerke auf der Wahrscheinlichkeitstheorie. Bevor mit der Arbeit mit Bayes'schen Netzwerken begonnen wird, müssen daher zwei Fragen behandelt werden:

Was ist bedingte Wahrscheinlichkeit?

Was ist die gemeinsame mittlere Wahrscheinlichkeitsverteilung?

Bedingte Wahrscheinlichkeit Die

bedingte Wahrscheinlichkeit eines X-Ereignisses ist der numerische Wert der Wahrscheinlichkeit, dass das Ereignis X eintritt, sofern ein Ereignis Y bereits eingetreten ist.

Die Standardwahrscheinlichkeitsformel für einen Wert (im Artikel nicht angegeben): P (X) = n (x) / N, wobei n die untersuchten Ereignisse sind und N alle möglichen Ereignisse sind.

Für zwei Werte gelten die folgenden Formeln:

Wenn X und Y abhängige Ereignisse sind:

P (X oder Y) = P (X ⋂ Y) / P (Y), der Schnittpunkt der Wahrscheinlichkeit von X und Y / für die Wahrscheinlichkeit Y. (Das Vorzeichen "" im Zähler bedeutet den Schnittpunkt der Wahrscheinlichkeiten)

Wenn die Ereignisse X und Y unabhängig sind:

P (X. oder Y) = P (X), dh das Auftreten der untersuchten Ereignisse ist untereinander gleich wahrscheinlich.

Gemeinsame Wahrscheinlichkeit Die

gemeinsame Wahrscheinlichkeit ist die Definition eines statistischen Maßes für zwei oder mehr Ereignisse, die gleichzeitig auftreten. Das heißt, die Ereignisse X, Y und, sagen wir, C treten zusammen auf und wir reflektieren ihre kumulative Wahrscheinlichkeit unter Verwendung des Wertes P (X ⋂ Y ⋂ C).

Wie funktioniert das in Bayes'schen Netzwerken? Schauen wir uns ein Beispiel an.

Ein Beispiel, das die Essenz des Bayes'schen Netzwerks widerspiegelt

Angenommen, wir müssen die Wahrscheinlichkeit modellieren, eine der Noten eines Schülers für eine Prüfung zu erhalten.

Die Partitur besteht aus:

Prüfungsschwierigkeitsgrad (e): diskrete Variable mit zwei Abstufungen (schwer, leicht)
Schüler-IQ: diskrete Variable mit zwei Abstufungen (niedrig, hoch)

Der resultierende Bewertungswert wird als Prädiktor (Vorhersagewert) für die Wahrscheinlichkeit verwendet, dass ein Student oder eine Studentin die Universität betritt.

Die IQ-Variable wirkt sich jedoch auch auf die Zulassung zur Zulassung aus.

Wir repräsentieren alle Werte unter Verwendung eines gerichteten azyklischen Graphen und einer bedingten Wahrscheinlichkeitsverteilungstabelle.

Mit dieser Darstellung können wir eine kumulative Wahrscheinlichkeit berechnen, die aus dem Produkt der bedingten Wahrscheinlichkeiten von fünf Variablen gebildet wird.

Kumulative Wahrscheinlichkeit:

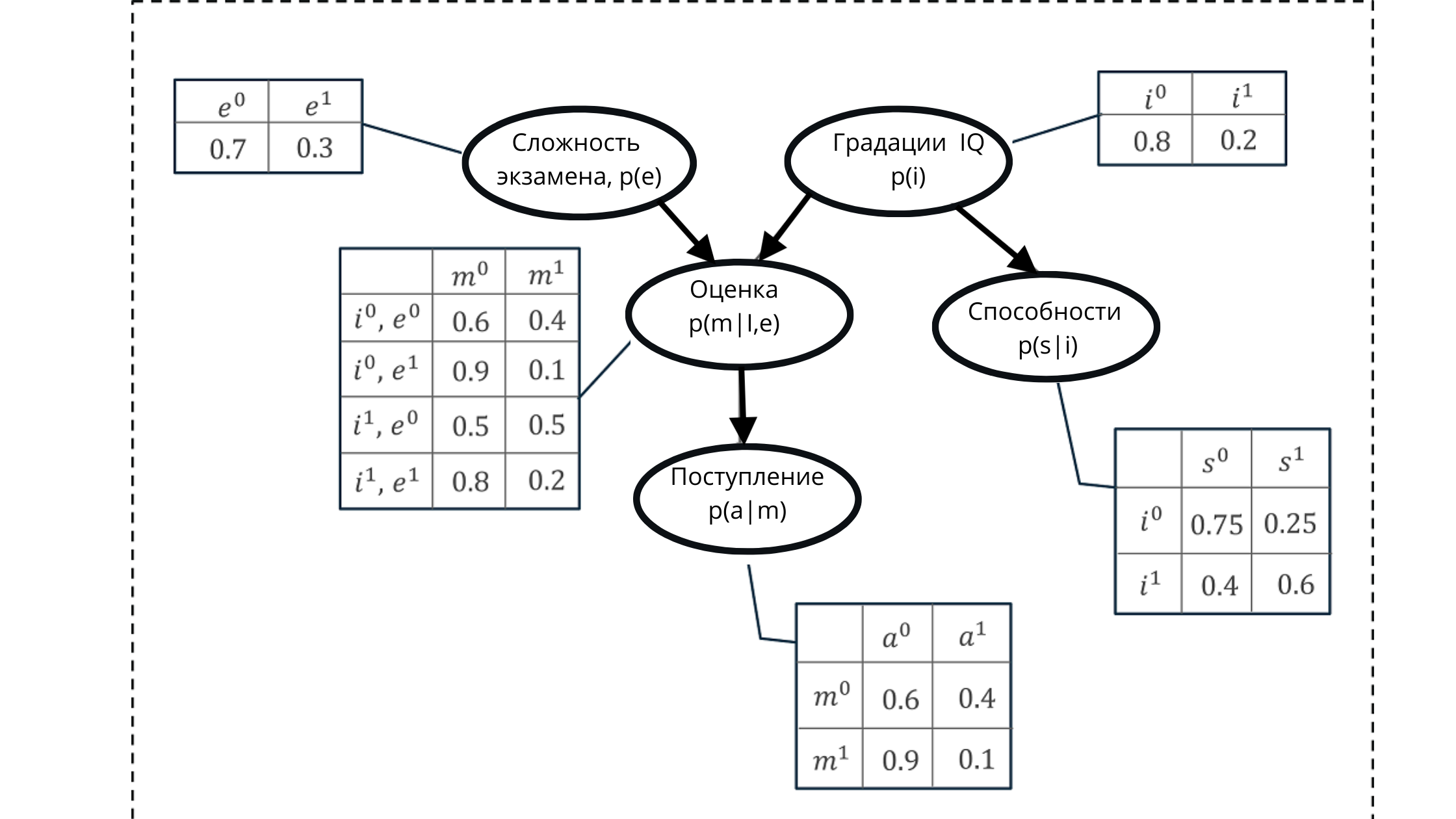
p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e) p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e)

$p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)$

In der Abbildung:

p (e) ist die Wahrscheinlichkeitsverteilung für die Noten der Prüfungsvariablen (beeinflusst die Note p (m | i, e)))

p (i) ist die Wahrscheinlichkeitsverteilung für die Noten der IQ-Variablen (beeinflusst die Note p (m | i, e) )))

p (m | i, e) - Wahrscheinlichkeitsverteilung für Klassenstufen basierend auf IQ-Niveau und Prüfungsschwierigkeiten (abhängig von p (i) und p (e))

p (s | i) - Wahrscheinlichkeitskoeffizienten für die Fähigkeiten der Schüler , basierend auf der Höhe seines IQ (abhängig von der Variablen IQ p (i))

p (a | m) ist die Wahrscheinlichkeit der Einschreibung eines Studenten an der Universität, basierend auf seinen Schätzungen p (m | i, e)

Hier möchte ich Sie daran erinnern, dass die Eigenschaft eines azyklischen Graphen eine Reflexion ist Beziehung. In der Abbildung können wir deutlich sehen, wie sich Elternknoten auf Kinder auswirken und wie Kinder von Eltern abhängen.

Daher ergibt sich die Formulierung des Wertesatzes, der unter Verwendung von Bayes'schen Netzwerken erzeugt wird.

Die Essenz des Bayesianischen Netzwerks

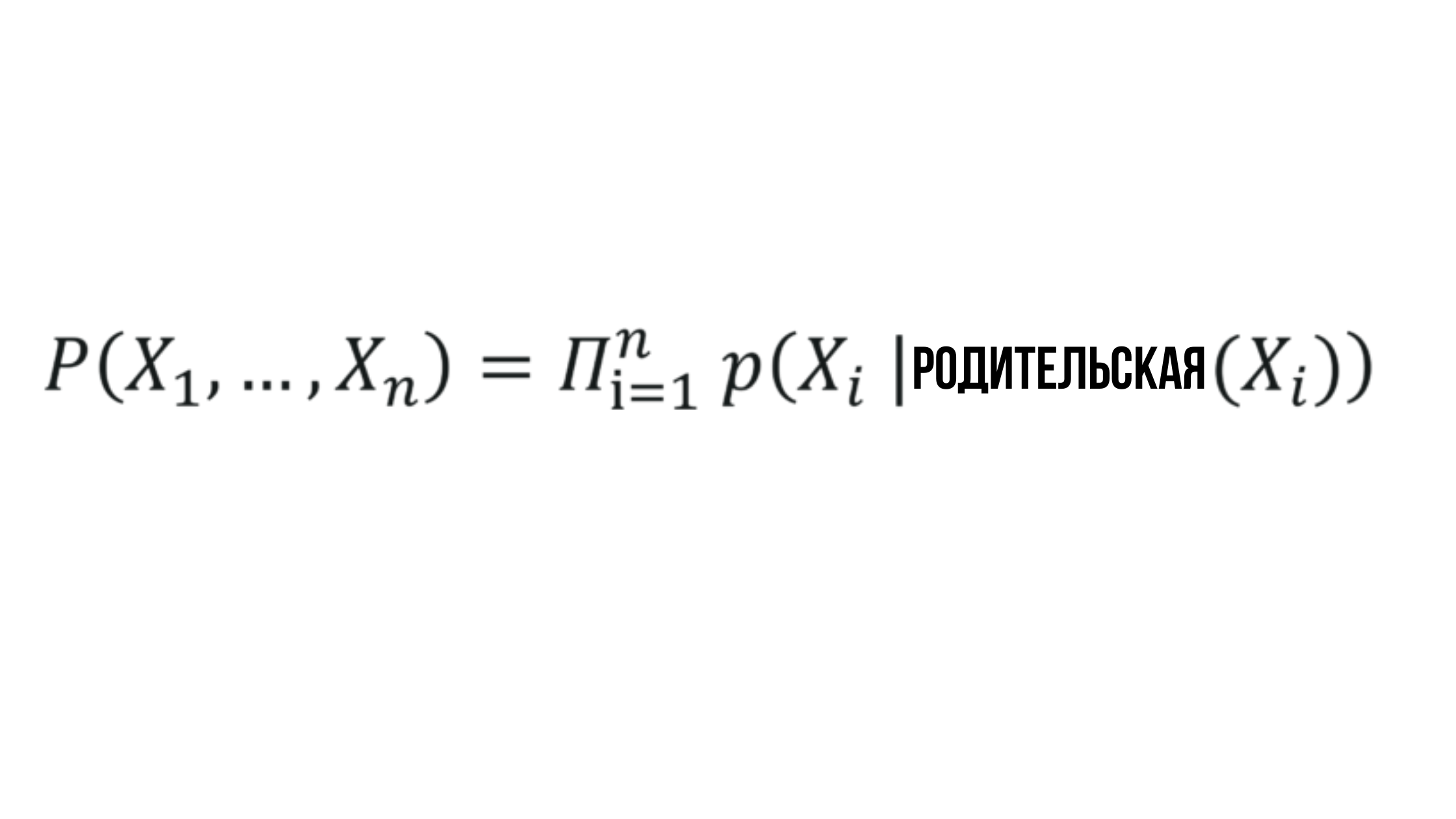
Wobei die Wahrscheinlichkeit X_i von der Wahrscheinlichkeit des entsprechenden Elternknotens abhängt und durch einen beliebigen Zufallswert dargestellt werden kann.

Klingt einfach und zu Recht - Bayesianische Netzwerke sind eine der einfachsten Methoden für deskriptive Analysen, Vorhersagemodelle und mehr.

Bayesianisches Netzwerk in Python

Schauen wir uns an, wie wir ein Bayes'sches Netzwerk auf ein Problem anwenden, das als Monty Hall-Paradoxon bezeichnet wird.

Fazit: Stellen Sie sich vor, Sie sind Teilnehmer am Update-Format des Spiels "Field of Miracles". Die Trommel dreht sich nicht mehr - jetzt sollten Sie Ihr F nicht mehr anwenden, sondern mit p spielen.

Vor Ihnen befinden sich drei Türen, hinter denen sich wahrscheinlich ein Auto befindet. Die Türen, hinter denen sich kein Auto befindet, führen Sie zu den Ziegen.

Nach der Auswahl öffnet der Anführer der verbleibenden Person diejenige, die zur Ziege führt (z. B. haben Sie Tür 1 gewählt, was bedeutet, dass der Anführer entweder Tür 2 oder 3 öffnet) und fordert Sie auf, Ihre Auswahl zu ändern.

Frage: Was tun?

Lösung: Zunächst beträgt die Wahrscheinlichkeit, eine Tür mit einem Auto zu wählen, 33% und mit einer Ziege 66%.

Wenn Sie 33% erreichen, führt ein Türwechsel zu einem Verlust => Gewinnchance == 33%
Wenn Sie 66% erreichen, führt die Änderung zu einem Gewinn => Gewinnwahrscheinlichkeit == 66%

Aus mathematischer Sicht führt das Ändern der Tür insgesamt zu einem Gewinn von 66% und zu einem Verlust von 33%. Daher besteht die richtige Strategie darin, die Tür zu wechseln.

Wir sprechen hier jedoch über das Netzwerk, und es kann viele Türen geben, sodass wir die Lösung auf das Modell übertragen werden.

Lassen Sie uns einen gerichteten azyklischen Graphen mit drei Knoten konstruieren:

Preistür (immer mit dem Auto)
Wählbare Tür (entweder mit einem Auto oder mit einer Ziege)
Öffnungsfähige Tür in Event 1 (immer mit einer Ziege)

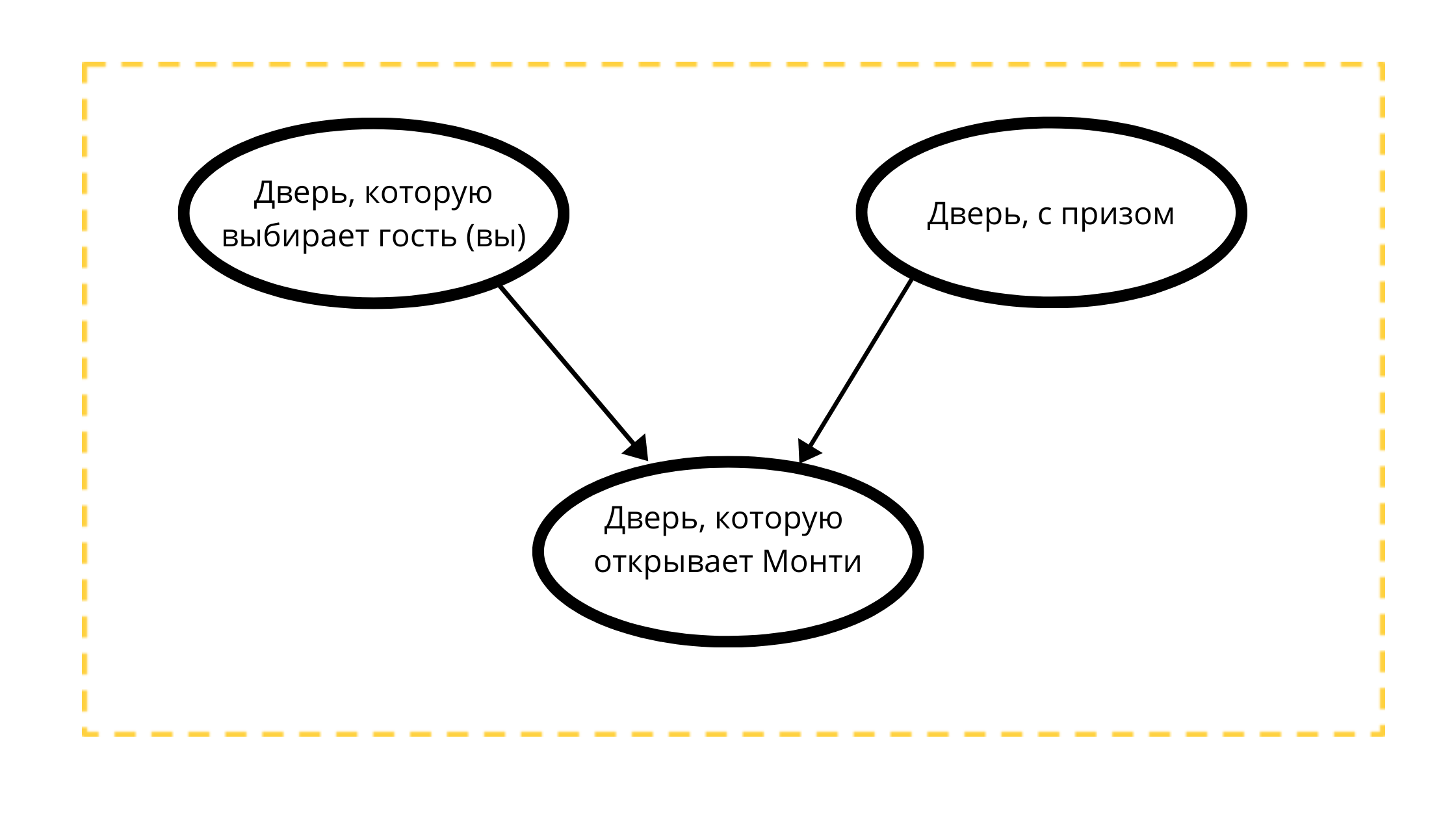
Lesen des Grafen:

Die Tür, die Monty öffnen wird, wird streng von zwei Variablen beeinflusst:

Die vom Gast (Ihnen) tk Monti 100% gewählte Tür öffnet Ihre Wahl NICHT
Eine Tür mit einem Preis, vielleicht öffnet Monty immer eine Tür ohne Preis.

Gemäß den mathematischen Bedingungen des klassischen Beispiels kann sich der Preis mit gleicher Wahrscheinlichkeit hinter einer der Türen befinden, genauso wie Sie mit gleicher Wahrscheinlichkeit eine Tür auswählen können.

#   
import math
from pomegranate import *
 
#    "  " (   3)
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#    "   " (    )
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#  ,       ,     
#    
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
 
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
 
#  
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()

Im Snippet sind die Werte:

A - die vom Gast gewählte Tür
B - Preistür
C - Tür von Monty gewählt

Auf dem Fragment berechnen wir den Wahrscheinlichkeitswert für jeden der Knoten des Graphen. Die beiden oberen Knoten gehorchen in unserem Beispiel einer gleichen Wahrscheinlichkeitsverteilung, und der dritte spiegelt die abhängige Verteilung wider. Um nicht an Wert zu verlieren, werden daher die Wahrscheinlichkeiten jeder der möglichen Kombinationen des Spiels für berechnet.

Nachdem wir die Daten vorbereitet haben, erstellen wir ein Bayes'sches Netzwerk.

Hierbei ist zu beachten, dass eine der Eigenschaften eines solchen Netzwerks darin besteht, den Einfluss versteckter Variablen auf Observable aufzudecken. Gleichzeitig müssen weder versteckte noch beobachtbare Variablen im Voraus spezifiziert oder bestimmt werden - das Modell selbst untersucht den Einfluss versteckter Variablen und wird dies umso genauer tun, je mehr Variablen es empfängt.

Beginnen wir mit Vorhersagen.

beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
 
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}

Lassen Sie uns das Fragment am Beispiel der Variablen A analysieren.

Angenommen, der Gast hat es ausgewählt (A).

Das Ereignis „Es gibt einen Preis hinter der Tür“ in der Phase der Auswahl einer Tür durch einen Gast hat eine Wahrscheinlichkeitsverteilung == ⅓ (da jede Tür gleich wahrscheinlich ein Preis sein kann).

Addieren Sie als Nächstes den Wert der Wahrscheinlichkeiten, dass die Tür der Preis ist, wenn die Tür von Monty ausgewählt wird. Da wir in Schritt 1 nicht wissen, ob die Preistür durch unsere eigene (Gast-) Wahl ausgeschlossen wurde, beträgt die Wahrscheinlichkeit, dass die Tür zu diesem Zeitpunkt ein Preis ist, 50/50

beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B

In diesem Schritt ändern wir die Eingabewerte für unser Netzwerk. Jetzt funktioniert es mit der Wahrscheinlichkeitsverteilung, die in den Schritten 1 und 2 erhalten wurde, wobei

Die Gewinnchancen an der Tür unserer Wahl haben sich nicht geändert (33%).
Die Gewinnchancen an der von Monty (B) geöffneten Tür wurden gestrichen
Die Chancen, ein Preisgeld an der Tür zu sein, das ignoriert wurde, nahmen einen Wert von 66% an

Wie oben festgestellt wurde, besteht die richtige Strategie der Gäste für dieses Spiel darin, die Tür zu wechseln - diejenigen, die die Tür mathematisch ändern, haben ⅔ Gewinnchancen gegen diejenigen, die die Tür nicht ändern (⅓).

In dem Beispiel mit drei Knoten sind zweifellos manuelle Berechnungen ausreichend, aber mit einer Zunahme der Anzahl von Variablen, Knoten und Einflussfaktoren kann das Bayes'sche Netzwerk das Problem des Vorhersagewerts lösen.

Anwendung von Bayes'schen Netzwerken

1. Diagnose:

symptombasierte Vorhersage von Krankheiten
Symptommodellierung für die Grunderkrankung

2. Durchsuchen des Internets:

Bildung von Suchergebnissen basierend auf der Analyse des Benutzerkontexts (Absichten)

3. Klassifizierung von Dokumenten:

Spamfilter basierend auf Kontextanalyse
Verteilung der Dokumentation nach Kategorie / Klasse

4. Gentechnik

Modellierung des Verhaltens von Genregulationsnetzwerken basierend auf den Verbindungen und Beziehungen von DNA-Segmenten

5. Arzneimittel:

Überwachung und prädiktiver Wert akzeptabler Dosen

Die obigen Beispiele sind Fakten. Für ein vollständiges Verständnis ist es wichtig, sich vorzustellen, in welchem Stadium die Erstellung eines Bayes'schen Netzwerks verbunden ist und aus welchen Knoten das Diagramm besteht, aus dem es besteht.

Das Problem des Monty Hall-Paradoxons ist nur eine Grundlage, die es ermöglicht, die Funktionsweise von Ketten anhand einer Kombination aus abhängigen und unabhängigen Wahrscheinlichkeitsverteilungen mit den Fingerspitzen zu veranschaulichen. Ich hoffe ich habe es verstanden.

PS Ich bin kein Python-Ass und lerne nur, daher kann ich nicht für den Code des Autors verantwortlich sein. Mit der Veröffentlichung dieses Artikels über Habré wird die intellektuelle Arbeit der Übersetzung stärker in die Welt entlassen. Ich denke, dass ich in Zukunft meine eigenen Tutorials erstellen kann - in ihnen werde ich mich bereits über konstruktive Gedanken zum Code freuen.

Bayesianische Netzwerke mit Python - was und warum?