Das mathematische Modell des Phänomens postuliert, dass alle Prozesse in einer 4-dimensionalen Raumzeit stattfinden, in der sich die SRT-Phänomene aus der Beibehaltung des Ereignisintervalls während der Transformation der Rotation des Koordinatensystems ergeben. Es ist kaum zu leugnen, dass sich die Realität sozusagen über mathematische Konstruktionen erstreckt. Darüber hinaus beeinträchtigt die Tatsache, dass imaginäre Zahlen in Wirklichkeit eine unvorstellbare Rolle spielen, den Erfolg der Wissenschaft nicht. Sogar E. Mach sagte, dass Erklärungen überflüssig sind, wenn die beobachteten Phänomene durch Formeln gut beschrieben werden. Und lassen Sie uns nicht mit dieser empirischen Kritik streiten.
Mathematiker erfinden Abstraktionen und probieren sie in die Realität um. Daher die Singularität, Wurmlöcher und andere exotische Dinge. Oder vielleicht lohnt es sich , sich zum Beispiel vorzustellen , was sich in unseren Vorstellungen von der Welt ändern würde, wenn die Ursache für die Lorentz-Kontraktion ein hypothetisch angenommener physikalischer Mechanismus wäre. Warum nicht?
1 die physikalische Ursache der Lorentz-Kontraktion
Zunächst möchte ich die scheinbar offensichtliche Maxime ausdrücken, dass Teilchen, Atome und Moleküle über physikalische Felder miteinander interagieren . Wir können natürlich sagen, dass sie Quantenteilchen austauschen, aber wir spielen jetzt auf dem Gebiet der relativistischen Theorie, also werden wir vorerst die Quanten vergessen. Die erste fantastische Annahme ist also, dass gerade aufgrund des gegenseitigen Ausgleichs von Feldeffekten die Partikel einer bestimmten Konfiguration hinzugefügt werden und Körper bilden . Wenn ein Teilchen von der Gleichgewichtsposition abweicht, läuft eine Feldstörung davon ab, die den Rest der Teilchen bewegt, was wiederum einen umgekehrten Feldeffekt von ihnen auf dieses Teilchen verursacht.
Und die zweite Annahme ist dieFeldstörung breitet sich in einem bestimmten gemeinsamen Raum mit einer bestimmten bestimmten Geschwindigkeit aus . Und die fantastische Natur dieser Annahme ist, dass das Feld laut Wissenschaft in der 4-dimensionalen Raumzeit (P-W) für sich existiert und sich über nichts ausbreitet. Im Allgemeinen ist es in der Wissenschaft schwierig ... Wir gehen davon aus, dass sich die Felder in einem einzigen dreidimensionalen Raum ausbreiten und existieren - in dem wir uns befinden, die Erde und die Sterne. Es scheint, dass dies selbstverständlich ist und wer nicht weiß, aber mal sehen, was passiert. Wer sich nicht mit Formeln beschäftigen möchte, kann sich darauf beschränken, nur den ausgewählten Text zu lesen.
Wir sind uns also einig, dass es eine Wechselwirkungszeit zwischen den Partikeln gibt, der sich aus dem Zeitpunkt des Eintreffens der Empörung und dem Zeitpunkt der Rückgabe der Antwort von ihnen zusammensetzt. Infolgedessen wird die vorherige Konfiguration des Körpers schrittweise wieder hergestellt. Abb.1 Feldeinflüsse, die die Position des Partikels bestimmen
Für jeden Punkt des Körpers ist es möglich, Gruppen von Punkten zu unterscheiden, mit denen es gleiche Wechselwirkungszeiten hat und die wir mit diesem Punkt als isochron bezeichnen. Die Situation ist in Abb. 1 dargestellt. Selbstverständlich ruht die Kugel jeden Rest Radius R um einen Punkt ist der Ort der Punkte (GMT) isochrone damit.
Es ist zu beachten, dass die Bewegung eines Teilchens zu jedem Zeitpunkt durch die Summe der resultierenden Kräfte bestimmt wird, die gleichzeitig aus der Gesamtheit aller mit ihm isochronen Teilchengruppen aufgebracht werden... Versuchen wir herauszufinden, wie sich die Oberfläche der GMT, die aus einer Reihe von Punkten 2, 3 usw. besteht, ändert, wenn sich der Körper bewegt. mit den gleichen Wechselwirkungszeiten mit Punkt 1, der möglicherweise keine Kugel mehr ist.
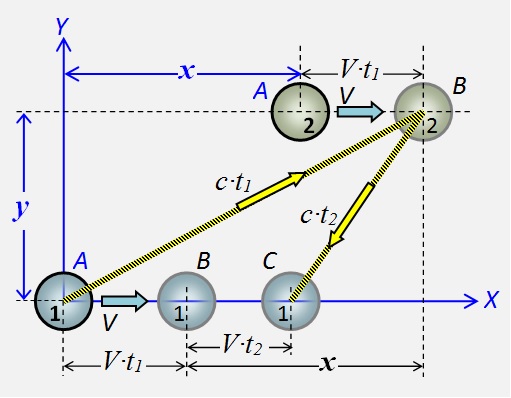Die Körperpunkte 1 und 2 seien gegenseitig fixiert und bewegen sich synchron mit der Geschwindigkeit V nach rechts . Wenn sich ein Punkt am Ursprung befindet, wird das Störfeld an Punkt 2 gesendet. Die gegenseitige Anordnung der mit dem Buchstaben A gekennzeichneten Punkte . Abb.2 Schema der Feldwechselwirkungen von Körperpunkten - hin und her
Wenn die Störung Punkt 2 erreicht, legt sie die Strecke V ∙ t 1 zurück . Positionen markierten Punkte mit dem Buchstaben B . Während der Zeit, in der die Störung von Punkt 2 zu Punkt 1 zurückkehrt, legt Punkt 2 die Entfernung zurückV ∙ t 2 . Ihre neue Position ist mit dem C gekennzeichnet .
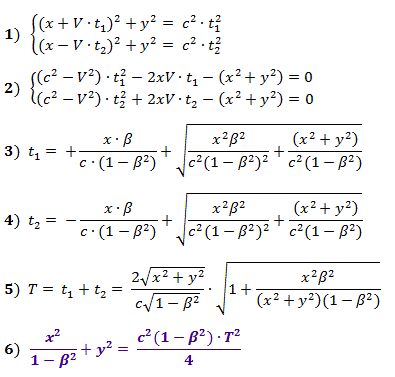Die Formeln (1) beschreiben gemäß dem Satz von Pythagoras die Abstände in Fig. 2, und die daraus erhaltenen (2) sind Gleichungen zur Berechnung der Zeiten t 1 und t 2 , deren Werte durch die Formeln (3) und (4) für positive Werte der Wurzeln gegeben sind, wobei β = V / c .
Die Formel (5) gibt den Wert der Interaktionszeit vom Senden einer Störung bis zum Empfangen einer Antwort an.
Aus (5) erhalten wir Gleichung (6) für die Koordinaten x und y des geometrischen Ortes isochroner Punkte, mit denen die Wechselwirkungszeit von Punkt 1 gleich ist.
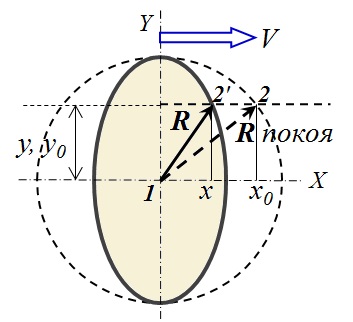Die Formel (6) beschreibt das in Fig. 3 gezeigte Ellipsoid, das entlang der Bewegungsrichtung (entlang der X-Achse) um das √ (1 - β 2 ) -fache komprimiert ist, dh gemäß der Lorentz-Formel. Punkt 2 auf der Oberfläche der Kugel in Ruhe bewegt sich während der Bewegung zu Position 2 ' . In diesem Fall bleiben Materialpunkte, die mit Punkt 1 in Ruhe isochron waren, während der Bewegung isochron . Abb.3
also bei Bewegung, wird ein materielles Objekt komprimiert nach Lorentz gerade weil das sehr „Bild“ physikalischer Felder zusammengedrückt wird, die gewährleistet , seine Integrität im Raum .
Da die Lorentz-Kontraktion für alle isochronen Punkte, die jeden Punkt des Objekts umgeben, gleich ist, zieht sich das gesamte sich bewegende Objekt entlang der Bewegungsachse gleichmäßig proportional zusammen.
2. Ableitung der Formel für die Zeitdilatation
Bestimmen wir die Interaktionszeit, wenn sich das Objekt bewegt, im Vergleich zur Interaktionszeit in Ruhe.
Die Formeln (7) beziehen die Koordinaten der Punkte während der Bewegung mit ihren ruhenden Koordinaten gemäß
Gleichung (6). Die Formel (8) berechnet die Interaktionszeit in Ruhe. Die Formeln (9) und (10) wurden aus der Formel (6) erhalten, indem die Werte der Koordinaten x und y und R der Ruhe aus den Formeln (7) eingesetzt wurden. Formel (11) entspricht (10). Die Formel (12), die aus (11) durch Einsetzen der linken Seite der Formel (8) erhalten wird, verbindet die Wechselwirkungszeiten in Ruhe und während der Bewegung. In der traditionellen Form spiegelt sich dies in Formel (13) wider, wobei T 0 das Zeitintervall zwischen Ereignissen in einem ruhenden Objekt ist undT ist das Zeitintervall zwischen denselben Ereignissen in einem sich bewegenden Körper.
So erhöhen sich die Interaktionszeiten aller Punkte in einem sich bewegenden Objekt nach Lorentz im gleichen Verhältnis wie die Interaktionszeit in Ruhe. Dementsprechend verlangsamen sich im Allgemeinen alle Prozesse in einem sich bewegenden Objekt tatsächlich in derselben Hinsicht .
Der Grund für die Verlangsamung der Zeit ist leicht zu verstehen, wenn wir berücksichtigen, dass die Feldstörung von der Rückseite der wechselwirkenden Teilchen die vordere in Bewegungsrichtung einholen muss . Wenn die Geschwindigkeit des Körpers fast der Lichtgeschwindigkeit entspricht, dauert das Aufholen lange, und wenn die Geschwindigkeit des Körpers der Lichtgeschwindigkeit entspricht, holt er sie niemals ein. Alle Veränderungen im Körper werden aufhören und die Zeit in ihm scheint anzuhalten.
3. Erklärung des Phänomens der Konstanz der Lichtgeschwindigkeit usw.
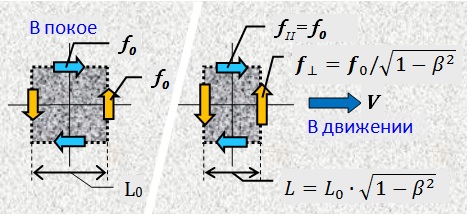
Lassen Sie uns ein Gedankenexperiment machen. Lassen Sie einen Lichtimpuls vom letzten Wagen des Zuges ausgehen, der in seinem Hauptwagen empfangen wird. Wir müssen die Zeit T 0 messen, die das Licht für den Durchgang eines Zuges bekannter Länge L 0 in seinem eigenen System benötigt. Im Beweis werden wir die Annahmen über die Homogenität und Isotropie des Raums verwenden, insbesondere werden wir die gleichen Messergebnisse für die erste und zweite Hälfte des Zuges sowie für die Vorwärts- und Rückwärtsrichtung annehmen. Genau genommen gelten diese Annahmen jedoch nur innerhalb des Ortes und der Zeit des Experiments.
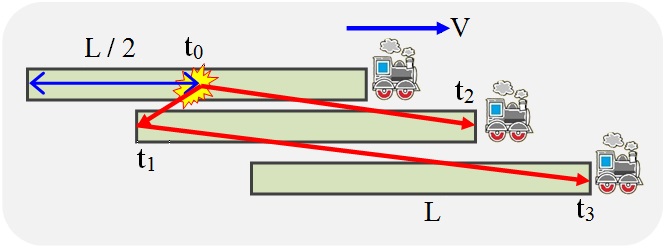
Abb. 4. Gedankenexperiment zur Bestimmung der Lichtgeschwindigkeit in einem fahrenden Zug
Um den Moment des Sendens eines Signals vom letzten Wagen des Zuges und den Start des Zeitzählers in seinem vorderen Wagen zu synchronisieren, verwenden wir einen Startlichtimpuls von der Mitte des Zuges zu beiden Enden.
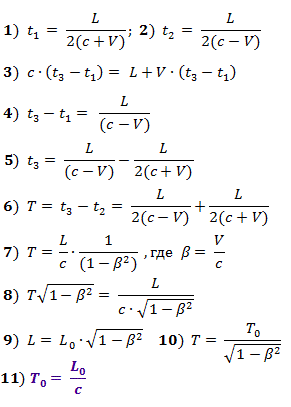
Wenn das Startsignal aus der Mitte des Zuges sein Heck erreicht (Zeit t 1 ), wird ein Lichtimpuls gesendet. Wenn das Startsignal den Kopf des Zuges erreicht (Zeit t 2 ), beginnt der Countdown bis zum Eintreffen des gesendeten Impulses.
Wenn sich Licht zum Heck bewegt, wird seine Geschwindigkeit zur Geschwindigkeit des Zuges addiert, während zum Kopf die Geschwindigkeit des Zuges abgezogen wird. Wir erhalten die unten angegebenen Beziehungen in den Formeln (1) - (6).
Zeit T = t 3 - t 2 ist das Zeitintervall, das,Nach Angaben des Beobachters im Zug werden die Ereignisse des Zeitpunkts des Sendens des Signals vom Ende des Zuges (ab dem Zeitpunkt des Empfangs des Startsignals dort) und des Zeitpunkts seines Empfangs im Kopf des Zuges getrennt.
Aus (6) erhalten wir die Formel (7), die wir in die Form (8) umwandeln. Ferner werden wir berücksichtigen, dass alle Größen L , T und t hier im Referenzrahmen eines externen Beobachters in dem Raum gemessen werden, in dem das Gedankenexperiment stattfindet. Wenn sich ein Objekt im Raum bewegt , erfährt seine Länge, wie in Kapitel 1 bewiesen , tatsächlich eine Lorentz-Kontraktion und die Zeiten der Ereignisse, wie in Kapitel 2 bewiesentatsächlich um die gleiche Anzahl von Malen verlangsamen, d.h. Fahren Sie länger fort als in Ruhe, was sich in den Formeln (9) und (10) widerspiegelt. Wenn wir diese Verhältnisse in die Formel (8) für das Intervall T - die Laufzeit des Lichts vom Heck zum Kopf des Zuges - einsetzen, erhalten wir die Beziehung (11).
Aber in welchem Verhältnis stehen diese T 0 und L 0 in Ruhe zu ihrer eigenen Zeit und Länge für dieselben Ereignisse, gemessen im Trägheitsrahmen (IRF) eines fahrenden Zuges? Offensichtlich sind sie gleich . Tatsache ist, dass Zeit und Länge durch ihre Beziehung zu Standards numerisch ausgedrückt werden. Dementsprechend werden Messungen der zeitlichen und räumlichen Koordinaten von etwas, das in Ruhe gemacht wird, numerisch seinsind gleich den Messungen derselben, die in einer sich bewegenden ISO durchgeführt werden, da sich beim Verschieben die Werte sowohl der Messungen als auch der Standards proportional ändern.
Die Frage ist, wie genau sie sich ändern, wenn sie sich im Raum bewegen. Ein Gedankenexperiment mit einem Zug beweist, dass sie sich so ändern, dass der im IFR gemessene numerische Wert der Lichtgeschwindigkeit gleich dem Wert seiner Raumgeschwindigkeit bleibt . Genau dies war nicht a priori offensichtlich und erforderte einen Beweis.
Wir sehen, dass das "Postulat der Konstanz der Lichtgeschwindigkeit" allein aus der Tatsache der Lorentz-Kontraktion abgeleitet wird, die mathematisch aus der Abhängigkeit des Ortes der materiellen Materie von der Ausbreitungsgeschwindigkeit und der Konfiguration physikalischer Felder im Raum abgeleitet wird .
Um das Bild zu vervollständigen, definieren wir auch die Lichtgeschwindigkeit über die Bewegung des Zuges, beispielsweise zwischen den Wänden des Wagens in einem Abstand S 0 voneinander. Dazu messen wir die Bewegungszeit des Lichtimpulses ( 2 · t 0 ) hin und her. Angesichts der offensichtlichen Symmetrie von "dort" und "zurück" werden wir nur "dort" betrachten. In dem System eines äußeren Beobachters tritt eine Bewegung im Raum auf, wie in Fig. 5 gezeigt.
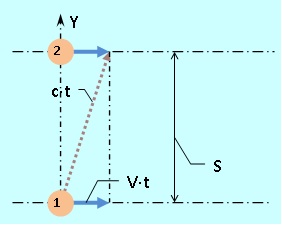Wir haben also (c · t) 2 = S 2 + (V · t) 2 , woraus wir t = S / (c · √ (1 - β²)) erhalten , wobei β = V / c .
Im Zugsystem ist die verstrichene Eigenzeit t 0verbunden mit der im Raum verstrichenen Zeit durch die Beziehung t = t 0 / (√ (1 - β²)) . Wenn wir diesen Ausdruck in die Formel für t im Raum einsetzen, erhalten wir t 0 = S / c .
Abb. 5. Gedankenexperiment zur Bestimmung der Lichtgeschwindigkeit in einem fahrenden Zug /
Im eigenen System des Zuges für dasselbe t 0 haben wir die Beziehung t 0 = S 0 / c 0 . Da sich die Querabmessungen jedoch während der Bewegung nicht ändern, d.h. S = S 0 , wir erhalten c 0 = c .
Ich nehme an, es besteht keine Notwendigkeit, die Konstanz der gemessenen Lichtgeschwindigkeit für eine beliebige Ausrichtung des Strahls zu beweisen, was nur zu unnötiger Komplexität führen würde. In Anbetracht der nachgewiesenen Invarianz der Lichtgeschwindigkeit ist es einfach, die Lorentz-Transformationen (L) abzuleiten, ohne die Maxwell-Gleichungen oder den mathematisch abstrakten Minkowski-Raum zu berücksichtigen.
4. Ableitung von Lorentz-Transformationen
Das Ereignis besteht in der Ankunft eines Lichtimpulses am Punkt " E ", der
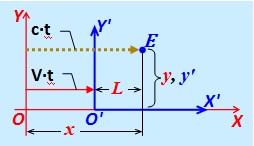sich in unveränderten Koordinaten x ' und y' im Referenzsystem {X ', Y'} befindet und sich mit einer Geschwindigkeit V relativ zum festen IFR {X, Y} bewegt , die zu dem Zeitpunkt gesendet wird, als Die Punkte O und O 'beider COs stimmten überein. Abb. 6.
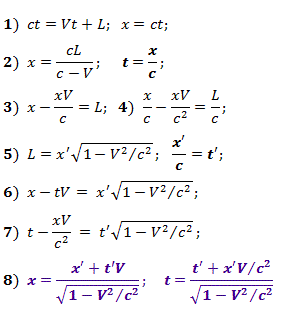In seiner eigenen CO {X ', Y'} Länge L , gemessen in CO {X, Y}, entspricht die x'- Koordinate . Für das Ereignis ist das Gleichungssystem (1) gültig, dessen Lösung wir erhalten (2) und dann (3) und (4).
Da die Längen der bewegten Körper nach Lorentz komprimiert sind und die Lichtgeschwindigkeit, wie in Kapitel 3 bewiesen , in jedem FR gleich ist, gilt für das richtige x 'undt ' in {X', Y '} Beziehungen (5) sind gültig. Wenn wir die Beziehungen von (5) in (3) einsetzen, erhalten wir (6), und wenn wir sie in (4) einsetzen, erhalten wir (7). Aufgrund der Relativität der Bewegung können wir das sich bewegende System {X, Y} betrachten, aber dann ist es in (6) und (7) notwendig, die nicht schattierten Variablen durch die schattierten zu ersetzen, und die Geschwindigkeit V sollte mit dem entgegengesetzten Vorzeichen genommen werden, oder einfach das System in Bezug auf x und t lösen.
Als Ergebnis erhalten wir Ausdrücke (8) für die kanonische Form von Lorentz-Transformationen von Koordinaten und Zeit von Ereignissen in verschiedenen IFRs.
Bei Verwendung von PL als rein formale mathematische Methode bleibt der physikalische Mechanismus von SRT-Phänomenen unmanifestiert. Daher wurde in meinen vorherigen Artikeln über den relativistischen Doppler-Effekt undLichtaberrationen sowie die Reflexionsgesetze eines sich bewegenden Schrägspiegels wurden im Prinzip nicht verwendet, um die physikalischen Ursachen dieser Phänomene zu demonstrieren.
5. Begründung des Relativitätsprinzips und Einschränkungen seiner Anwendbarkeit
Es ist zu beachten, dass, wenn in dem Diagramm in Fig. 1 die Störung von Punkt 1 zur GMT von Punkten, die damit isochron sind, in Ruhe gleichzeitig auftrat, dies während der Bewegung in dem Diagramm in Fig. 2 nicht mehr erfüllt ist. An jedem Punkt dieser GMT wird die Reaktion auf die Störung zu unterschiedlichen Zeiten erzeugt, aber sie konvergieren gleichzeitig an Punkt 1 . Die Frage ist, wird das Ergebnis das gleiche sein wie in Ruhe?
Es wurde oben bewiesen, dass in jedem IFR die gemessenen richtigen Zeiten und Abstände zwischen allen Punkten dieselben sind wie in Ruhe . Folglich wird beispielsweise die Anzahl der Perioden eingeleitetDie elektromagnetische Welle zwischen beliebigen Punkten ist dieselbe wie in Ruhe. Da die Störung eines Feldes einer beliebigen Konfiguration durch eine Erweiterung in einer Reihe monochromatischer Harmonischer dargestellt werden kann, sind die Konfigurationen und Intensitäten aller Felder im intrinsischen System in Ruhe jeweils gleich. Folglich werden die Phasenbeziehungen und die Synchronisation der Felder, die den Körper bilden, nicht verletzt, und alle Prozesse in ihm verlaufen wie im Ruhezustand.
Dies ist genau das, was Einsteins "Relativitätsprinzip" verkündet, und wie wir sehen, wird es mathematisch unweigerlich aus zwei Annahmen abgeleitet (siehe Kapitel 1). Lassen Sie mich daran erinnern: Erstens, dass die Position realer Teilchen durch die Struktur der Felder bestimmt wird , und zweitens , dassFeldausbreitung erfolgt mit endlicher Geschwindigkeit .
Das heißt, das Relativitätsprinzip ist sozusagen nicht a priori ein universelles Prinzip , sondern eine Konsequenz und hat klare Grenzen der Anwendbarkeit . Insbesondere hat die Lichtgeschwindigkeit nicht die Bedeutung einer Weltkonstante, sondern ist eine bestimmte Lichtgeschwindigkeit in einem bestimmten Raumbereich . Und an einigen Stellen kann es aufgrund der Wechselwirkung mit lokalen physikalischen Feldern, beispielsweise der Schwerkraft, anders sein. Wir haben also zwei Alternativen, die genau die gleichen relativistischen Formeln ergeben:
- das erste, orthodox und wissenschaftlich: erfordert die Postulierung eines a priori wahren Relativitätsprinzips ;
- : ,
Im ersten Fall müssen die Phänomene der SRT nicht erklärt werden, und ihre Ursachen und Mechanismen bleiben unbekannt. Die Frage "Warum?" es stellt sich sogar heraus, dass es außerhalb der Wissenschaft liegt.
Im zweiten Fall sind die Annahmen sogar ziemlich logisch und es ist nichts erforderlich, um sie zu postulieren, und sie sind nur insofern „fantastisch“, als andere Gründe für den Relativismus in der Wissenschaft akzeptiert werden. Auf die Frage "Warum sind die SRT-Phänomene so?" hier wird eine klare und sogar fast triviale Erklärung gegeben. Es ist jedoch dringend erforderlich, die Natur der Materie und ihre Beziehung zu physischen Feldern herauszufinden.
Deshalb werden wir weiter phantasieren.
6. Herleitung der Formel E = Mc² und der Dynamikgleichungen
Lassen Sie uns zunächst herausfinden, wie sich die Kräfte mit relativistischen Geschwindigkeiten umwandeln. Wählen wir das Volumenelement im Körper aus, auf das die ausgeglichenen Kräfte wirken. Wenn sich der Körper bewegt, nimmt die Längsgröße (entlang der Bewegungsbahn) des ausgewählten Elements
entsprechend dem Lorentz-Koeffizienten ab. Damit das Element im Gleichgewicht bleibt, müssen die Kräfte senkrecht zur Bewegung in genau demselben Verhältnis zunehmen. Abb. 7.
Die Größe der Kräfte parallel zur Bewegung ändert sich nicht. Der Faktor der Abhängigkeit der Kräfte von der Orientierung relativ zur Bewegungsrichtung sollte bei der Vektorexpansion der Kräfte in den folgenden Formeln berücksichtigt werden.
Es ist zu beachten, dass die Beschleunigung des Körpers auf eine bestimmte Geschwindigkeit durch die ausgeübte Kraft ausgeführt wird, die dementsprechend einige Arbeit leistet, wodurch die Energie des Körpers erhöht wird. UNDWas ist der Unterschied zwischen einem zerstreuten Körper im Raum und einem Körper in Ruhe? Die Tatsache, dass das Übertaktete nach Lorentz komprimiert ist . In Kapitel 1 wird eine Formel für den Ort von Punkten (GMT) abgeleitet, die einen bestimmten Punkt umgeben, von dem aus sie dieselbe Interaktionszeit von physikalischen Feldern haben. Diese GMT stellt sich als nach Lorentz in Bewegungsrichtung komprimiertes Ellipsoid heraus. Achten wir nun darauf, dass das Volumen W dieses Ellipsoids proportional zur Lorentz-Kontraktion abnimmt. Dies spiegelt sich in der folgenden Formel (1) wider. Nehmen wir nun eine wirklich fantastische Annahme an, dass beim Beschleunigen eines Körpers die Kraftarbeit darauf verwendet wird, das Raumvolumen zu komprimieren, das er einnimmt, die dann in der Freizügigkeit unverändert bleibt. Zumindest ist diese Annahme nicht schlechter als die wissenschaftliche Maxime, dass sich der Raum verbiegen oder anschwellen kann.
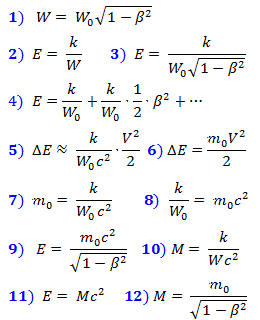Angenommen, diese Energie E ist umgekehrt proportional zu dem Volumen, auf das sie nach Formel (2) oder (3) nach Einsetzen von (1) komprimiert werden konnte.
Wir erweitern E von (3) in eine Taylor-Reihe (4), wobei (5) das Energieinkrement von der Geschwindigkeit in erster Näherung bei niedrigen Geschwindigkeiten ist. Bei niedrigen Geschwindigkeiten ist es aber auch gleich (6). Wenn wir (5) und (6) vergleichen, erhalten wir (7) und (8). Wenn wir (8) durch (3) ersetzen, erhalten wir (9), das die Energie eines Körpers im komprimierten Raum mit seiner Ruhemasse verbindet.
Drücken wir die relativistische Masse durch die Formel (10) aus, aus der wir durch Ersetzen von (2) den bekannten Ausdruck (11) erhalten, der Masse und Energie in Beziehung setzt. Wenn wir (9) und (11) vergleichen, erhalten wir (12).
Masse ist nur eine weitere Formulierung der Energie, die beim Komprimieren des Raums aufgewendet wird. Und in diesem Sinne sind sie gleichwertig. Und die Substanz "markiert" nur den Raumbereich, den der Körper einnimmt.
Änderung der Gesamtenergie E des Systems, d.h. Die Kompressionsenergie des Raums entspricht in voller Übereinstimmung mit der klassischen Newtonschen Mechanik der Arbeit der ausgeübten Kraft als Produkt der Kraft pro Pfad, und die Änderung des Impulses P des Systems entspricht dem Produkt derselben Kraft und der Zeit seiner Wirkung. Diese Abhängigkeiten spiegeln sich in Formeln (13) wider. Nach dem Einsetzen der Ausdrücke für die Energie aus (11) und den Impuls P.Aus Formel (14) erhalten
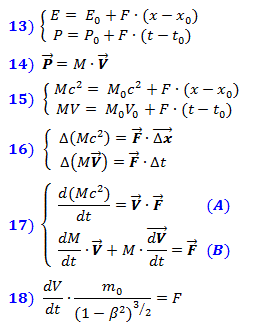wir das Gleichungssystem (15), das in Form von kleinen Inkrementen in (16) in Vektorform geschrieben ist. Dann schreiben wir zeitlich differenzierend das Differentialgleichungssystem (17) auf, das die relativistische Dynamik beschreibt. Die Kraft F muss nicht differenziert werden, da sie extern ist und nicht von den Variationen der Systemvariablen abhängt. Wenn wir den Ausdruck für Masse aus (12) in Formel ( A ) einsetzen, erhalten wir die bekannte relativistische Formel für die geradlinige Bewegung (18). 
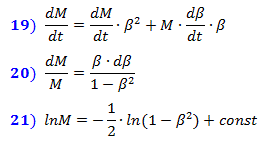Aus dem Gleichungssystem (17) kann die Abhängigkeit der Masse von der Geschwindigkeit ermittelt werden. Einsetzen von F aus Formel ( B ) in Formel ( A ) und Teilen beider Seiten der Gleichheit durch c²Wenn wir entlang der Bewegungsbahn beschleunigen, erhalten wir die Ausdrücke (19) und (20). Woher erhalten wir durch Integration den Ausdruck (21). Es ist leicht zu erkennen, dass es dem logarithmischen Ausdruck (12) für die relativistische Masse entspricht, wobei const gleich dem Logarithmus der Ruhemasse m 0 ist . Dies bedeutet, dass gerade eine solche Abhängigkeit der Masse von der Geschwindigkeit die Entsprechung der Energie Mc² und des Impulses M · V in Formeln (16, 17) sicherstellt . Daraus folgt auch, dass der Wert, den wir zuvor als Ruhemasse angenommen haben, eine von der Geschwindigkeit unabhängige Konstante ist, wie sie in den ursprünglichen Formeln (9) geschrieben steht. Unsere Annahme über die Abhängigkeit der Energie vom Grad der Raumkompression ist also richtig.
Natürlich ist der Anspruch auf Raumkomprimierung nicht sehr überzeugend. Wenn der Raum ein leerer Behälter mit Partikeln und Körpern sein soll, wie kann man dann die Leere komprimieren? Die Leere bleibt die Leere. Die Wissenschaft erlaubt sich jedoch, über die Krümmung des leeren Raums zu sprechen - die Formeln erfordern es. Genau genommen ist sein Raum jedoch eine mathematische Abstraktion.
Aber wir können durchaus davon ausgehen , angemessen , dass der Raum nicht leer, sondern mit einem gewissen Art von Materie gefüllt , die, annehmen, nicht in einem komprimierten Zustand, von uns als Leere wahrgenommen wird... Wenn es zum Beispiel unter Druckspannung steht, haben wir Materialpartikel und Körper. Wenn diese darin ruhen, entspricht der Kompressionsgrad (Energie) eines Abschnitts dieser Materie der Ruhemasse des Körpers, und mit seiner Beschleunigung nehmen sowohl der Kompressionsgrad (Energie) des Körpers als auch die entsprechende Masse zu.
Und in dieser materiellen Umgebung können physikalische Felder, die den Ort und die Wechselwirkung von Partikeln bestimmen (bis zu den "sehr, sehr" primären), die sich, wie wir uns weiterhin vorstellen , als Phänomen der Fokussierung von Feldern aus ihrer Umgebung herausstellen, ohne die sie nicht existieren, durchaus existieren und sich mit einer bestimmten Geschwindigkeit ausbreiten ), deren Ruhe- und Bewegungsenergie durch den Grad der Kompression des von ihnen eingenommenen Bereichs der Primärmaterie bestimmt wird . Tatsächlich,Die Gleichungen der relativistischen Dynamik beschreiben nur die Bewegung dieser Spannungsinhomogenitäten (materiellen Körper) in der Primmaterie . Wie wir sehen konnten, gibt es keine Widersprüche zu Michelsons Experiment und Lorentz-Transformationen.