Joshua Green und Andrew Lobb, gelangweilt in Quarantäne, fanden heraus, wie sie eine der Varianten des Satzes mit rechteckigen Stiften beweisen können

Können alle Arten von Rechtecken in einer geschlossenen Schleife gefunden werden?
Mitte März befanden sich die Mathematiker Joshua Green und Andrew Lobb in einer ähnlichen Position - innerhalb von vier Wänden eingeschlossen, um sich an die wachsende Coronavirus-Epidemie anzupassen. Sie beschlossen, sich damit zu befassen, indem sie sich mit ihren Forschungen befassten.
"Ich denke, die Pandemie war eine Art Katalysator für diesen Prozess", sagte Greene, Professor am Boston College. "Wir haben beschlossen, dass es besser ist, eine gemeinsame Arbeit zu leisten, die uns unterstützen kann."
Eines der Probleme, mit denen sich die beiden Freunde befassten, war eine Variante der geometrischen Frage, die seit über hundert Jahren unbeantwortet blieb.
"Diese Aufgabe ist extrem einfach zu formulieren und zu verstehen, aber sehr schwer zu lösen", sagte erElizabeth Denn aus Washington und der Lee University.
Alles beginnt mit einer geschlossenen Schleife - jedem gekrümmten Pfad, der denselben Anfang und dasselbe Ende hat. Die Aufgabe, die Green und Lobb übernommen haben, besteht im Wesentlichen darin, dass es in einem solchen Pfad Sätze von vier Punkten gibt, die die Eckpunkte eines Rechtecks eines bestimmten Anteils bilden.
Und während dieses "Problem mit rechteckigen Stiften" wie eine Frage klingt, die jeder Schüler mit Lineal und Kompass beantworten kann, widersetzt er sich seit Jahrzehnten den hartnäckigsten Versuchen von Mathematikern. Und als Green und Lobb übernahmen, hatten sie keinen Grund, etwas anderes zu erwarten.
Greene sagte, dass von allen schwierigen Projekten, an denen er arbeitete, "dieses meiner Meinung nach das am wenigsten vielversprechende war".
Aber die Pandemie wuchs, und Green und Lobb, die an der Durham University in England und am Okinawa Institute of Science and Technology arbeiten, führten wöchentliche Zoom-Gespräche und brachten schnell mehrere Ideen hervor. Und dann, am 19. Mai, als viele Teile der Welt wieder geöffnet wurden, veröffentlichten sie ihre Entscheidung .
Ihr letzter Beweis, der zeigt, dass tatsächlich Rechtecke gefunden werden können, führt dieses Problem auf eine völlig andere geometrische Ebene. Und da gibt diese hartnäckige Frage sehr leicht nach.
"Es ist ziemlich komisch", sagte Richard Schwartz von der Brown University. "Diese Idee war perfekt für diese Aufgabe."
Rechtecke neu denken
Das Problem der rechteckigen Zapfen hängt eng mit der Frage zusammen, die der deutsche Mathematiker Otto Töplitz 1911 stellte. Er sagte voraus, dass man auf jeder geschlossenen Kurve vier Punkte finden kann, die ein Quadrat ergeben. Diese Frage von ihm über "quadratische Stifte" bleibt offen.
"Dies ist eine alte und frustrierende Aufgabe, die in keiner Weise gehackt werden kann", sagte Green.
Um die Komplexität des Problems zu verstehen, ist es wichtig, die Eigenschaften der Kurven zu kennen, die im Quadratstiftproblem berücksichtigt werden - dies ist auch wichtig für den Beweis von Green und Lobb.
Dieses Paar löste das Problem für geschlossene Kurven, sowohl "kontinuierlich" als auch "glatt". Kontinuität bedeutet keine Pausen. Glätte bedeutet Kontinuität und keine Ecken. Sie zeichnen wahrscheinlich eine glatte, kontinuierliche Kurve, wenn Sie sich mit Papier und Bleistift an Ihren Schreibtisch setzen. Sie sind "einfacher zu bearbeiten", sagte Green.
Glatte kontinuierliche Kurven unterscheiden sich von einfach kontinuierlichen, aber nicht glatten Kurven, wie sie in der Toeplitz-Vermutung von quadratischen Stiften enthalten sind. Eine solche Kurve kann Ecken haben - Punkte, an denen die Kurve plötzlich abweicht und in eine andere Richtung geht. Ein Paradebeispiel für eine Kurve mit vielen Winkeln ist die schneeflockenartige fraktale Koch-Kurve.in der Tat besteht aus einigen Ecken. Die Koch-Schneeflocke und andere ähnliche Kurven können nicht mit algebraischen Methoden analysiert werden, was ihre Untersuchung besonders schwierig macht.
"Einige kontinuierliche [nicht glatte] Kurven sind einfach ekelhaft", sagte Denn.
Dennoch gehört das von Green und Lobb gelöste Problem zu glatten und daher kontinuierlichen Kurven. Und anstatt herauszufinden, ob es auf solchen Kurven immer vier Punkte gibt, die ein Quadrat bilden - für glatte kontinuierliche Kurven wurde dieses Problem 1929 gelöst -, untersuchten sie etwas anderes: ob es auf solchen Kurven immer vier Punkte gibt, die ein Rechteck eines bestimmten bilden Proportionen, d.h. mit jedem Seitenverhältnis. Für ein Quadrat beträgt dieses Verhältnis 1: 1, für hochauflösende Fernsehgeräte 16: 9.

Der erste große Durchbruch im Problem der rechteckigen Stifte wurde Ende der 1970er Jahre von Herbert Vaughn erzielt. Es bot eine neue Sichtweise auf die Geometrie von Rechtecken und mehrere Methoden, die später von anderen Mathematikern verwendet wurden, darunter Green und Lobb.
"Jeder kennt diesen Beweis", sagte Green. "Es ist fast folkloristisch, man lernt über solche Dinge, indem man alles am Esstisch bespricht."
Anstatt sich ein Rechteck als vier verbundene Punkte vorzustellen, stellte sich Vaughn es als zwei Punktepaare in einer Beziehung zueinander vor.

Stellen Sie sich ein Rechteck mit Eckpunkten ABCD vor. Darin ist der Abstand zwischen den Punkten AC (auf der Diagonale) gleich dem Abstand zwischen den Punkten BD (auf der anderen Diagonale). Auch diese Diagonalen schneiden sich genau in der Mitte.
Wenn Sie in einer geschlossenen Schleife nach Rechtecken suchen, können Sie daher nach Punktpaaren suchen, die an den Enden derselben Liniensegmente liegen, die sich in der Mitte schneiden. Um sie zu finden, ist es wichtig, eine systematische Beschreibung zu finden.
Um zu verstehen, was dies bedeutet, beginnen wir mit etwas Einfacherem. Nehmen Sie die Zahlenreihe. Wählen wir zwei Punkte darauf - sagen wir die Zahlen 7 und 8 - und konstruieren Sie sie als einen Punkt auf der numerischen Ebene (7, 8). Wir können auch Punkte erstellen, die aus zwei identischen Zahlen bestehen (7, 7). Betrachten wir nun alle möglichen Zahlenpaare, die in der Zahlenreihe zu finden sind (und es gibt viele davon!). Wenn wir alle Paare solcher Zahlen bilden, füllen wir die gesamte Zahlenebene. Eine andere Möglichkeit, dies auszudrücken, besteht darin, zu sagen, dass die Zahlenebene "parametrisiert", dh alle Zahlenpaare auf der Zahlenreihe in geordneter Weise sammelt.
Ähnliches tat Vaughn mit Punktpaaren auf einer geschlossenen Kurve. Es schließt sich wie die eindimensionale Zahlenlinie nur sich selbst an. Er erkannte, dass die Ebene nicht funktioniert, wenn Sie Punktepaare mit einer Kurve nehmen und daraus eine Figur erstellen (und es spielt keine Rolle, welche die x-Koordinate und welche die y-Koordinate ist). Stattdessen erhalten Sie eine unerwartete Figur - einen Mobius-Streifen , eine zweidimensionale Oberfläche mit nur einer Seite.

Und in gewissem Sinne ist das ziemlich logisch. Um zu verstehen, warum - wählen Sie ein Punktepaar auf der Kurve aus und benennen Sie sie mit x und y. Bewegen Sie sich nun von x nach y, entlang eines Teils der Kurve und gleichzeitig - von y nach x, entlang des Gegenteils. Dabei durchlaufen Sie alle Punktepaare auf der Kurve und beginnen und enden mit einem ungeordneten Paar (x, y). Dies bringt Sie jedoch zum Anfang zurück - nur die endgültige Folge von Punkten ist der ursprünglichen entgegengesetzt. Eine Schleife ungeordneter Punkte, deren Ausrichtung sich in die entgegengesetzte Richtung ändert, ist die Essenz des Möbius-Streifens.
Dieses Band gibt Mathematikern ein neues Objekt, das als Teil des rechteckigen Zapfenproblems analysiert werden kann. Vaughn nutzte diese Tatsache, um zu beweisen, dass es auf jeder Kurve mindestens einen Satz von vier Punkten gibt, die ein Quadrat bilden.
Vierdimensionale Antworten
Der Beweis von Green and Lobb basiert auf Vaughns Arbeit. Es werden jedoch auch einige zusätzliche Erkenntnisse kombiniert, von denen einige relativ neu sind. Der endgültige Beweis ist wie ein präzises Instrument, dessen gewünschtes Ergebnis auf einer sorgfältig durchdachten Kombination von Ideen beruht.
Einer der ersten Hauptbestandteile ihres Beweises war im November 2019, als der Doktorand der Universität Princeton, Cole Hugelmeyer , das Papier veröffentlichteDemonstration einer neuen Methode zur Analyse des von Vaughn verwendeten Möbius-Streifens. Es wurde ein mathematischer Prozess verwendet, der als Verschachtelung bekannt ist. Dabei nehmen wir ein Objekt und projizieren es auf den geometrischen Raum. Infolgedessen nahmen Green und Lobb Hugelmeyers Technik und übertrugen sie auf einen anderen geometrischen Raum. Aber um zu verstehen, was sie getan haben, müssen Sie zuerst verstehen, was er getan hat.
Hier ist ein einfaches Beispiel für das Verschachteln.
Beginnen wir mit einer eindimensionalen Linie. Jeder Punkt einer geraden Linie wird durch eine einzelne Zahl definiert. Jetzt werden wir diese Linie in den zweidimensionalen Raum einbetten - das heißt, wir werden sie auf einer Ebene zeichnen.
Nach dem Einbetten einer geraden Linie in die xy-Ebene wird jeder Punkt darin bereits durch zwei Zahlen bestimmt - die x- und y-Koordinaten, die beschreiben, wo genau sich der Punkt in der Ebene befindet. Sie können die Linie jetzt mithilfe von 2D-Geometrietechniken analysieren.
Hugelmeiers Idee war es, so etwas wie einen Möbius-Streifen zu nehmen, ihn aber in einen 4-Raum einzubetten, in dem Sie mit den Eigenschaften der 4-dimensionalen Geometrie die gewünschten Ergebnisse nachweisen können.
„Grundsätzlich haben Sie einen Mobius-Streifen und müssen jedem Punkt vier Koordinaten zuweisen. Es wird so etwas wie die Adresse eines Punktes im vierdimensionalen Raum sein “, sagte Lobb.
Hugelmeyer wies diese Adressen so zu, dass es einfacher war, zum Hauptziel zu gelangen und Rechtecke auf einer Kurve zu finden. Wir können sagen, dass er jedem Punkt in der Kurve so etwas wie eine Postanschrift zugewiesen hat - Bundesstaat, Stadt, Straßenname und Hausnummer.
Zu diesem Zweck startete er an einem bestimmten Punkt auf dem Mobius-Streifen und nahm die beiden Punkte auf der ursprünglichen geschlossenen Kurve, die sie bezeichnete. Dann fand er den Mittelpunkt des Liniensegments, das diese Punkte verbindet, und bestimmte seine x- und y-Koordinaten. Wir haben die ersten beiden Werte der vierdimensionalen Adresse (Bundesland und Stadt) erhalten.
Dann maß er den Abstand zwischen den beiden ursprünglichen Punkten auf der Kurve. Diese Länge wurde zum dritten Wert der vierdimensionalen Adresse (Straßenname). Schließlich berechnete er den Winkel zwischen dem Liniensegment, das die beiden ursprünglichen Punkte und die x-Achse verbindet. Dieser Winkel wurde zum vierten Wert der vierdimensionalen Adresse (Hausnummer). Diese vier Werte sagen alles über ein Paar von Punkten auf der Kurve aus.

Diese Übung klingt herausfordernd genug, hat sich aber schnell ausgezahlt. Hugelmeyer nahm den beigefügten Mobius-Streifen und drehte ihn um. Der gedrehte Mobius-Streifen hat sich relativ zu seiner ursprünglichen Position bewegt, und die beiden Kopien des Streifens schneiden sich. Da die Drehung im vierdimensionalen Raum stattfand, ist die Selbstschnittform des Möbius-Streifens schwer vorstellbar - aber mathematisch leicht zu beschreiben.
Diese Kreuzung war von großer Bedeutung. Wenn zwei Kopien des Mobius-Streifens übereinandergelegt werden, befinden sich zwei Punktpaare auf der ursprünglichen geschlossenen Kurve, die die vier Eckpunkte des Rechtecks bilden.
Warum?
Denken Sie zunächst daran, dass ein Rechteck als zwei Punktpaare mit einem gemeinsamen Schnittpunkt von Segmenten gleicher Länge dargestellt werden kann, die sie verbinden. Diese Informationen werden in den ersten drei Werten der vierdimensionalen Adresse codiert, die jedem Punkt des verschachtelten Möbius-Streifens zugewiesen sind.
Zweitens können Sie im vierdimensionalen Raum den Mobius-Streifen so entfalten, dass nur eine der Koordinaten jedes Punkts in seiner vierdimensionalen Adresse geändert wird - die Hausnummer ändert sich, aber Straße, Stadt und Bundesland bleiben erhalten. Denken Sie beispielsweise daran, dass sich nur die x-Koordinate ändert, wenn Sie einen Stein nehmen, ihn vor sich positionieren und dann nach rechts bewegen, nicht jedoch y oder z.
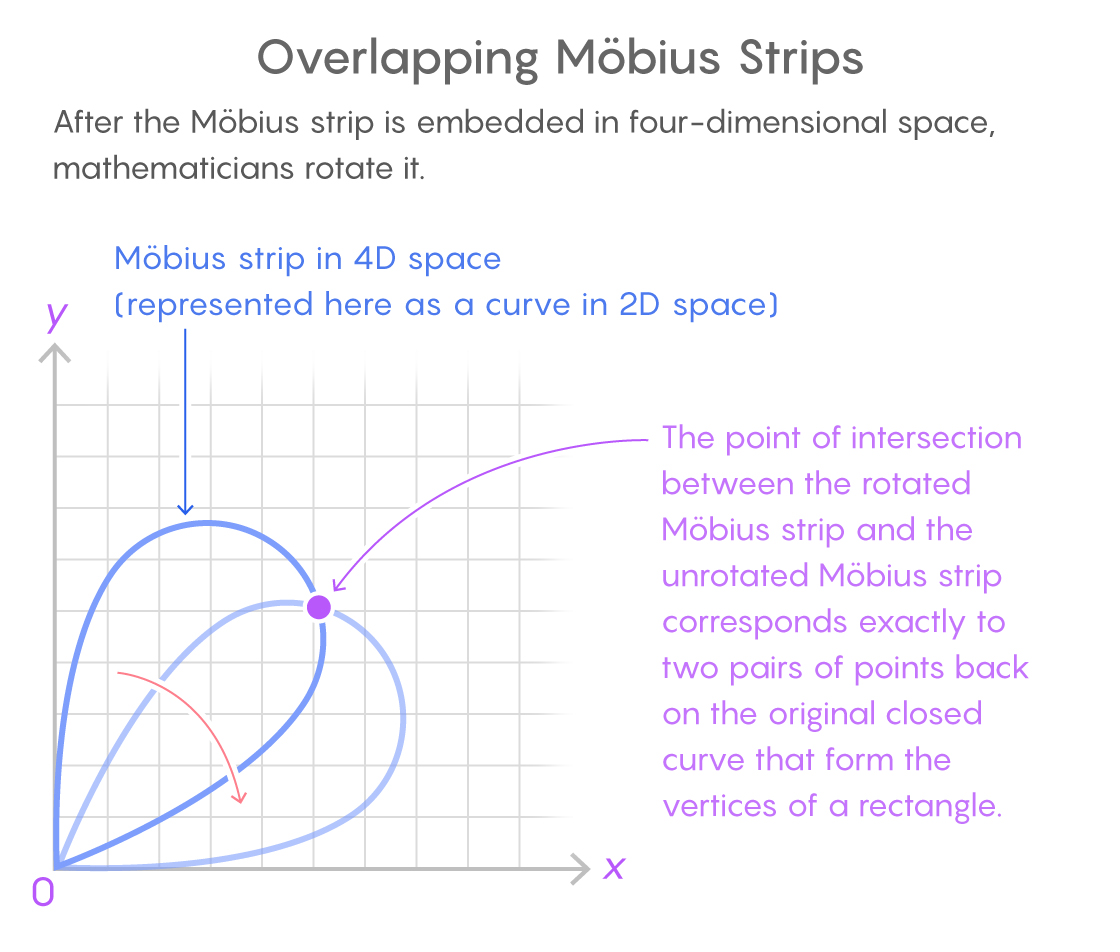
Der Möbius-Streifen im vierdimensionalen Raum wird hier durch eine zweidimensionale Kurve angezeigt. Der Schnittpunkt der beiden Kopien entspricht zwei Punktpaaren auf der ursprünglichen geschlossenen Kurve, die ein Rechteck bilden.
Hugelmeyer erklärte, wie man den Mobius-Streifen im vierdimensionalen Raum dreht, damit sich die beiden Koordinaten, die den Mittelpunkt der die Paare verbindenden Linien angeben, nicht ändern - ebenso wie die Koordinaten, die den Abstand zwischen Punktpaaren angeben. Durch die Drehung wurde nur die letzte Koordinate geändert, die Informationen über den Winkel enthält, in dem sich das die Punkte verbindende Segment befindet.
Infolgedessen entsprach der Schnittpunkt der gedrehten Kopie des Möbius-Streifens und seines Originals genau zwei Punktpaaren, die sich auf einer geschlossenen Kurve befanden, ein gemeinsames Zentrum hatten (Schnittpunkte der sie verbindenden Segmente) und sich im gleichen Abstand voneinander befanden. Das heißt, dieser Schnittpunkt entsprach den vier Eckpunkten des Rechtecks auf der Kurve.
Die Strategie, den Schnittpunkt zweier Räume zu verwenden, um die richtigen Punkte zu finden, wurde lange Zeit bei der Arbeit an den Problemen quadratischer und rechteckiger Stifte verwendet.
"An der Kreuzung dieser Räume befindet sich der gewünschte", sagte Denn. "Viele Beweise aus der Geschichte der quadratischen Stifte haben diese Idee."
Hugelmeyer verwendete eine Kreuzungsstrategie in einer vierdimensionalen Umgebung und bekam mehr als jeder andere vor ihm. Der Mobius-Streifen kann in jedem Winkel von 0 ° bis 360 ° gedreht werden, und er hat bewiesen, dass ein Drittel aller dieser Drehungen zum Schnittpunkt von Original und gedrehter Kopie führt. Dies entspricht der Angabe, dass Sie auf einer geschlossenen Kurve Rechtecke mit einem Drittel aller möglichen Seitenverhältnisse finden können.
"Wir danken Cole dafür, dass er darüber nachgedacht hat, einen Mobius-Streifen in den 4D-Raum zu legen und 4D-Techniken zu verwenden", sagte Green.
Gleichzeitig erwies sich Hugelmeiers Ergebnis als provokativ: Wenn der vierdimensionale Raum für die Arbeit mit diesem Problem so nützlich ist, warum war er dann nur für ein Drittel aller Rechtecke nützlich?
"Schließlich muss es einen Weg geben, die restlichen zwei Drittel zu bekommen", sagte Green. - Aber wie?"
Symplektischer Ansatz
Green und Lobb interessierten sich für das Problem der rechteckigen Stifte, noch bevor die Pandemie sie nach Hause schickte. Im Februar veranstaltete Lobb eine Konferenz am Okinawa Institute of Science and Technology , an der auch Green teilnahm. Das Paar sprach einige Tage über diese Aufgabe. Danach diskutierten sie eine weitere Woche darüber, während sie die Sehenswürdigkeiten von Tokio besichtigten.
"Wir haben nicht aufgehört, dieses Thema zu diskutieren", sagte Lobb. "Wir gingen in Restaurants, Cafés, Museen und hatten von Zeit zu Zeit Gedanken darüber."
Sie setzten ihre Diskussionen fort, selbst nachdem sie in ihren Häusern eingesperrt waren. Sie hofften zu beweisen, dass jede Drehung des Mobius-Streifens einen Schnittpunkt ergeben würde - was dem Auffinden von Rechtecken beliebigen Ausmaßes entspricht.
Mitte April formulierten sie eine Strategie. Es bedeutete, das Band in einen speziellen vierdimensionalen Raum einzubetten. Regelmäßiges Verschachteln bedeutet, dass Sie das gewünschte Objekt auf irgendeine Weise platzieren. Stellen Sie sich vor, wie viele Möglichkeiten Sie haben, eine eindimensionale geschlossene Kurve in eine zweidimensionale Ebene einzubetten - ihre Anzahl ist unendlich, da es unendlich viele Möglichkeiten gibt, einen in einer Schleife gebundenen Faden auf einem Tisch zu platzieren.
Angenommen, die zweidimensionale Oberfläche, in der Sie die Schleife verschachteln, hat eine eigene Struktur. Stellen Sie sich zum Beispiel eine Karte mit Pfeilen (oder Vektoren) vor, die uns anzeigt, in welche Richtung und mit welcher Geschwindigkeit der Wind auf die Erdoberfläche weht. Jetzt haben Sie an jedem Punkt eine 2D-Oberfläche mit zusätzlichen Informationen oder Strukturen.
Dann können Sie Einschränkungen einführen - ein eindimensionales RFP muss auf der Karte platziert werden, damit es immer den Anweisungen der Pfeile auf der Karte folgt.
"Sie begrenzen die Dinge so, dass die Kurve diesen Vektoren folgt", sagte Schwartz. Und jetzt haben Sie weniger Möglichkeiten, die Kurve zu platzieren.

Andere geometrische Räume können andere Einschränkungen auferlegen. Wichtig für die Arbeit von Green und Lobb war das sogenannte. symplektischer Raum .
Dieses geometrische Konzept tauchte erstmals im 19. Jahrhundert auf, als physikalische Systeme wie umlaufende Planeten untersucht wurden. Die Position eines Planeten, der sich im dreidimensionalen Raum bewegt, wird durch drei Koordinaten bestimmt. Aber wie der irische Mathematiker William Rowan Hamilton feststellteAn jedem Punkt des Bewegungspfads des Planeten können Sie auch einen Vektor platzieren, der seinen Impuls angibt.
In den 1980er Jahren entwickelte der sowjetische und russische Mathematiker Vladimir Igorevich Arnold das Studium der symplektischen Geometrie . Er erkannte, dass sich die geometrischen Räume einer symplektischen Struktur beim Drehen häufiger mit sich selbst schneiden als Räume, die keine solche Struktur haben.
Dies war perfekt für Green und Lobb, da sie das Problem der rechteckigen Stifte für alle Proportionen lösen wollten, um zu beweisen, dass sich auch eine gedrehte Kopie eines parametrisierenden Mobius-Streifens häufig schneidet. Also versuchten sie, einen zweidimensionalen Möbius-Streifen in einen vierdimensionalen symplektischen Raum einzubetten. "Eine radikal neue Idee war es, dieses Problem unter dem Gesichtspunkt der symplektischen Geometrie anzugehen", sagte Green. "Und das hat alles verändert."
Ende April stellten Green und Lobb fest, dass es möglich ist, einen Mobius-Streifen in einen vierdimensionalen symplektischen Raum einzubetten, damit er seiner Struktur entspricht. Danach könnten sie symplektische Geometriewerkzeuge verwenden, von denen viele in direktem Zusammenhang mit der Frage der Selbstüberschneidungen stehen.
"Wenn der Möbius-Streifen nach symplektischen Regeln hergestellt werden kann, können einige der symplektischen Theoreme verwendet werden", sagte Lobb.
Green und Lobb waren zuversichtlich, das Ergebnis von Hugelmeyer verbessern zu können - das heißt, beweisen, dass die Kreuzung nicht nur an einem Drittel aller Ecken auftritt. Dies bedeutet, dass aus den Punkten der Kurve Rechtecke mit mehr als einem Drittel aller möglichen Proportionen erstellt werden können.
"Als wir auf diese Idee kamen, wurde klar, dass etwas passieren würde", sagte Lobb.
Ihre Ergebnisse erwiesen sich jedoch als allgemeiner und erschienen viel schneller als erwartet. Alles dank eines seltsamen mathematischen Objekts - der Klein-Flasche , die im Kontext der symplektischen Geometrie eine wichtige Eigenschaft hat.
Klein Flaschenanschluss
Die Klein-Flasche ist eine zweidimensionale Oberfläche, die wie ein modernistischer Krug aussieht. Es hat wie der Mobius-Streifen nur eine Oberfläche und kann durch Kleben von zwei Mobius-Streifen hergestellt werden. Jede Klein-Flasche, die Sie sammeln und auf Ihren Schreibtisch stellen können (wie es viele Mathematiker tun), kreuzt sich selbst. Es ist unmöglich, eine Klein-Flasche in einen dreidimensionalen Raum zu stellen, damit sie sich nicht selbst kreuzt.
"Die Klein-Flasche muss eine Oberfläche sein, aber ihr Griff muss die Flasche durchbrechen, um von außen nach innen zu gelangen", sagte Schwartz.
Dies ist jedoch nicht unbedingt der Fall. Die Klein-Flasche kann im 4D-Raum verschachtelt werden, damit sie sich nicht selbst schneidet. Die vierte Dimension bietet Handlungsspielraum, und die Klein-Flasche kann sich selbst umgehen. Dies kann damit verglichen werden, dass zwei Personen, die in einer eindimensionalen Linie aufeinander zugehen, eine Kollision nicht vermeiden können. Wenn sie jedoch auf einem zweidimensionalen Boden gehen, können sie sich leicht abwenden.

Im Mai erinnerten sich Green und Lobb an eine Tatsache über die Klein-Flasche: Sie kann nicht in einen vierdimensionalen symplektischen Raum eingebettet werden, damit sie sich nicht überschneidet [aus der Arbeit eines anderen russischen Mathematikers, Wsewolod Wiktorowitsch Schewtschischinüber die Lagrange-Einbettung der Klein-Flasche im vierdimensionalen Raum / ca. übersetzt.]. Mit anderen Worten, es gibt keine Klein-Flasche ohne Selbstüberschneidung, die alle Anforderungen eines symplektischen Raums erfüllt. Diese Tatsache wurde zum Schlüssel zum Beweis. "Es war ein Zauberstab", sagte Green.
Und deshalb. Green und Lobb haben bereits gezeigt, dass es möglich ist, einen Mobius-Streifen in einen vierdimensionalen symplektischen Raum einzubetten, damit er seinen Anforderungen entspricht. Sie mussten nur herausfinden, ob jede Umdrehung des Mobius-Streifens die Originalkopie schneidet.
Zwei sich kreuzende Mobius-Streifen entsprechen jedoch einer Klein-Flasche, die sich in einem solchen Raum schneidet. Und wenn Sie den Mobius-Streifen so drehen, dass sich die gedrehte Kopie nicht mit dem Original überschneidet, erhalten Sie eine Klein-Flasche, die sich nicht selbst kreuzt. Aber eine solche Klein-Flasche kann im vierdimensionalen symplektischen Raum nicht existieren. Daher muss sich auch jede mögliche Drehung des verschachtelten Möbius-Streifens schneiden - das heißt, auf jeder geschlossenen glatten Kurve können vier Punkte gefunden werden, die ein Rechteck mit beliebigen Proportionen bilden.
Das Ende des Beweises trifft den Leser wie eine Lawine.
"Es wird zuerst eingerichtet, eingerichtet, eingerichtet und dann grunzt, und der Beweis ist fertig", sagte Denn.
Der Beweis von Green and Lobb ist ein gutes Beispiel dafür, wie oft die Lösung eines Problems davon abhängt, den richtigen Standpunkt zu finden. Generationen von Mathematikern waren nicht in der Lage, diese Version des rechteckigen Zapfenproblems anzugehen, weil sie versucht haben, es unter traditionelleren geometrischen Bedingungen zu lösen. Als Green und Lobb das Problem in die symplektische Welt brachten, war es leicht zu lösen.
"Diese Probleme, die in den 1910er und 1920er Jahren auftraten, hatten keine geeignete Plattform, um darüber nachzudenken", sagte Green. "Und jetzt beginnen wir zu verstehen, dass es sich tatsächlich um verborgene Inkarnationen des Phänomens der Symplektizität handelt."