Kollisionserkennung und der Teilungsachsensatz

Heutzutage sind Computer leistungsstarke Computer

, die Millionen von Vorgängen pro Sekunde ausführen können. Und natürlich kann man nicht auf die Simulation der realen oder Spielwelt verzichten. Eines der Probleme der Computermodellierung und -simulation besteht darin, die Kollision zweier Objekte zu bestimmen, deren Lösung durch den Satz auf der Trennachse realisiert wird.







Hinweis. Der Artikel wird ein Beispiel mit 2 Parallelepipeds (im Folgenden - Würfel) geben, aber die Idee für andere konvexe Objekte bleibt erhalten.

Hinweis. Die gesamte Implementierung erfolgt in Unity.

Akt 0. Allgemeine Theorie

Zunächst müssen Sie sich mit dem " Theorem der trennenden Hyperebene " vertraut machen . Es wird die Grundlage des Algorithmus sein.



Satz. Zwei konvexe Geometrien schneiden sich nicht genau dann, wenn sich zwischen ihnen eine Hyperebene befindet, die sie trennt. Die zur Teilungshyperebene orthogonale Achse

wird als Teilungsachse bezeichnet, und die Projektionen der Figuren darauf schneiden sich nicht.





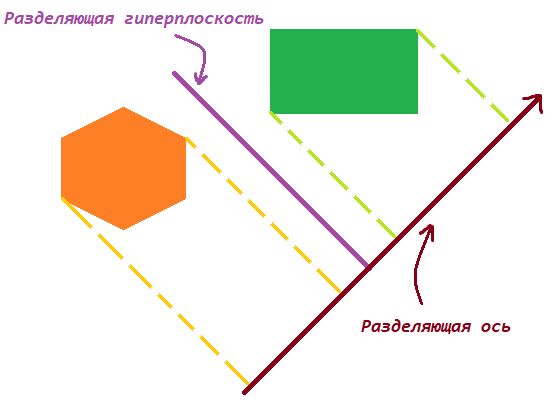
Teilungsachse (2D-Fall)





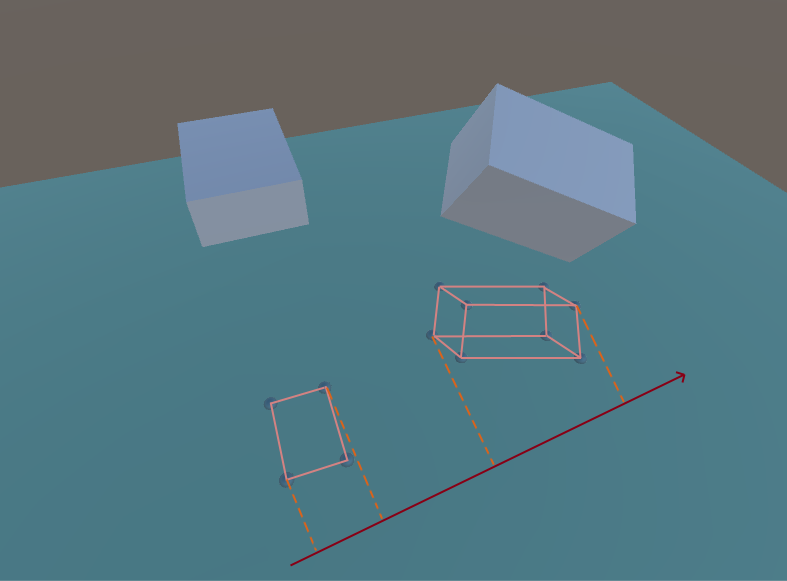
Teilungsachse (3D-Fall)

Möglicherweise stellen Sie fest, dass sich die Projektionen auf der Teilungsachse nicht schneiden.



Eigentum. Die potentielle Teilungsachse wird in den folgenden Sätzen sein:

• Flugzeugnormen für jeden Würfel (rot)
• Vektorprodukt der Kanten der Würfel $$$\{[\vec{x},\vec{y}] : x∈X, y∈Y\}$,

   Dabei ist X die Kante des ersten Würfels (grün) und Y der zweite (blau).







Wir können jeden Würfel mit den folgenden Eingabedaten beschreiben:

• Würfelmittenkoordinaten
• Würfelabmessungen (Höhe, Breite, Tiefe)
• Quaternion des Würfels

Erstellen wir hierfür eine zusätzliche Klasse, deren Instanzen Informationen über den Cube liefern.

public class Box
{
    public Vector3 Center;
    public Vector3 Size;
    public Quaternion Quaternion;

    public Box(Vector3 center, Vector3 size, Quaternion quaternion)
    {
       this.Center = center;
       this.Size = size;
       this.Quaternion = quaternion;
    }
    //  , 
    //      GameObject
    public Box(GameObject obj)
    {
        Center = obj.transform.position;
        Size = obj.transform.lossyScale;
        Quaternion = obj.transform.rotation;
    }

}

Akt 1. Quaternionen

Wie so oft kann sich ein Objekt im Raum drehen. Um die Koordinaten der Eckpunkte unter Berücksichtigung der Drehung des Würfels zu ermitteln, müssen Sie verstehen, was eine Quaternion ist.



Quaternion ist eine hyperkomplexe Zahl, die die Drehung eines Objekts im Raum bestimmt.

$$

$$w+xi+yj+zk$$

Der Imaginärteil (x, y, z) stellt einen Vektor dar, der die Drehrichtung definiert. Der

Realteil (w) definiert den Winkel, unter dem die Drehung ausgeführt wird.



Der Hauptunterschied zu allen üblichen Euler-Winkeln besteht darin, dass wir einen Vektor haben, der die Drehrichtung bestimmt, als drei linear unabhängige Vektoren, die das Objekt in drei Teilräumen drehen.



Ich empfehle zwei Artikel, die detaillierter auf Quaternionen eingehen:



Eins

Zwei



Nachdem wir ein minimales Verständnis der Quaternionen haben, wollen wir verstehen, wie ein Vektor gedreht wird, und die Funktion des Drehens eines Vektors mit einer Quaternion beschreiben.



Vektorrotationsformel

$$

$$\vec{v}' = q * \vec{v} * \overline{q}$$

$$$\vec{v}'$ Ist der erforderliche Vektor

$$$\vec{v}$ - Originalvektor

$$$q$ - Quaternion

$$$\overline{q}$- inverse Quaternion



Lassen Sie uns zunächst das Konzept der inversen Quaternion orthonormal angeben - es ist eine Quaternion mit einem Imaginärteil des entgegengesetzten Vorzeichens.



$$$q = w+xi+yj+zk$

$$$\overline{q} = w-xi-yj-zk$



Lass uns zählen $$$\vec{v} * \overline{q}$



$$$M = \vec{v}*\overline{q} = (0 + v_xi + v_yj + v_zk)(q_w - q_xi - q_yj - q_zk) =$

$$$=\color{red}{v_xq_wi} + \color{purple}{v_xq_x} - \color{blue}{v_xq_yk} + \color{green}{v_xq_zj} +$

$$$+\color{green}{v_yq_wj} + \color{blue}{v_yq_xk} + \color{purple}{v_yq_y} - \color{red}{v_yq_zi} +$

$$$+\color{blue}{v_zq_wk} - \color{green}{v_zq_xj} + \color{red}{v_zq_yi} + \color{purple}{v_zq_z}$



Jetzt werden wir die einzelnen Komponenten ausschreiben und aus diesem Produkt eine neue Quaternion sammeln

$$$M = u_w+u_xi+u_yj+u_zk$

$$$u_w = \color{purple}{v_xq_x + v_yq_y + v_zq_z}$

$$$u_xi = \color{red}{(v_xq_w - v_yq_z + v_zq_y)i}$

$$$u_yj = \color{green}{(v_xq_z + v_yq_w - v_zq_x)j}$

$$$u_zk = \color{blue}{(-v_xq_y + v_yq_x + v_zq_w)k}$



Zählen wir den Rest, d.h. $$$q*M$und erhalten Sie den gewünschten Vektor.



Hinweis. Um die Berechnungen nicht zu überladen, präsentieren wir nur den Imaginärteil (Vektor) dieses Produkts. Immerhin ist sie es, die den gewünschten Vektor charakterisiert.



$$$\vec{v}' = q*M = (q_w + q_xi + q_yj + q_zk)(u_w + u_xi + u_yj + u_zk) =$

$$$= \color{red}{q_wu_xi} + \color{green}{q_wu_yj} + \color{blue}{q_wu_zk} +$

$$$+\color{red}{q_xu_wi} + \color{blue}{q_xu_yk} - \color{green}{q_xu_zj} +$

$$$+\color{green}{q_yu_wj} - \color{blue}{q_yu_xk} + \color{red}{q_yu_zi} +$

$$$+\color{blue}{q_zu_wk} +\color{green}{q_zu_xj} -\color{red}{q_zu_yi}$



Sammeln wir die Komponenten des Vektors



$$$v_x' = \color{red}{q_wu_x + q_xu_w + q_yu_z - q_zu_y}$

$$$v_y' = \color{green}{q_wu_y - q_xu_z + q_yu_w + q_zu_x}$

$$$v_z' = \color{blue}{q_wu_z + q_xu_y - q_yu_x + q_zu_w}$



$$$v' = (v_x', v_y', v_z')$

Somit wird der erforderliche Vektor erhalten. Schreiben Sie den



Code:

private static Vector3 QuanRotation(Vector3 v,Quaternion q)
{
        float u0 = v.x * q.x + v.y * q.y + v.z * q.z;
        float u1 = v.x * q.w - v.y * q.z + v.z * q.y;
        float u2 = v.x * q.z + v.y * q.w - v.z * q.x;
        float u3 = -v.x * q.y + v.y * q.x + v.z * q.w;
        Quaternion M = new Quaternion(u1,u2,u3,u0);
        
        Vector3 resultVector;
        resultVector.x = q.w * M.x + q.x * M.w + q.y * M.z - q.z * M.y;  
        resultVector.y = q.w * M.y - q.x * M.z + q.y * M.w + q.z * M.x;
        resultVector.z = q.w * M.z + q.x * M.y - q.y * M.x + q.z * M.w;
        
        return resultVector;
}

Akt 2. Finden der Eckpunkte eines Würfels

Wenn Sie wissen, wie ein Vektor mit einem Quaternion gedreht wird, ist es nicht schwierig, alle Eckpunkte des Würfels zu finden.



Fahren wir mit der Funktion fort, die Eckpunkte eines Würfels zu finden. Definieren wir die Basisvariablen.

private static Vector3[] GetPoint(Box box)
{
        //    
        Vector3[] point = new Vector3[8];

        // 
        //....

        return point;
}

Als nächstes müssen Sie einen Punkt (Ankerpunkt) finden, von dem aus es am einfachsten ist, andere Eckpunkte zu finden.



Subtrahieren Sie die Hälfte der Würfelabmessung von der Mittelkoordinate und fügen Sie dann eine Würfelabmessung zum Drehpunkt hinzu.

//...
        //  
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//     
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//...

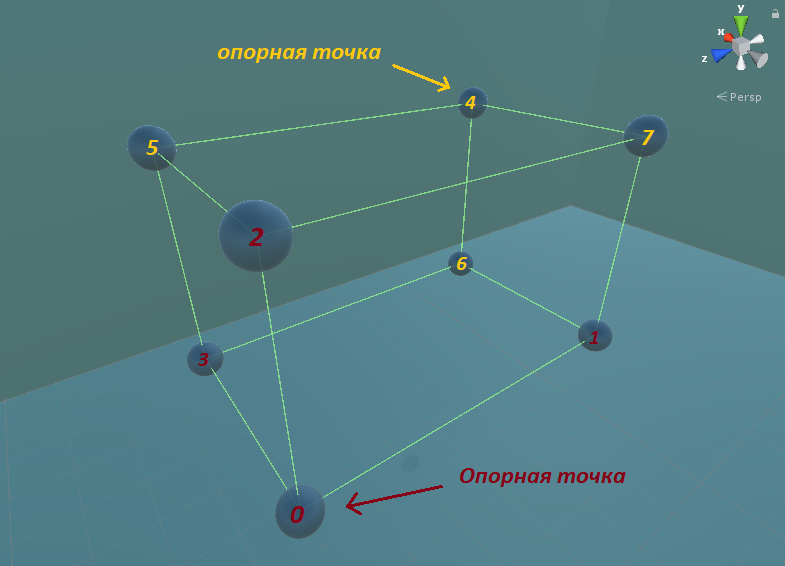
Wir können sehen, wie die Punkte gebildet werden



Nachdem wir die Koordinaten der Eckpunkte gefunden haben, ist es notwendig, jeden Vektor um die entsprechende Quaternion zu drehen.

//...

        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//    

            point[i] = QuanRotation(point[i], box.Quaternion);//

            point[i] += box.Center;// 
        }

//...

Fahren wir mit den Projektionen fort.

Akt 3. Suche nach Teilungsachsen

Der nächste Schritt besteht darin, den Satz von Achsen zu finden, die behaupten, geteilt zu werden.

Denken Sie daran, dass es in den folgenden Sets zu finden ist:

• Flugzeugnormalen jedes Würfels (rot)
• Vektorprodukt der Kanten der Würfel $$$\{[\vec{x},\vec{y}[ : x∈X, y∈Y\}$Dabei ist X die Kante des ersten Würfels (grün) und Y der zweite (blau).

Um die erforderlichen Achsen zu erhalten, reichen vier Eckpunkte des Würfels aus, die ein orthogonales Vektorsystem bilden. Diese Eckpunkte befinden sich in den ersten vier Zellen des Punktarrays, das wir im zweiten Akt gebildet haben.







Es ist notwendig, die von den Vektoren erzeugten Ebenennormalen zu finden:

• $$$\vec{a}$ und $$$\vec{b}$
• $$$\vec{b}$ und $$$\vec{c}$
• $$$\vec{a}$ und $$$\vec{c}$

Dazu ist es notwendig, die Kantenpaare des Würfels zu durchlaufen, damit jede neue Probe eine Ebene bildet, die orthogonal zu allen zuvor erhaltenen Ebenen ist. Es war unglaublich schwierig für mich zu erklären, wie es funktioniert, deshalb habe ich zwei Versionen des Codes bereitgestellt, um Ihnen das Verständnis zu erleichtern.





Aber Sie können es einfacher machen:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //
        Vector3 A;
        Vector3 B;

	//  
        List<Vector3> Axis = new List<Vector3>();

	//   
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//  
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //...
}

Wir müssen auch alle Vektorprodukte der Würfelkanten finden. Dies kann durch eine einfache Suche organisiert werden:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //...
        // 
        //... 

       //    
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}

Akt 4. Projektionen auf der Achse

Wir sind zum wichtigsten Punkt gekommen. Hier müssen wir die Projektionen der Würfel auf allen möglichen Teilungsachsen finden. Der Satz hat eine wichtige Konsequenz: Wenn sich Objekte schneiden, ist die Achse (normal) der Kollision die Achse (auf der der Schnittpunkt der Projektion der Würfel minimal ist) und die Länge des Schnittpunktsegments die Eindringtiefe.



Erinnern Sie sich jedoch zunächst an die Formel für die skalare Projektion des Vektors v auf den Einheitsvektor a :

$$

$$proj_\left\langle \vec{a} \right\rangle \vec{v} = \frac{(\vec{v},\vec{a})}{| \vec{a} |}$$

private static float ProjVector3(Vector3 v, Vector3 a)
{
        a = a.normalized;
        return Vector3.Dot(v, a) / a.magnitude;
        
}

Nun werden wir eine Funktion beschreiben, die den Schnittpunkt von Projektionen auf den Kandidatenachsen bestimmt.



Die Eingabe besteht aus den Eckpunkten zweier Würfel und einer Liste möglicher Teilungsachsen:

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
           //     
           //         
        }
        //       ,   ,    
        //    .
}

Die Projektion auf die Achse wird durch zwei Punkte festgelegt, die Maximal- und Minimalwerte auf der Achse selbst haben:







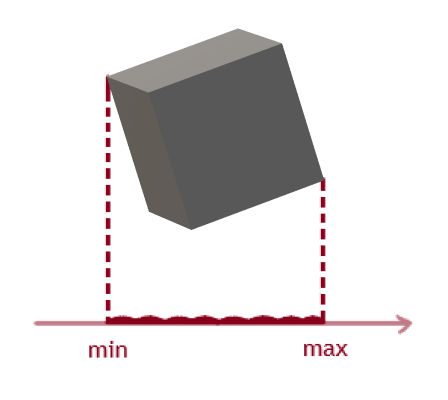
Als Nächstes erstellen wir eine Funktion, die die Projektionspunkte jedes Würfels zurückgibt. Es werden zwei Rückgabeparameter benötigt, ein Scheitelpunktarray und eine potenzielle Teilungsachse.

private static void ProjAxis(out float min, out float max, Vector3[] points, Vector3 Axis)
{
        max = ProjVector3(points[0], Axis);
        min = ProjVector3(points[0], Axis);
        for (int i = 1; i < points.Length; i++)
        {
            float tmp = ProjVector3(points[i], Axis);
            if (tmp > max)
            {
                max = tmp;
            }

            if (tmp < min)
            {
                min= tmp;
            }
        }
}

Wenn Sie diese Funktion ( ProjAxis ) anwenden , erhalten Sie die Projektionspunkte jedes Würfels.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
            //  a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //  b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);
            
            //...
        }
        //...
}

Als nächstes bestimmen wir basierend auf den Projektionsscheitelpunkten den Schnittpunkt der Projektionen:







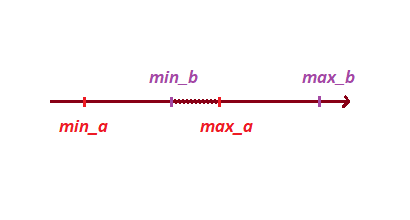
Um dies zu tun, setzen wir unsere Punkte in ein Array und sortieren es. Diese Methode hilft uns, nicht nur den Schnittpunkt, sondern auch die Tiefe des Schnittpunkts zu bestimmen.

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);

Beachten Sie die folgende Eigenschaft:



1) Wenn sich die Segmente nicht schneiden , ist die Summe der Segmente um die gebildeten Extrempunkte kleiner als das Segment:







2) Wenn sich die Segmente schneiden , ist die Summe der Segmente um die gebildeten Extrempunkte größer als das Segment:







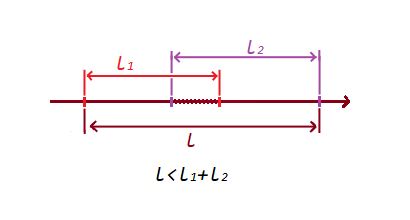
Mit dieser einfachen Bedingung haben wir den Schnittpunkt und den Nichtschnittpunkt überprüft Segmente.



Wenn es keinen Schnittpunkt gibt, ist die Schnitttiefe Null:

            //...
            // 
            float sum = (max_b - min_b) + (max_a - min_a);
            //  
            float len = Math.Abs(p[3] - p[0]);
            
            if (sum <= len)
            {
                //  
                //  
                return Vector3.zero;
            }
            //,        
            //....

Es reicht also aus, mindestens einen Vektor zu haben, auf dem sich die Projektionen der Würfel nicht schneiden, dann schneiden sich die Würfel selbst nicht. Wenn wir die Teilungsachse finden, können wir daher die Überprüfung der verbleibenden Vektoren überspringen und den Algorithmus beenden.



Beim Schnittpunkt von Würfeln ist alles etwas interessanter: Die Projektion der Würfel auf alle Vektoren schneidet sich, und wir müssen den Vektor mit dem minimalen Schnittpunkt definieren.



Lassen Sie uns diesen Vektor vor der Schleife erstellen und den Vektor mit der minimalen Länge darin speichern. Somit erhalten wir am Ende des Zyklus den gewünschten Vektor.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
                //...
        }
        // ,      ,  
        return norm;
{

Und jedes Mal, wenn wir die Achse finden, auf der sich die Projektionen schneiden, prüfen wir, ob sie die kleinste unter allen ist. Wir multiplizieren eine solche Achse mit der Länge des Schnittpunkts und das Ergebnis ist die gewünschte Normalen (Richtung) des Schnittpunkts der Würfel.



Ich habe auch eine Definition der Ausrichtung der Normalen in Bezug auf den ersten Würfel hinzugefügt.

//...
if (sum <= len)
{
   //  
   //   
   return new Vector3(0,0,0);
}
//,        

//  -    2  1    
//(.       )
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
   norm = Axis[j] * dl;
   // 
   if(points[0] != min_a)
   norm = -norm;
}
//...

Fazit

Das Projekt mit Implementierung und Beispiel wird auf GitHub hochgeladen und kann hier angezeigt werden .



Mein Ziel war es, meine Erfahrungen bei der Lösung von Problemen im Zusammenhang mit der Bestimmung der Schnittpunkte zweier konvexer Objekte zu teilen. Und es ist auch zugänglich und verständlich, über diesen Satz zu erzählen.