
Geboren zum Krabbeln kann nicht fliegen. Dieser Satz kann sowohl im metaphorischen als auch im wörtlichen Sinne verwendet werden, da Kreaturen ohne Flügel (oder Körperteile mit ähnlicher Funktionalität) den Himmel wirklich nicht erobern können. Zumindest die meisten von ihnen. Die Regel wäre nicht die Regel, wenn es keine Ausnahmen gäbe. In Bezug auf flügellose Flüge gibt es auch Ausnahmen - geschmückte Baumschlangen ( Chrysopelea)). Vertreter dieser Art von Schlange können aufsteigen - eine äußerst nützliche Fähigkeit, wenn man bedenkt, dass sie in den Kronen von Bäumen hoch über dem Boden leben. Wissenschaftler der Virginia Polytechnic University (USA) beschlossen, den Flug eines Drachens aus kinematischer Sicht zu betrachten. Welche anatomischen Merkmale ermöglichen es Schlangen zu fliegen (genauer gesagt kontrollierter Fall), was passiert aus kinematischer Sicht während des Fluges und wie kann diese Studie der Robotik helfen? Die Antworten auf diese Fragen erwarten uns im Bericht der Wissenschaftler. Gehen.
Grundlagen der Forschung
Verzierte Baumschlangen sind eine Gattung von Serpentinenschlangen, die in Süd- und Südostasien vorkommen. Vertreter dieser Gattung können sich nicht großer Dimensionen (Körperlänge nur von 0,6 bis 1,5 m) und tödlichem Gift rühmen. Obwohl die Beute, die sie tagsüber jagen, dieser nicht zustimmen würde. Angesichts des Lebensraums (Baumkronen) haben diese Schlangen äußerst wenige Feinde, da sie kein besonderes Bedürfnis nach einem starken Gift haben. Außerdem haben sie eine viel effektivere Taktik - sie wissen, wie man plant.

Fliegende Schlangen, wie sie im Volksmund genannt werden, kriechen mit harten Schuppen entlang ihres Bauches durch Bäume und ermöglichen es ihnen, sich vertikal zu bewegen. Wenn sich die Schlange von einem Baum zum anderen bewegen möchte, kriecht sie zuerst bis zum Rand des Astes und faltet dann ihren Körper in Form des lateinischen Buchstabens "J", um zu zielen (bestimmen Sie den gewünschten Startwinkel und Landeplatz). Die Schlange sagt "Lass uns gehen" und drückt ihren Körper nach vorne und oben, zieht ihren Magen ein und ragt aus ihren Rippen heraus (so dass ihr Körper flacher und leicht konkav wird). Während der Planung macht die Schlange ständig Serpentinenbewegungen des Körpers von einer Seite zur anderen, wodurch sie den Flug kontrollieren und sanft landen kann.
Seitenansicht einer langen Planung einer fliegenden Schlange Chrysopelea paradisi.
Ein zusätzlicher Vorteil der für Schlangen so ungewöhnlichen Bewegungsmethode ist die beeindruckende Energieeinsparung, da der Flug viel schneller (und sicherer) ist als das langsame Kriechen von Baum zu Baum auf dem Boden. Allein aus dieser kurzen Beschreibung geht hervor, dass die Mechanik des Drachenflugs viele wichtige Elemente enthält. Startwinkel, Körperform während des Starts und Fluges, Körperbewegung im Flug usw.
Der auffälligste Aspekt des Fluges der Schlange, insbesondere für Beobachter, ist die Wellenbewegung des Körpers. Diese Technik wird von vielen Kreaturen auf dem Planeten verwendet, um sich auf Land und Wasser zu bewegen. Sie müssen nicht weit gehen, denn die Schlangen selbst nutzen es perfekt. Wissenschaftler stellen fest, dass die wellenförmige Bewegung an Land und auf dem Wasser recht gut untersucht wurde, aber solche Pirouetten in der Luft sind immer noch ein Rätsel.
Bei Chrysopelea- Schlangen ist die Welligkeit durch eine S-förmige Körperform, eine niedrige Wellenfrequenz (1–2 Hz) und einen abgeflachten aerodynamischen Querschnitt des Körpers gekennzeichnet.
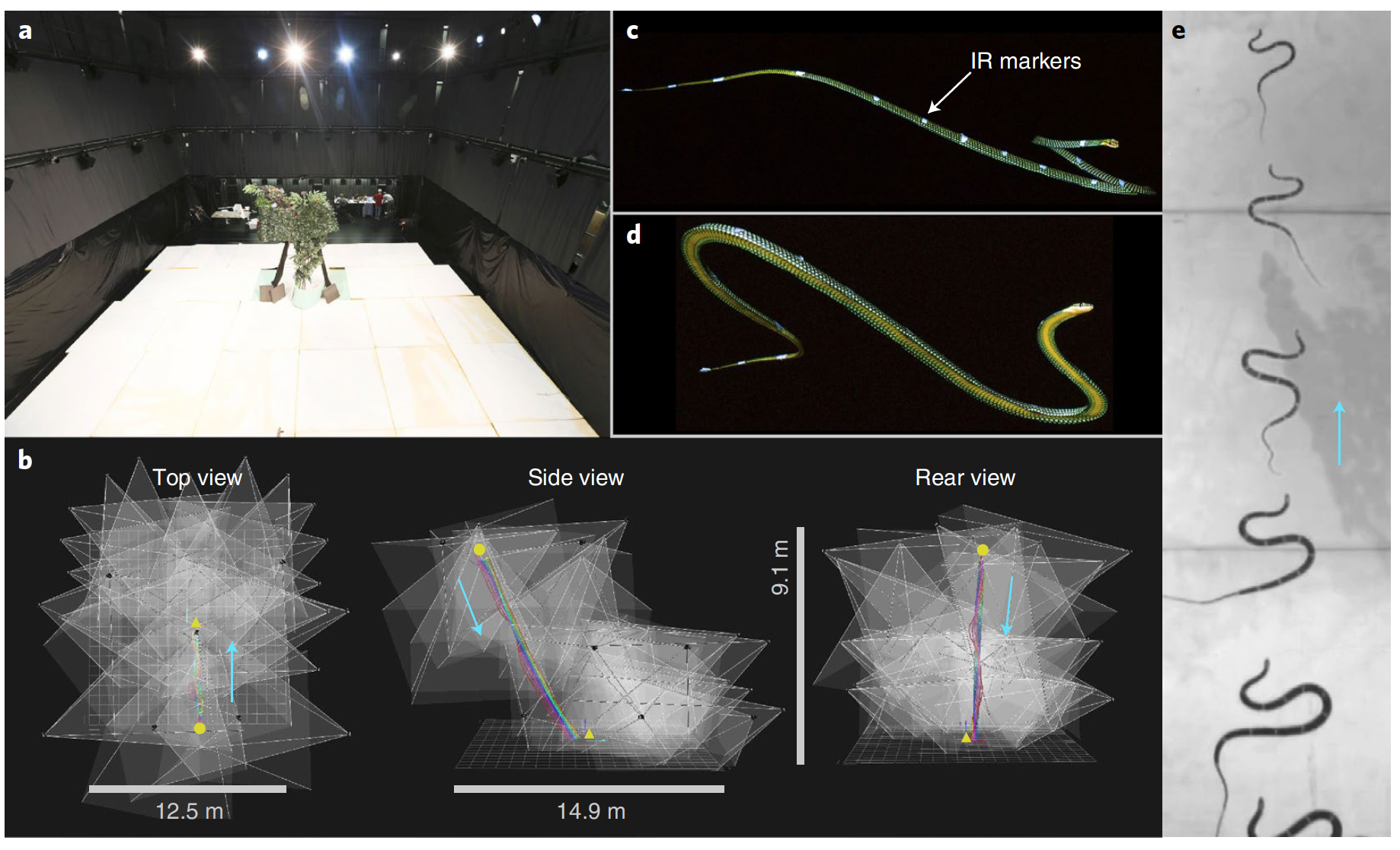
Bild Nr. 1
Tatsächlich baut die luftige Welligkeit den Körper der Schlange kontinuierlich wieder auf und verwandelt ihn in seine Form in einen Flügel ( 1)). Frühere Untersuchungen haben gezeigt, dass fliegende Drachen im Flug immer Wellenbewegungen ausführen. Es bleibt jedoch unklar, ob die Welligkeit der Hauptteil eines erfolgreichen Fluges ist oder nur eine Gewohnheit, d.h. Der Verhaltensaspekt der Bewegung an Land wanderte ohne Absichten in die Flucht.
Wenn wir die Welligkeit an Land und auf dem Wasser berücksichtigen, können wir davon ausgehen, dass sie einen Schub in der Luft erzeugt. Auf festen Medien tritt aufgrund der verteilten Kontaktkräfte über die ventralen und lateralen Bereiche des Körpers eine wellenförmige Bewegung auf, und in Wasser bewirkt die Verschiebung oder Absorption von Flüssigkeit entlang des Körpers eine Vorwärtsbewegung. In beiden Fällen wirkt die reine Antriebskraft hauptsächlich in der Welligkeitsebene. Die Modulation des Körpers außerhalb der Ebene (in vertikaler Richtung) kann für sekundäre Zwecke verwendet werden, z. B. zum Verringern des Widerstands oder zum Erhöhen der Normalkraft.
Für Drachenflüge erfordert eine erfolgreiche Planung jedoch die Erzeugung aerodynamischer Kräfte, die erforderlich sind, um das Gewicht des Tieres auszugleichen. Die Auftriebs- und Widerstandskräfte werden durch die Luft erzeugt, die durch den abgeflachten Körper strömt, wenn sie durch die Schwerkraft nach unten beschleunigt wird, und die durch Muskelkontraktionen verursachte Hin- und Herbewegung erhöht wahrscheinlich nicht die Krafterzeugung.
Vorderansicht des Starts und der Abflachung einer fliegenden Schlange Chrysopelea paradisi.
Die resultierenden aerodynamischen Kräfte müssen außerhalb der Ebene der Welligkeit wirken, und die Welligkeit selbst muss die Verteilung der Kräfte auf den Körper der Schlange ständig ändern. Es ist auch zu bedenken, dass Drachen nicht nur horizontal, sondern auch vertikal "flattern" können. Dies bedeutet, dass es im Flugmodell der Schlange sowohl Nickelemente * als auch Rollelemente * gibt .
Pitch * - Winkelbewegung relativ zur horizontalen Querträgheitsachse.In dieser Studie beschlossen die Wissenschaftler, die Rolle der Welligkeit beim Drachenflug genauer zu untersuchen. Mithilfe von Hochgeschwindigkeits-Schlangenflugaufzeichnungen konnten Wissenschaftler die Welligkeit in der Luft quantifizieren. Die erhaltenen Daten ermöglichten es, ein genaues dreidimensionales Modell des Drachenfluges zu erstellen.
Roll * - Winkelbewegung um seine Längsachse.
Forschungsergebnisse
Die Luftwelligkeit besteht aus einer Reihe von Wellen horizontaler und vertikaler Biegung. 11-17 Marker wurden entlang des Körpers von Schlangen (7 Individuen) platziert, die am Schießen des Fluges teilnahmen (hohe Startfläche von 8,3 m). Durch die Bewertung der Positionsänderungen dieser Markierungen können Sie die Struktur der Welligkeit während des Flugs genau bestimmen.
Draufsicht des Testgleitens einer fliegenden Schlange Chrysopelea paradisi.
Infrarotmarkierungen, die beim Gleiten einer fliegenden Schlange, Chrysopelea paradisi, erhalten wurden.
Nach 36 praktischen Beobachtungen erstellten die Wissenschaftler ein 3D-Modell des Körpers der Schlange ( r ).
Entwicklung eines 3D-Modells des Chrysopelea paradisi-Flugdrachens anhand von Bewegungserfassungsdaten.
Mit dem Tangentenvektor (t̂ = ∂r / ∂s) konnte die Welligkeit in zwei eckige Biegewellen zerlegt werden, die sich entlang des Körpers bewegen.
Horizontale und vertikale Wellen sind durch die folgenden Formeln gegeben:
θ̅ (s, t) = -tan -1 t̂ x / t̂ y
und
ψ̅ (s, t) = sin -1 t̂ z
wobei θ̅ (s, t) und ψ̅ (s, t) ) Sind die lokalen Winkel, die der Körper relativ zur horizontalen und vertikalen Richtung bildet, als Funktion der Bogenlänge s und der Zeit t.
Die Daten zeigen, dass Drachen zwei Wellen verwenden: eine horizontale Welle mit einer großen Amplitude und eine vertikale Welle mit einer niedrigeren Amplitude, die beide nacheinander vom Kopf bis zum Schwanz über den Körper laufen (Bild Nr. 2).

Bild Nr. 2
Diese Wellen bilden sich nach dem anfänglichen Übergang, wenn die Schlange in einer relativ geraden Pose springt und dann eine charakteristische S-förmige Pose für die Planung bildet.
Es gibt vier Merkmale der Luftwelligkeit, die eine vertikale Welle mit einer horizontalen Welle verbinden ( 2a ). Erstens hat die vertikale Welle räumliche und zeitliche Frequenzen, die doppelt so hoch sind wie die horizontale Welle. Dies zeigt an, dass der Körper doppelt so viele vertikale Biegungen aufweist wie seitliche Biegungen ( 2a ,2e ). Zweitens können die U-Biegungen am Körper eines fliegenden Drachens als Nulldurchgänge auf dem Biegewinkelplot ( 2b ) identifiziert werden . Drittens sind diese Überkreuzungen vertikale Wellenhöhen, was anzeigt, dass die horizontalen und vertikalen Wellen um 90 ° phasenverschoben sind. Viertens tritt die maximale Biegung außerhalb der Ebene an den U-Biegungen und ungefähr in der Mitte der geraden Segmente auf. Bei U-Biegungen faltet sich der Querschnitt des "Flügels" der Schlange aufgrund der Bewegung des Körpers außerhalb der Ebene ( 1c , 1d ).
Die Form der Wanderwellen ändert sich im Laufe der Zeit, wenn der Drachen beschleunigt und aerodynamische Kräfte erzeugt. Einige Merkmale sind jedoch noch häufig. Die horizontale Welle ist eine Sinuskurve mit flacher Spitze, deren Amplitude (80-120 °) von der Anzahl der räumlichen Perioden abhängt, wobei weniger Perioden zu höheren horizontalen Biegewinkeln führen. Die vertikale Welle ist eine Sinuskurve mit schmaler Spitze und breiten Tälern mit Amplituden im Bereich von 20 ° bis 45 °.
Die Quantifizierung der räumlichen und zeitlichen Eigenschaften der Wellen zeigte, dass Drachen horizontale Wellen mit 1-1,5 räumlichen Perioden und einer Wellenfrequenz von 1-1,7 Hz und vertikale Wellen mit 2-3 räumlichen Perioden und einer Wellenfrequenz von 2-3,4 Hz verwenden.
Es gibt eine zusätzliche Komponente in der Luftwelligkeit, die Wissenschaftler als "dorsoventrale Biegung" bezeichnet haben und die die Auf- und Abbewegung des Hinterkörpers relativ zum Kopf darstellt. Der Neigungswinkel dieser Biegung betrug -20 ° bis 30 °. Die dorsoventrale Biegung war bei den beobachteten Flügen immer vorhanden, hatte jedoch keinen signifikanten Zusammenhang mit der Anzahl der räumlichen Perioden.
Um den Grad des Einflusses der Beziehung zwischen horizontalen und vertikalen Wellen sowie den Einfluss der dorsoventralen Biegung auf die Flugdynamik genau zu bestimmen, erstellten die Wissenschaftler ein anatomisch genaues Modell einer Schlange im Flug. Die Kontrolle über das Modell ermöglicht es Wissenschaftlern, systematisch zu überprüfen, wie sich die Komponenten der Welligkeit (die Amplitude der horizontalen Welle, die Anzahl der räumlichen Perioden und die Frequenz der Welligkeit) auf die kurzfristige und langfristige Dynamik der Planung auswirken.
Die horizontale Welle wird als Sinus mit einer flachen Spitze mit großer Amplitude modelliert, und die vertikale Welle wird als Sinus mit kleiner Amplitude modelliert:
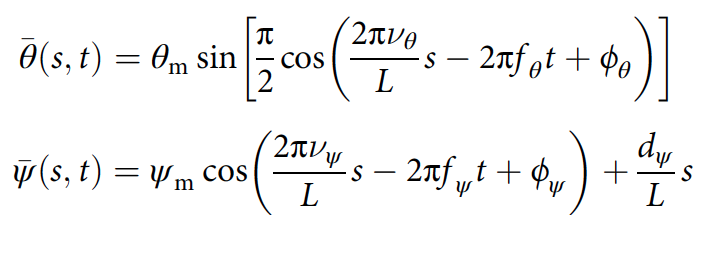
wobei θ m und ψ m die maximalen horizontalen und vertikalen Biegewinkel sind; ν ist die Anzahl der räumlichen Perioden; f - Wellenfrequenz; ϕ - Phasenverschiebung; d ψ - dorsoventraler Biegewinkel; L - Körperlänge ( 2f , 2g ).
Horizontale und vertikale Wellen werden in kinematischer Daten (bezogen 2 ): & ngr; ψ = 2 & ngr; θ , f ψ = 2f θ und & phiv; ψ = 2 (& phiv; θ- π / 2). Dies vereinfacht das Modell erheblich auf 5 Variablen, die die Form des Körpers bestimmen: θ m , ψ m , ν θ , f θ und d ψ .
Die Position r = [x, y, z] des Körpers relativ zum Massenmittelpunkt wird wie folgt berechnet: ∂ s x = cosψ̅sinθ̅, ∂ s y = -cosψ̅cosθ̅ und ∂ s z = sinψ̅.
Die Position des Massenschwerpunkts R 0 und die Ausrichtung des Körpers ( Gierwinkel * , Nick- und Rollwinkel ) werden durch Integration der Gleichungen von Translations- und Rotationsbewegung bestimmt.
Gieren * - Winkelbewegungen um die vertikale Achse.
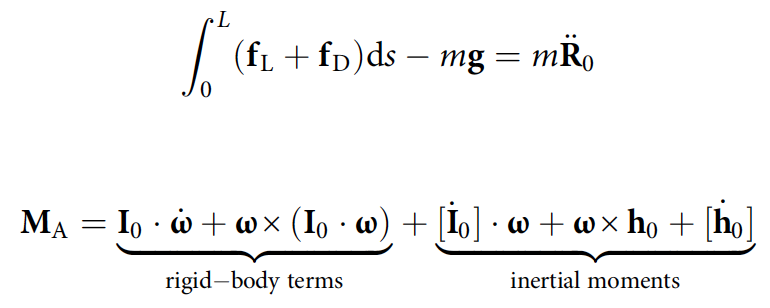
wobei f L und f D - infinitesimale Hub- und Widerstandskräfte; M A - aerodynamischer Moment; m ist die Masse der Schlange.
Um zu bestätigen, dass das mathematische Modell physikalisch realistische Ergebnisse liefert, simulierten die Wissenschaftler Flüge unter Verwendung von Parametern, die aus tatsächlichen Gleitbeobachtungen realer Drachen erhalten wurden (der Vergleich von Simulationen und Beobachtungen ist im Bild unten dargestellt).

Bild Nr. 3 Im
Vergleich dazu funktioniert das Modell, weist jedoch einige geringfügige Ungenauigkeiten auf, die in Zukunft behoben werden müssen.
Um den Einfluss der Welligkeit auf die Planungsmerkmale zu testen, wurden zwei Simulationen durchgeführt: mit f θ = 0 Hz (ohne Welligkeit) und f θ= 1,2 Hz (durchschnittliche Wellenfrequenz bei Schlangen). In beiden Fällen ist & ngr; θ und θ m wurden variiert ( 4a ).

Bild №4 Die
kinematischen Daten der Schlangenkörperform im Modell ermöglichten es, 121 Formen mit 1 ≤ ν θ ≤ 1,5 Körperwellen und horizontalen Wellenamplituden im Bereich von 90 ° ≤ θ m ≤ 119 ° zu erhalten. Ferner wurden die beobachteten Körperformen aus dieser Anordnung extrahiert (mittlerer Teil des Graphen, entlang der Diagonale getrennt; 4b ). Der hervorgehobene Teil des Diagramms enthält „offene“ Körperformen (ähnlich dem Buchstaben S), und der obere Teil ist „geschlossen“ (ähnlich einem Unendlichkeitszeichen).
Die vertikale Wellenamplitude und der dorsoventrale Winkel wurden auf einem konstanten Niveau gehalten: 20 ° bzw. 10 °. Die Simulation wurde als abgeschlossen angesehen, wenn der Massenschwerpunkt der Schlange den Boden berührte (Landung) oder wenn einer der Orientierungswinkel die 85 ° -Schwelle überschritt. Wenn dies geschah, wurde die Planung als instabil angesehen, d.h. nicht das gleiche wie in der Natur. Während der Simulation wurden sowohl die Kurzzeitdynamik (Starthöhe 10 m) als auch die Langzeitdynamik (Starthöhe 75 m) mit / ohne Welligkeit getestet.
Das Modell zeigt, dass sich Wellen positiv auf die Gleitleistung auswirken und typischerweise die horizontalen und vertikalen Entfernungen vergrößern, die zurückgelegt werden, bevor der simulierte Drachen instabil wird.
Simulation einer fliegenden Schlange, die mit und ohne Welligkeit gleitet.
Eine kurze Planung mit einer Starthöhe von 10 m zeigte einen guten Stabilitätskoeffizienten bei Welligkeit (94%). Wenn die Welligkeit nicht im Modell enthalten war, waren nur 50% der Flüge stabil. Die Welligkeit erhöht auch die Gleitstrecke (von 4 m auf 4,3 m).
Bei der Simulation des Gleitens aus 75 m vergrößerte die Welligkeit sowohl den horizontalen als auch den vertikalen Abstand, bevor sich bei 86% der Starts eine Instabilität zeigte. In diesem Fall erhöhte die Welligkeit bei 92% der Starts auch die Flugentfernung. Die Welligkeit erhöhte auch den durchschnittlichen horizontalen Abstand um 6,9 m.
Um den Einfluss der Amplitude der vertikalen Welle und der dorsoventralen Biegung auf die Gleitdynamik zu klären, wurden bei der Modellierung unterschiedliche Werte dieser Parameter verwendet und die Ergebnisse berücksichtigt.
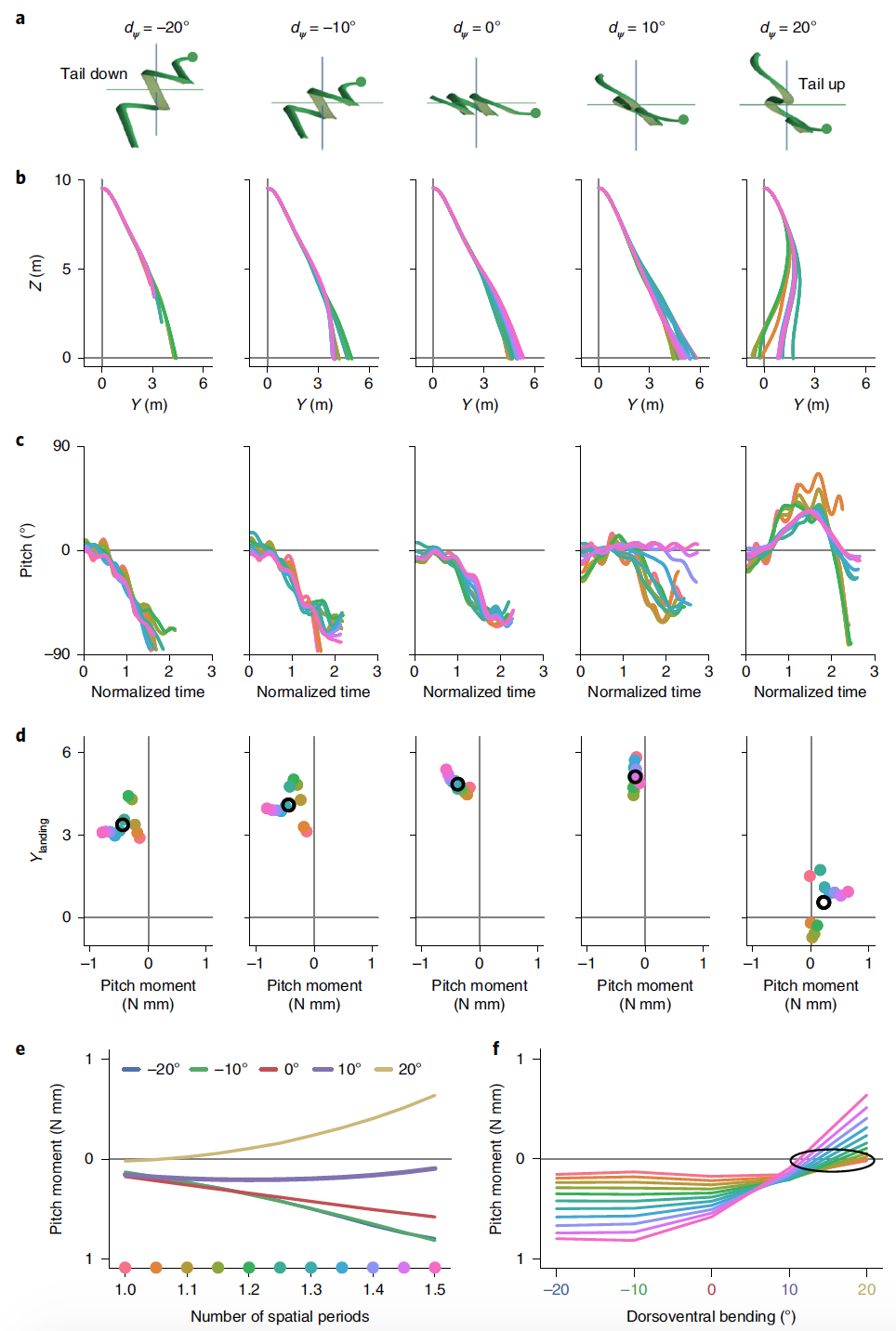
Bild Nr. 5 Die
Planung wurde mit ψ m = 0 °, 10 ° und 20 ° und einer dorsoventralen Biegung von -20 ° bis 20 ° in Schritten von 10 ° ( 5a ) für 11 verschiedene Körperformen simuliert.
Vertikale Schwingungen haben relativ geringe Auswirkungen auf die Gleitbahn, während die dorsoventrale Biegung einen signifikanten Einfluss hat.
Eine vollkommen flache Schlange (ψ m= 0 °), der bei experimentellen Tests nie beobachtet wurde, zeigte die erwarteten schlechtesten Ergebnisse. Durch Erhöhen der Amplitude der vertikalen Welle wurde die Planungseffizienz aufgrund der Verdrehung des Querschnitts in der Ebene erhöht, wodurch ein günstigerer Winkel für die Erzeugung der Kraft ( 2j ) bereitgestellt wurde .
Im Gegensatz zur vertikalen Wellenamplitude hatte die dorsoventrale Biegung einen spürbaren Einfluss auf die Gleiteigenschaften, insbesondere auf die Tonhöhe.
Bei ψ m = –20 ° mit der Rückseite des Körpers unter dem Kopf war die Planung nicht flach, sondern wurde in der Höhe instabil, bevor sie um 10 m fiel. Bei ψ m= 20 ° mit der Rückseite des Körpers über dem Kopf, die Flugbahn ist nach hinten gekrümmt, wobei einige Körperformen hinter dem Sprung landen. Eine solche schlechte Planung ist gerechtfertigt, indem der Körper nach oben gekippt wird. Trotzdem hatten Segelflugzeuge mit den oben genannten Parametern eine gute Rotationsstabilität.
Um die Verbindung zwischen der dorsoventralen Körperbiegung, der Neigung und den Planungsmerkmalen zu überprüfen, wurde eine Simulation ohne Rotation durchgeführt. Anstatt das gekoppelte nichtlineare Gleichungssystem Nr. 4 und Nr. 5 zu lösen, untersuchten die Wissenschaftler die aerodynamischen Kräfte in verschiedenen Phasen des Körpers während des Wellenzyklus. Ferner wurde hier Gleichung Nr. 4 integriert und die Position und Geschwindigkeit des Massenschwerpunkts berechnet.
Im Wesentlichen handelt es sich bei dieser Manipulation um ein "virtuelles Windkanal" -Experiment, bei dem ein dynamisches Modell verwendet wird, um die verteilten Kräfte zu berechnen, die auf einen Körper wirken, wenn dieser beschleunigt. Mit dieser Methode können Sie die Beziehung zwischen Translations- und Rotationsbewegung beseitigen, um einzelne aerodynamische und Trägheitsbeiträge zur Rotationsbewegung zu quantifizieren.
Mit einer Zunahme der dorsoventralen Biegung von -20 ° auf 10 ° nimmt die Landeposition der simulierten Schlange zu, wenn die durchschnittliche Neigung in Richtung Null zunimmt ( 5d ). Bei einer dorsoventralen Biegung von 20 ° wird das phasengemittelte Nickmoment positiv und die Gleitleistung nimmt ab.
Für jeden dorsoventralen Biegewinkel hängen die Planungseffizienz und das mittlere schräge Moment auch von der verwendeten Form ab, insbesondere von der Anzahl der räumlichen Perioden und der Amplitude der horizontalen Welle. Für jede Körperform zum Zeitpunkt der Planung hat die dorsoventrale Biegung einen großen Einfluss auf das durchschnittliche Nickmoment, und mit zunehmender Anzahl von Raumperioden divergieren die Momente und werden je nach d ψ positiver oder negativer .
Die Markierungen der phasengemittelten Nickmomente bei 5e entsprechen der bei 5c gezeigten Steigung oder Steigung und der resultierenden Gleitleistung bei 5b . Bei 5fEs wird gezeigt, dass für Körperformen mit der kleinsten räumlichen Periode das durchschnittliche Nickmoment das kleinste ist.
Aus den oben beschriebenen Daten kann angenommen werden, dass die vertikale Welle bewirkt, dass der Körper aus der Ebene rollt und die lokale Ausrichtung des "abgeflachten Flügels" (die Form des Körpers der Schlange während des Gleitens) mit Hilfe des Luftstroms ändert. Die dorsoventrale Biegung steuert die Größe und das Vorzeichen des aerodynamischen Impulses, der den Körper beeinflusst. Ein fliegender Drachen kann das Nickmoment steuern, indem er den Biegewinkel des dorsoventralen Bereichs oder die Form einer horizontalen Welle während des Fluges ändert.
Folglich spielt die dorsoventrale Krümmung des Körpers eine äußerst wichtige Rolle für die Gleitstabilität, eine erfolgreiche Landung und die Fähigkeit, die Gleitbahn direkt während ihrer Ausführung zu ändern.

Bild Nr. 6
Die Phasenanalyse durch Mittelung ermöglicht es, den relativen Beitrag von aerodynamischen und Trägheitsmomenten zur Gleitdynamik zu quantifizieren.
Aus den Gleichungen Nr. 5 folgt, dass sowohl die aerodynamischen Kräfte als auch die sich ändernde Massenverteilung die Orientierung des Körpers beeinflussen. Der aerodynamische Beitrag ( 6a ) nimmt mit zunehmender Geschwindigkeit mit der Zeit zu, während der Trägheitsbeitrag ( 6b ) konstant bleibt. Beide Momente sind periodisch und nur das Tonhöhenmoment zeigt einen Phasendurchschnitt ungleich Null.
Anfangs überwiegen Trägheitsmomente in der Nähe der Nick- und Rollachse, aber während eines wellenartigen Zyklus nimmt ihr Beitrag schnell ab. Die Trägheitsmomente des Gierens sind in der Regel eine Größenordnung größer als die aerodynamischen Momente des Gierens und größer als die Trägheitsmomente um andere Achsen. Trägheitsmomente des Gierens entstehen aufgrund einer horizontalen Welle mit großer Amplitude und eines breiten S-förmigen Körpers. Dieses Ergebnis legt nahe, dass Drachen die Trägheitsrotation als Manövriermechanismus verwenden können.
Um die Nuancen der Studie genauer kennenzulernen, empfehle ich Ihnen, den Bericht von Wissenschaftlern und zusätzliche Materialien zu lesen.
Und wer sich mit der Software vertraut machen möchte, mit der die Planung eines fliegenden Drachens analysiert wird, kann diesem Link folgen .
Epilog
In dieser Studie verwendeten die Wissenschaftler die neuesten Techniken zur Bewegungserfassung und 3D-Modellierung, um ein anatomisch genaues Modell einer fliegenden Schlange zu erstellen.
Früher war es auch schwierig, die Dynamik eines Vogelfluges zu verstehen, aber es verwirrte die Wissenschaftler nicht so sehr wie ein fliegender Drachen. In der Natur gibt es nicht viele Beispiele für flügellose Flüge, und alle sind mit der Verwendung von nicht standardmäßigen Mechanismen verbunden, die es dem Tier ermöglichen, zu planen und nicht mit einem Stein zu Boden zu fallen.
Bei fliegenden Schlangen spielt die Welligkeit, die bei der Bewegung von kriechenden und schwimmenden Schlangen beobachtet wird, eine sehr wichtige Rolle. Ein zusätzlicher Mechanismus zur Stabilisierung der Planung ist die Korrektur des dorsoventralen Winkels der Körperbeugung. Durch die Kombination dieser Elemente können fliegende Drachen von Baum zu Baum fliegen und wissen genau, wo sie später gepflanzt werden.
Die Autoren dieser Arbeit glauben, dass ihre Daten es uns nicht nur ermöglichten, die Gewohnheiten geschmückter Baumschlangen besser zu verstehen, sondern auch zusätzliche Inspiration für die Entwicklung schlangenartiger Roboter zu erhalten. Ja, solche Roboter gibt es bereits. Sie kriechen, können auf schwierigen Oberflächen navigieren und schwer zugängliche Stellen erreichen, aber können sie fliegen?
Mit solchen Überlegungen wird unsere Welt bald der Stadt der Maschinen aus der "Matrix" ähneln, in der äußerst ungewöhnliche (und leicht beängstigende) Roboterkreaturen an den Wänden entlang krochen, deren Zweck schwer zu verstehen war. Der Wunsch eines Menschen, eine Roboterversion von allem, was ihn umgibt, herzustellen, kann nicht betrogen werden. Dies ist unsere Natur - alles zu verstehen, alles zu wissen, in der Lage zu sein, das zu erschaffen, was die Natur schön vor uns getan hat. Wenn Roboterschlangen, Spinnen, Hunde und andere Robotertiere viel mehr Nutzen als Schaden bringen, ist eine solche Forschung völlig gerechtfertigt.
Vielen Dank für Ihre Aufmerksamkeit, bleiben Sie neugierig und haben Sie ein tolles Wochenende Jungs!
Freitag off-top:
, .
, .
Off-Top 2.0:
, :)
, :)
Ein bisschen Werbung
Vielen Dank für Ihren Aufenthalt bei uns. Gefällt dir unser Artikel? Möchten Sie weitere interessante Inhalte sehen? Unterstützen Sie uns, indem Sie eine Bestellung aufgeben oder Freunden Cloud-VPS für Entwickler ab 4,99 US-Dollar empfehlen , ein einzigartiges Analogon von Einstiegsservern, das wir für Sie erfunden haben: Die ganze Wahrheit über VPS (KVM) E5-2697 v3 (6 Kerne) 10 GB DDR4 480 GB SSD 1 Gbit / s ab 19 $ oder wie teilt man den Server? (Optionen sind mit RAID1 und RAID10, bis zu 24 Kernen und bis zu 40 GB DDR4 verfügbar).
Dell R730xd ist im Equinix Tier IV-Rechenzentrum in Amsterdam 2x billiger? Nur wir haben 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2,6 GHz 14C 64 GB DDR4 4 x 960 GB SSD 1 Gbit / s 100 TV von 199 US-Dollar in den Niederlanden!Dell R420 - 2x E5-2430 2,2 GHz 6C 128 GB DDR3 2x960 GB SSD 1 Gbit / s 100 TB - ab 99 US-Dollar! Lesen Sie mehr über den Aufbau eines Infrastrukturgebäudes. Klasse mit Dell R730xd E5-2650 v4 Servern für 9.000 Euro pro Penny?