Im vorherigen Teil haben wir bei der Tatsache angehalten, dass es notwendig ist, die Farbe eines Pixels aus der ursprünglichen Rasterkarte durch geodätische Koordinaten (Breite,
Länge) zu erhalten, die bereits in den SC dieser Karte übersetzt wurden.
Geodätische Koordinaten werden auf der Oberfläche des Ellipsoids und Pixelkoordinaten in der Ebene eingestellt, d.h. Sie brauchen einen Weg, um von einer konvexen zu einer flachen Oberfläche zu gelangen. Das Problem ist, dass eine konvexe Oberfläche (stellen Sie sich vor, dass eine Art Zeichnung oder ein Koordinatengitter darauf angewendet wird) nicht ohne Verzerrung auf eine flache Oberfläche übertragen werden kann. Kann verzerrt sein: Form (Winkel), Fläche, lineare Abmessungen. Es besteht natürlich die Möglichkeit und nicht die einzige, auf eine flache Oberfläche zu übertragen, ohne nur eines zu verzerren, aber der Rest wird unweigerlich verzerrt.

Offensichtlich sind Verzerrungen auf kleineren Skalen (dem gesamten Planeten, Kontinent) stärker ausgeprägt als auf größeren (Region, Stadt), und auf der größten (Plan eines kleinen Gebiets) sprechen wir überhaupt nicht darüber, weil Die Oberfläche des Ellipsoids auf solchen Skalen ist nicht mehr von der Ebene zu unterscheiden.
Hier kommen wir zum Konzept der Kartenprojektion. Ich werde keine Beispiele mit Bildern der Projektion einer Kugel auf einen Zylinder oder einen Kegel mit anschließender Entwicklung geben, für uns ist es jetzt wichtig, zu verallgemeinern.
Eine Kartenprojektion ist eine mathematisch definierte Methode, um die Oberfläche eines Ellipsoids auf eine Ebene abzubilden. Einfach ausgedrückt sind dies mathematische Formeln zur Umwandlung geodätischer Koordinaten (Breite, Länge) in flache kartesische Koordinaten - genau das, was wir brauchen.
Es wurde eine Vielzahl von kartografischen Projektionen erfunden, die alle für ihre eigenen Zwecke Anwendung finden: gleich groß (in dem das Gebiet erhalten bleibt) für politische Karten, Bodenkarten, konform (in denen die Form erhalten bleibt) - für die Navigation, äquidistant (wobei der Maßstab in der gewählten Richtung beibehalten wird) - für Computer Verarbeitung und Speicherung von Geodaten-Arrays. Es gibt auch Projektionen, die die oben genannten Merkmale in bestimmten Proportionen kombinieren, es gibt vollständig esoterische Projektionen. Beispiele für Projektionen finden Sie auf Wikipedia auf der Seite Liste der Kartenprojektionen.
Für jede Projektion werden entweder exakte Formeln abgeleitet oder in Form einer Summe unendlicher konvergierender Reihen, und im letzteren Fall kann es sogar mehrere Optionen geben. Die Projektionsformeln wandeln Breiten- und Längengrade in kartesische Koordinaten um. In solchen Koordinaten wird normalerweise der Zähler als Maßeinheit verwendet. Ein solches 1-Meter-Rechteckgitter kann manchmal auf einer Karte (in Form eines Kilometergitters) aufgezeichnet werden, wird jedoch in den meisten Fällen nicht aufgezeichnet. Aber wir wissen jetzt, dass es immer noch in impliziter Form existiert. Der auf der Karte angegebene Maßstab der Karte wird nur relativ zur Größe dieses Rasters berechnet. Es versteht sich von selbst, dass 1 Meter auf einem solchen Koordinatengitter 1 Meter auf dem Boden entspricht, nicht auf der gesamten Karte, sondern nur an einigen Punkten entlang einer bestimmten Linie oder entlang Linien in einer bestimmten Richtung.in anderen Punkten oder Richtungen treten Verzerrungen auf und 1 Meter am Boden entspricht nicht 1 Meter des Koordinatengitters.
Ein kleiner Exkurs. Die Funktion aus dem ersten Teil des Artikels WGS84_XYZ ist genau die Transformation von Koordinaten aus dem WGS84 SC in rechteckige Koordinaten, jedoch nicht in Metern, sondern in Pixeln. Wie Sie sehen können, ist die Formel dort äußerst einfach. Wenn die Mercator-Projektion nicht auf einer Kugel, sondern auf einem Ellipsoid verwendet würde, wäre die Formel komplizierter. Aus diesem Grund wurde eine Kugel ausgewählt, um den Browsern das Leben zu erleichtern. Später hat die WebMercator-Projektion mit ihrer Kugel Wurzeln geschlagen, für die sie häufig kritisiert wird.
Für meine Bedürfnisse habe ich ein Dokument namens "Kartenprojektionen des US Geological Survey" im PDF-Format verwendet, das im Internet verfügbar ist. Das Dokument enthält detaillierte Anweisungen für jede Projektion, um das Schreiben einer Transformationsfunktion in einer Programmiersprache zu vereinfachen.
Schreiben wir weiter unseren Algorithmus. Lassen Sie uns eine der beliebten Projektionen namens Transverse Mercator und eine ihrer Varianten namens Gauss-Kruger-Projektion implementieren.
struct TransverseMercatorParam {
struct Ellipsoid *ep;
double k; /* */
double lat0; /* ( ) */
double lon0; /* ( ) */
double n0; /* */
double e0; /* */
double zw; /* ( ) */
double zs; /* */
//
double e2__a2k2, ie2__a2k2, m0, mp, imp;
double f0, f2, f4, f6;
double m1, m2, m4, m6;
double q, q1, q2, q3, q4, q6, q7, q8;
double q11, q12, q13, q14, q15, q16, q17, q18;
// - 2
double apk, n, b, c, d;
double b1, b2, b3, b4;
};
struct TransverseMercatorParam TM_GaussKruger = {
.ep = &Ellipsoid_Krasovsky,
.zw = rad(6,0,0),
.lon0 = -rad(3,0,0),
.e0 = 5e5,
.zs = 1e6,
};
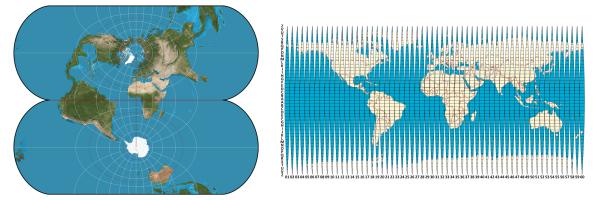
Ein Merkmal der transversalen Mercator-Projektion ist, dass sie konform ist, dh die Form von Objekten auf der Karte und die Winkel bleiben erhalten, sowie die Tatsache, dass der Maßstab entlang eines Mittelmeridians erhalten bleibt. Die Projektion ist für den gesamten Globus geeignet, aber die Verzerrungen nehmen mit der Entfernung vom Mittelmeridian zu, sodass die gesamte Erdoberfläche entlang der Meridiane, die als Zonen bezeichnet werden, in schmale Streifen geschnitten wird, für die jeweils ein eigener Mittelmeridian verwendet wird. Beispiele für die Implementierung solcher Projektionen sind die Gauß-Kruger-Projektion und UTM, bei denen auch das Verfahren zur Verteilung von Koordinaten über Zonen definiert ist, d.h. definiert und gleichnamig SC.
Und in der Tat der Code der Funktionen der Initialisierung und Transformation von Koordinaten. In der Initialisierungsfunktion werden Konstanten einmalig berechnet, die von der Konvertierungsfunktion wiederverwendet werden.
void setupTransverseMercator(struct TransverseMercatorParam *pp) {
double sin_lat, cos_lat, cos2_lat;
double q, n, rk, ak;
if (!pp->k)
pp->k = 1.0;
sin_lat = sin(pp->lat0);
cos_lat = cos(pp->lat0);
cos2_lat = cos_lat * cos_lat;
q = pp->ep->e2 / (1 - pp->ep->e2);
// n = (a-b)/(a+b)
n = (pp->ep->a - pp->ep->b) / (pp->ep->a + pp->ep->b);
rk = (pp->ep->a + pp->ep->b) * pp->k / 2;
ak = pp->ep->a * pp->k;
pp->e2__a2k2 = pp->ep->e2 / (ak * ak);
pp->ie2__a2k2 = (1 - pp->ep->e2) / (ak * ak);
pp->f6 = 1097.0/4 * n*n*n*n;
pp->f4 = (151.0/3 - 3291.0/8 * n) * n*n*n;
pp->f2 = (21.0/2 + (-151.0/3 + 5045.0/32 * n) * n) * n*n;
pp->f0 = (3.0 + (-21.0/4 + (31.0/4 - 657.0/64 * n) * n) * n) * n;
pp->m6 = rk * 315.0/4 * n*n*n*n;
pp->m4 = rk * (-70.0/3 - 945.0/8 * n) * n*n*n;
pp->m2 = rk * (15.0/2 + (70.0/3 + 1515.0/32 * n) * n) * n*n;
pp->m1 = rk * (-3.0 + (-15.0/4 + (-4.0 - 255.0/64 * n) * n) * n) * n;
// polar distance
pp->mp = rk * (1.0 + (1.0/4 + 1.0/64 * n*n) * n*n);
pp->imp = 1 / pp->mp;
pp->m0 = pp->n0 - pp->mp * pp->lat0 - sin_lat * cos_lat *
(pp->m1 + (pp->m2 + (pp->m4 + pp->m6 * cos2_lat) * cos2_lat) * cos2_lat);
pp->q = q;
pp->q1 = 1.0/6 * q*q;
pp->q2 = 3.0/8 * q;
pp->q3 = 5.0/6 * q;
pp->q4 = 1.0/6 - 11.0/24 * q;
pp->q6 = 1.0/6 * q;
pp->q7 = 3.0/5 * q;
pp->q8 = 1.0/5 - 29.0/60 * q;
pp->q11 = - 5.0/12 * q;
pp->q12 = -5.0/24 + 3.0/8 * q;
pp->q13 = - 1.0/240 * q*q;
pp->q14 = 149.0/360 * q;
pp->q15 = 61.0/720 - 63.0/180 * q;
pp->q16 = - 1.0/40 * q*q;
pp->q17 = - 1.0/60 * q;
pp->q18 = 1.0/24 + 1.0/15 * q;
// - 2
double e2 = pp->ep->e2;
pp->apk = ak * (1 + n*n / 4 + n*n*n*n / 64) / (1 + n);
pp->n = n;
pp->b = (5 - e2) * e2 * e2 / 6;
pp->c = (104 - 45 * e2) * e2 * e2 * e2 / 120;
pp->d = 1237.0/1260 * e2 * e2 * e2 * e2;
pp->b1 = (1.0/2 + (-2.0/3 + (5.0/16 + 41.0/180 * n) * n) * n) * n;
pp->b2 = (13.0/48 + (-3.0/5 + 557.0/1440 * n) * n) * n*n;
pp->b3 = (61.0/240 - 103.0/140 * n) * n*n*n;
pp->b3 = 49561.0/161280 * n*n*n*n;
}
void translateTransverseMercator(struct TransverseMercatorParam *pp, int zone,
double lat, double lon, double *ep, double *np) {
double lon2, v, m;
double k4, k6, h3, h5;
double sin_lat = sin(lat);
double cos_lat = cos(lat);
double cos2_lat = cos_lat * cos_lat;
lon -= zone * pp->zw + pp->lon0;
while (unlikely(lon <= -M_PI))
lon += 2*M_PI;
lon2 = lon * lon;
//
v = 1 / sqrt(pp->e2__a2k2 * cos2_lat + pp->ie2__a2k2);
m = ((pp->m6 * cos2_lat + pp->m4) * cos2_lat + pp->m2) * cos2_lat + pp->m1;
k4 = ((pp->q1 * cos2_lat + pp->q2) * cos2_lat + 1.0/4 ) * cos2_lat - 1.0/24;
k6 = ((pp->q3 * cos2_lat + pp->q4) * cos2_lat - 1.0/12) * cos2_lat + 1.0/720;
h3 = (( pp->q6) * cos2_lat + 1.0/3 ) * cos2_lat - 1.0/6;
h5 = ((pp->q7 * cos2_lat + pp->q8) * cos2_lat - 1.0/6 ) * cos2_lat + 1.0/120;
// ( )
*np = pp->m0 + pp->mp * lat
+ (m + v * ((k6 * lon2 + k4) * lon2 + 0.5) * lon2) * cos_lat * sin_lat;
*ep = pp->e0 + pp->zs * zone
+ ( v * ((h5 * lon2 + h3) * lon2 + 1.0) * lon ) * cos_lat;
}
Am Ausgang der Transformationsfunktion haben wir Koordinaten: Ost- und Nordverschiebung (e, n) sind rechteckige kartesische Koordinaten in Metern.

Wir sind bereits sehr nahe daran, unseren Algorithmus zu vervollständigen. Wir müssen nur die Koordinaten des Pixels (x, y) in der Kartendatei finden. weil Pixelkoordinaten sind ebenfalls kartesisch, dann können wir sie durch affine Transformation (e, n) zu (x, y) finden. Wir werden etwas später auf die Parameter der affinsten Transformation zurückkommen.
struct AffineParam {
double c00, c01, c02;
double c10, c11, c12;
};
void translateAffine(struct AffineParam *app, double e, double n,
double *xp, double *yp) {
*xp = app->c00 + app->c01 * e + app->c02 * n;
*yp = app->c10 + app->c11 * e + app->c12 * n;
}
Und schließlich der vollständige Algorithmus zur Kachelerstellung:
void renderTile(ImagePtr tile, int z, unsigned long x, unsigned long y) {
int i, j;
double wlat, wlon;
ImagePtr srcimg;
double lat, lon;
double e, n;
double x, y;
for (i = 0; i < 256; ++i) {
for (j = 0; j < 256; ++j) {
XYZ_WGS84(x * 256 + j, y * 256 + i, z, &wlat, &wlon);
translateHelmertInv(&Helmert_SK42_WGS84, wlat, wlon, 0, &lat, &lon);
findSrcImg(&srcimg, lat, lon);
translateTransverseMercator(&TM_GaussKruger, srcimg->zone, lat, lon, &e, &n);
translateAffine(&srcimg->affine, e, n, &x, &y);
setPixelColor(tile, j, i, interpolatePixelColor(srcimg, x, y));
}
}
}
Das Ergebnis der Arbeit für z = 12, y = 1377, x = 2391:

Im Algorithmus wurde die Funktion des Findens des Originalbildes der srcimg-Karte aus den im SC der Karte angegebenen geodätischen Koordinaten lat, lon nicht beschrieben. Ich denke, es wird keine Probleme damit und mit der Nummer der srcimg-> Zone geben, aber wir werden näher darauf eingehen, die Parameter der affinen Transformation srcimg-> affine genauer zu finden.
Irgendwo im Internet wurde vor sehr langer Zeit eine solche Funktion gefunden, um die Parameter einer affinen Transformation zu finden. Ich zitiere sie sogar mit ursprünglichen Kommentaren:
struct TiePoint {
struct TiePoint *next;
double lon, lat;
double e, n;
double x, y;
};
void setupAffine(struct AffineParam *app, struct TiePoint *plist) {
/*
* :
* x = c00 + c01 * e + c02 * n
* y = c10 + c11 * e + c12 * n
*/
struct TiePoint *pp; /* */
double a11, a12, a13; /* */
double a21, a22, a23; /* 3*3 */
double a31, a32, a33; /* */
double b1, b2, b3; /* */
int m; /* z: m=0 -> z=x, m=1 -> z=y */
double z; /* x, y */
double t; /* */
/* 2- 3 ,
. */
/* */
a11 = a12 = a13 = a22 = a23 = a33 = 0;
for (pp = plist; pp; pp = pp->next) {
a11 += 1;
a12 += pp->e;
a13 += pp->n;
a22 += pp->e * pp->e;
a23 += pp->e * pp->n;
a33 += pp->n * pp->n;
}
/* ( ) */
a21 = a12;
a31 = a13;
a12 /= a11;
a13 /= a11;
a22 -= a21 * a12;
a32 = a23 - a31 * a12;
a23 = a32 / a22;
a33 -= a31 * a13 + a32 * a23;
/* , X Y */
for (m = 0; m < 2; m++) { /* m=0 -> X, m=1 -> Y */
/* */
b1 = b2 = b3 = 0;
for (pp = plist; pp; pp = pp->next) {
z = !m ? pp->x : pp->y;
b1 += z;
b2 += pp->e * z;
b3 += pp->n * z;
}
/* */
b1 /= a11;
b2 = (b2 - a21 * b1) / a22;
b3 = (b3 - a31 * b1 - a32 * b2) / a33;
/* */
t = b2 - a23 * b3;
*(!m ? &app->c00 : &app->c10) = b1 - a12 * t - a13 * b3;
*(!m ? &app->c01 : &app->c11) = t;
*(!m ? &app->c02 : &app->c12) = b3;
}
}
Bei der Eingabe müssen mindestens drei Ankerpunkte übermittelt werden, bei der Ausgabe erhalten wir vorgefertigte Parameter. Ankerpunkte sind Punkte, für die sowohl die Pixelkoordinaten (x, y) als auch die Ost- und Nordversatzkoordinaten (e, n) bekannt sind. Die Schnittpunkte des Kilometergitters auf der Originalkarte können als solche Punkte verwendet werden. Was ist, wenn auf der Karte kein Kilometerraster vorhanden ist? Dann können Sie die Paare (x, y) und (lon, lat) festlegen, da solche Punkte die Schnittpunkte der Parallelen und Meridiane nehmen und sich immer auf der Karte befinden. Es bleibt nur die Konvertierung (lon, lat) in (e, n), dies erfolgt durch die Transformationsfunktion für die Projektion, in unserem Fall translateTransverseMercator ().
Wie Sie sehen können, werden die Ankerpunkte benötigt, um dem Algorithmus mitzuteilen, welchen Teil der Erdoberfläche die Datei mit dem Kartenbild beschreibt. Da beide Koordinatensysteme kartesisch waren, unabhängig davon, wie viele Ankerpunkte wir setzen und wie weit sie voneinander entfernt sind, liegt die Diskrepanz über die gesamte Kartenebene innerhalb des Fehlers bei der Bestimmung der Ankerpunkte. Die meisten Fehler bestehen darin, dass die falsche (mit nicht genau festgelegten Parametern) Projektion, Datum oder Ellipsoid verwendet wird. Infolgedessen befinden sich die Koordinaten (e, n) am Ausgang nicht im kartesischen Koordinatensystem, sondern in einer relativ zum kartesischen leicht gekrümmten. Optisch kann dies als „zerknittertes Blatt“ dargestellt werden. Eine Erhöhung der Anzahl der Ankerpunkte löst dieses Problem natürlich nicht. Das Problem kann gelöst werden, indem die Parameter der Projektion, des Bezugspunkts und des Ellipsoids eingestellt werden.In diesem Fall können Sie mit einer großen Anzahl von Ankerpunkten das „Blatt“ genauer glätten und die ungeglätteten Bereiche nicht übersehen.
Und am Ende des Artikels werde ich Ihnen erklären, wie Sie vorgefertigte Kacheln in OpenLayers verwenden und in welcher Form Sie sie für das OsmAnd-Programm vorbereiten.
Für OpenLayers müssen Sie nur die Kacheln im Web platzieren und benennen, damit Sie (z, y, x) im Datei- oder Verzeichnisnamen
hervorheben können , zum Beispiel: /tiles/topo/12_1377_2391.jpg
oder noch besser:
/ tiles / topo /12/1377/2391.jpg
Dann können Sie sie folgendermaßen verwenden:
map = new OpenLayers.Map (...);
map.addLayer(new OpenLayers.Layer.XYZ("Topo Maps", "/tiles/topo/${z}_${y}_${x}.jpg", {
isBaseLayer: false, visibility: false,
}));
Für das OsmAnd-Programm ist es einfach, das Format aus vorhandenen Dateien mit einer Reihe von Kacheln zu bestimmen. Ich werde Ihnen sofort über die Ergebnisse berichten. Die Kacheln werden in eine SQLite-Datenbankdatei gepackt, die wie folgt erstellt wird:
CREATE TABLE info AS SELECT 99 AS minzoom, 0 AS maxzoom;
CREATE TABLE tiles (x int, y int, z int, s int, image blob, PRIMARY KEY (x,y,z,s));
CREATE INDEX IND on tiles (x,y,z,s);
UPDATE info SET minzoom=$minzoom, maxzoom=$maxzoom
Die Spalte s ist immer mit Null gefüllt, wofür ich nicht verstanden habe, dass das Bild in der ursprünglichen Binärform eingegeben wird, das Format (jpg, png, gif) verloren geht, aber OsmAnd es anhand seines Inhalts bestimmt. Kacheln in verschiedenen Formaten können in eine Datenbank gepackt werden. Anstelle von $ minzoom und $ maxzoom müssen die Skalierungsgrenzen der in die Basis eingegebenen Kacheln ersetzt werden. Die fertige Datenbankdatei, z. B. Topo.sqlitedb, wird auf ein Smartphone oder Tablet im Verzeichnis osmand / tiles übertragen. Starten Sie OsmAnd neu. Im Menü -> "Karte konfigurieren" -> "Obere Ebene" wird eine neue Option "Topo" angezeigt. Dies ist eine Karte mit unseren neuen Kacheln.