Buch "Verarbeitung natürlicher Sprache in Aktion"

Hallo Bewohner! Wir haben einen praktischen Leitfaden zur Verarbeitung und Erstellung von Texten in natürlicher Sprache veröffentlicht. Das Buch ist mit allen Tools und Techniken ausgestattet, die zum Erstellen angewandter NLP-Systeme erforderlich sind, um den Betrieb eines virtuellen Assistenten (Chatbot), eines Spamfilters, eines Forumsmoderatorprogramms, eines Stimmungsanalysators, eines Programms zum Aufbau von Wissensdatenbanken, eines intelligenten Textanalysators in natürlicher Sprache oder eines zu gewährleisten So gut wie jede andere NLP-Anwendung, die Sie sich vorstellen können.



Das Buch richtet sich an fortgeschrittene Python-Entwickler. Ein wesentlicher Teil des Buches wird für diejenigen Leser nützlich sein, die bereits wissen, wie man komplexe Systeme entwirft und entwickelt, da es zahlreiche Beispiele für empfohlene Lösungen enthält und die Fähigkeiten der modernsten NLP-Algorithmen aufzeigt. Kenntnisse in der objektorientierten Programmierung in Python können Ihnen zwar beim Aufbau besserer Systeme helfen, die Informationen in diesem Buch müssen jedoch nicht verwendet werden.

Neuronale Rückkopplungsnetze: wiederkehrende neuronale Netze

Kapitel 7 zeigt die Möglichkeiten, ein Fragment oder einen ganzen Satz mithilfe eines Faltungsnetzwerks zu analysieren und benachbarte Wörter in einem Satz zu verfolgen, indem ein Filter für gemeinsame Gewichte (Faltung) auf sie angewendet wird. Wörter, die in Gruppen vorkommen, können auch in einem Bündel gefunden werden. Das Web ist auch resistent gegen kleine Verschiebungen in den Positionen dieser Wörter. Gleichzeitig können benachbarte Konzepte das Netzwerk erheblich beeinflussen. Aber wenn Sie einen Blick auf das Gesamtbild des Geschehens werfen müssen, berücksichtigen Sie die Beziehungen über einen längeren Zeitraum, ein Fenster, das mehr als 3-4 Token aus dem Vorrat abdeckt? Wie kann das Konzept vergangener Ereignisse in das Netzwerk eingeführt werden? Erinnerung?



Für jedes Trainingsbeispiel (oder jede Reihe von ungeordneten Beispielen) und jede Ausgabe (oder jede Reihe von Ausgaben) des neuronalen Feed-Forward-Netzwerks müssen die Gewichte des neuronalen Netzwerks für einzelne Neuronen basierend auf der Backpropagation-Methode angepasst werden. Das haben wir bereits gezeigt. Die Ergebnisse der Trainingsphase für das folgende Beispiel sind jedoch weitgehend unabhängig von der Reihenfolge der Eingabedaten. Faltungs-Neuronale Netze versuchen, diese Ordnungsbeziehungen durch Erfassung lokaler Beziehungen zu erfassen, aber es gibt einen anderen Weg.



In einem Faltungs-Neuronalen Netzwerk wird jedes Trainingsbeispiel als gruppierter Satz von Wort-Token an das Netzwerk übergeben. Die Wortvektoren sind in einer Matrix in der Form (Länge des Wortvektors × Anzahl der Wörter im Beispiel) gruppiert, wie in Fig. 1 gezeigt. 8.1.





Diese Folge von Wortvektoren kann jedoch genauso einfach aus Kapitel 5 (Abbildung 8.2) auf das normale neuronale Feedforward-Netzwerk übertragen werden, oder?





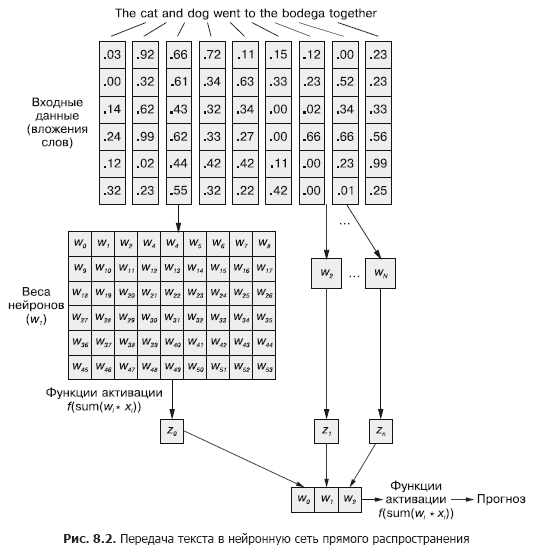
Dies ist natürlich ein perfekt funktionierendes Modell. Mit dieser Methode zur Weitergabe von Eingabedaten kann das neuronale Feedforward-Netzwerk auf das gemeinsame Auftreten von Token reagieren, was wir benötigen. Gleichzeitig reagiert es auf alle gemeinsamen Ereignisse auf die gleiche Weise, unabhängig davon, ob sie durch einen langen Text getrennt sind oder nebeneinander liegen. Darüber hinaus können vorwärtsgerichtete neuronale Netze wie CNNs Dokumente mit variabler Länge nur schlecht verarbeiten. Sie können Text am Ende des Dokuments nicht verarbeiten, wenn er die Breite des Webs überschreitet.



Vorwärtsgerichtete neuronale Netze eignen sich am besten zur Modellierung der Beziehung einer Datenprobe als Ganzes zu ihrer entsprechenden Bezeichnung. Wörter am Anfang und am Ende eines Satzes haben dieselbe Auswirkung auf das Ausgangssignal wie in der Mitte, obwohl es unwahrscheinlich ist, dass sie semantisch miteinander in Beziehung stehen.



Diese Einheitlichkeit (Einheitlichkeit des Einflusses) kann eindeutig Probleme verursachen, beispielsweise bei harten Negationstoken und Modifikatoren (Adjektive und Adverbien) wie "nein" oder "gut". In einem vorwärtsgerichteten neuronalen Netzwerk beeinflussen Negationswörter die Bedeutung aller Wörter in einem Satz, selbst wenn sie weit von dem Ort entfernt sind, den sie tatsächlich beeinflussen sollten.



Eindimensionale Faltungen sind eine Möglichkeit, diese Beziehungen zwischen Token zu lösen, indem mehrere Wörter über Fenster hinweg analysiert werden. Die in Kapitel 7 beschriebenen Downsampling-Schichten sind speziell für kleine Änderungen der Wortreihenfolge ausgelegt. In diesem Kapitel werden wir einen anderen Ansatz betrachten, der uns dabei hilft, den ersten Schritt in Richtung des Konzepts des neuronalen Netzwerkspeichers zu machen. Anstatt eine Sprache als großen Datenblock zu zerlegen, werden wir uns im Laufe der Zeit mit ihrer sequentiellen Bildung befassen, Token für Token.

8.1. Auswendiglernen in neuronalen Netzen

Natürlich sind Wörter in einem Satz selten völlig unabhängig voneinander; Ihr Auftreten wird durch das Auftreten anderer Wörter im Dokument beeinflusst oder beeinflusst. Zum Beispiel: Das gestohlene Auto raste in die Arena und das Clownauto raste in die Arena.



Sie können völlig unterschiedliche Eindrücke der beiden Sätze haben, wenn Sie bis zum Ende lesen. Die Konstruktion der Phrase in ihnen ist dieselbe: Adjektiv, Substantiv, Verb und Präpositionalphrase. Aber das Ersetzen des Adjektivs in ihnen verändert das Wesen dessen, was geschieht, aus der Sicht des Lesers radikal.



Wie kann man eine solche Beziehung simulieren? Wie kann man verstehen, dass Arena und sogar Geschwindigkeit leicht unterschiedliche Konnotationen haben können, wenn im Satz ein Adjektiv vor ihnen steht, das keine direkte Definition von einem von ihnen ist?



Wenn es eine Möglichkeit gäbe, sich daran zu erinnern, was einen Moment zuvor passiert ist (insbesondere daran, was in Schritt t in Schritt t + 1 passiert ist), wäre es möglich, Muster zu identifizieren, die entstehen, wenn bestimmte Token in einer Folge von Mustern erscheinen, die anderen Token zugeordnet sind. Wiederkehrende neuronale Netze (RNNs) ermöglichen es einem neuronalen Netz, die vergangenen Wörter einer Sequenz zu speichern.



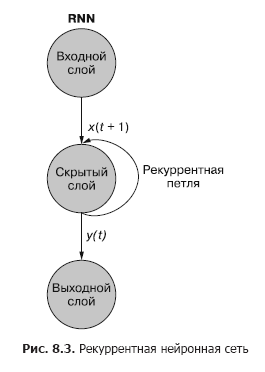
Wie Sie in Abb. In 8.3 fügt ein von der verborgenen Schicht getrenntes wiederkehrendes Neuron dem Netzwerk eine wiederkehrende Schleife hinzu, um die Ausgabe der verborgenen Schicht zum Zeitpunkt t "wiederzuverwenden". Die Ausgabe zum Zeitpunkt t wird zur nächsten Eingabe zum Zeitpunkt t + 1 addiert. Das Netzwerk verarbeitet diese neue Eingabe zum Zeitpunkt t + 1, um eine Ausgabe der verborgenen Schicht zum Zeitpunkt t + 1 zu erzeugen. Diese Ausgabe zum Zeitpunkt t + 1 dann wird es vom Netzwerk wiederverwendet und zu einem Zeitpunkt t + 2 usw. in das Eingangssignal aufgenommen.





Während die Idee, einen Zustand durch die Zeit zu beeinflussen, etwas verwirrend erscheint, ist das Grundkonzept einfach. Die Ergebnisse jedes Signals am Eingang eines herkömmlichen neuronalen Feedforward-Netzwerks zu einem Zeitpunkt t werden als zusätzliches Eingangssignal zusammen mit dem nächsten Datenelement verwendet, das dem Netzwerkeingang zu einem Zeitpunkt t + 1 zugeführt wird. Das Netzwerk erhält nicht nur Informationen darüber, was jetzt passiert, sondern auch darüber, was zuvor passiert ist ...

. , . , . , . , . , , . . , .



t . , t = 0 — , t + 1 — . () . , . — .



t, — t + 1.

Ein wiederkehrendes neuronales Netzwerk kann wie in Abb. 1 dargestellt werden. 8.3: Die Kreise entsprechen ganzen Schichten eines vorwärtsgerichteten neuronalen Netzwerks, das aus einem oder mehreren Neuronen besteht. Die Ausgabe der verborgenen Schicht wird wie gewohnt vom Netzwerk ausgegeben, kommt dann aber als eigene Eingabe (verborgene Schicht) zusammen mit den üblichen Eingabedaten des nächsten Zeitschritts zurück. Das Diagramm zeigt diese Rückkopplungsschleife als einen Bogen, der vom Ausgang der Schicht zurück zum Eingang führt.



Eine einfachere (und häufigere) Möglichkeit, diesen Prozess zu veranschaulichen, ist die Netzwerkbereitstellung. Abbildung 8.4 zeigt ein verkehrtes Netzwerk mit zwei Durchläufen der Zeitvariablen (t) - Schichten für die Schritte t + 1 und t + 2.





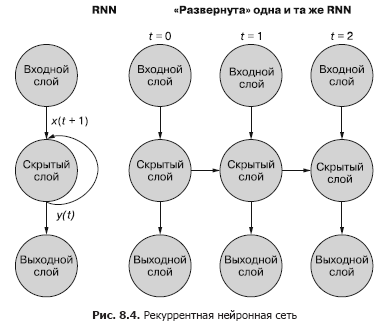
Jeder der Zeitschritte entspricht einer erweiterten Version desselben neuronalen Netzwerks in Form einer Neuronensäule. Es ist, als würde man sich zu einem bestimmten Zeitpunkt ein Skript oder einzelne Videobilder eines neuronalen Netzwerks ansehen. Das Netz rechts repräsentiert eine zukünftige Version des Netzes links. Das Ausgangssignal der verborgenen Schicht zum Zeitpunkt (t) wird zusammen mit den Eingangsdaten für den nächsten Zeitschritt (t + 1) rechts zum Eingang der verborgenen Schicht zurückgeführt. Noch einmal. Das Diagramm zeigt zwei Iterationen dieser Bereitstellung, insgesamt drei Spalten von Neuronen für t = 0, t = 1 und t = 2.



Alle vertikalen Routen in diesem Diagramm sind völlig analog, sie zeigen die gleichen Neuronen. Sie reflektieren das gleiche neuronale Netzwerk zu verschiedenen Zeitpunkten. Diese Visualisierung ist nützlich, um die Vorwärts- und Rückwärtsbewegung von Informationen über das Netzwerk während der Rückübertragung eines Fehlers zu demonstrieren. Denken Sie jedoch daran, wenn Sie sich diese drei bereitgestellten Netzwerke ansehen: Es handelt sich um unterschiedliche Snapshots desselben Netzwerks mit denselben Gewichten.



Schauen wir uns die ursprüngliche Darstellung des wiederkehrenden neuronalen Netzwerks genauer an, bevor wir es bereitstellen, und zeigen wir die Beziehung zwischen den Eingangssignalen und den Gewichten. Die einzelnen Schichten dieses RNN sehen wie in Fig. 1 gezeigt aus. 8.5 und 8.6.





Alle latenten Zustandsneuronen haben einen Satz von Gewichten, die auf jedes der Elemente jedes der Eingangsvektoren angewendet werden, wie in einem herkömmlichen Feedforward-Netzwerk. In diesem Schema erschien jedoch ein zusätzlicher Satz trainierbarer Gewichte, die auf die Ausgangssignale versteckter Neuronen aus dem vorherigen Zeitschritt angewendet werden. Das Netzwerk wählt durch Training die geeigneten Gewichte (Wichtigkeit) früherer Ereignisse aus, wenn die Sequenz Token für Token eingegeben wird.

«», t = 0 t – 1. «» , , . t = 0 . , .

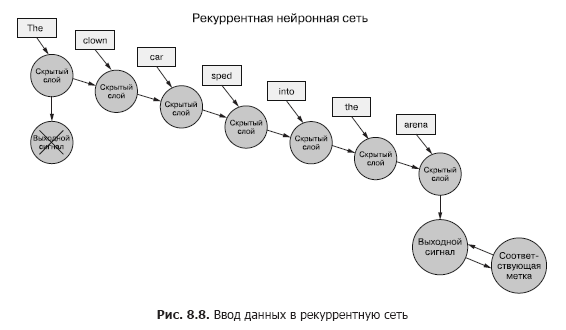
Stellen Sie sich vor, Sie haben eine Reihe von Dokumenten, von denen jedes ein beschriftetes Beispiel ist. Und anstatt wie im vorherigen Kapitel (Abbildung 8.7) den gesamten Satz von Wortvektoren für jedes Sample an das Faltungsnetzwerk zu übergeben, übertragen wir die Sample-Daten Token für Token an das RNN (Abbildung 8.8).





Wir übergeben einen Wortvektor für das erste Token und erhalten die Ausgabe unseres wiederkehrenden neuronalen Netzwerks. Dann übertragen wir den zweiten Token und damit das Ausgangssignal vom ersten! Danach übertragen wir den dritten Token zusammen mit dem Ausgangssignal vom zweiten! Usw. Jetzt gibt es in unserem neuronalen Netzwerk Konzepte von "vor" und "nach", Ursache und Wirkung, einige, wenn auch vage, Zeitvorstellungen (siehe Abb. 8.8).





Jetzt erinnert sich unser Netzwerk schon an etwas! Bis zu einem gewissen Grad. Es sind noch ein paar Dinge zu klären. Erstens, wie kann eine Rückausbreitung eines Fehlers in einer solchen Struktur auftreten?

8.1.1. Rückübertragung eines Zeitfehlers

In allen oben diskutierten Netzwerken gab es eine Zielbezeichnung (Zielvariable), und RNN ist keine Ausnahme. Wir haben jedoch nicht das Konzept einer Beschriftung für jedes Token, und es gibt nur eine Beschriftung für alle Token jedes Beispieltextes. Wir haben nur Etiketten für Beispieldokumente.

Wir sprechen von Token als Eingabe in das Netzwerk bei jedem Zeitschritt, aber wiederkehrende neuronale Netzwerke können auch mit beliebigen Zeitreihendaten arbeiten. Token können beliebig, diskret oder kontinuierlich sein: Wetterstationsablesungen, Notizen, Symbole in einem Satz usw.

Hier vergleichen wir zuerst die Ausgabe des Netzwerks im letzten Zeitschritt mit dem Cue. Dies ist, was wir (vorerst) einen Fehler nennen werden, nämlich unser Netzwerk versucht, ihn zu minimieren. Es gibt jedoch einen kleinen Unterschied zu den vorherigen Kapiteln. Eine gegebene Datenprobe wird in kleinere Teile aufgeteilt, die nacheinander in das neuronale Netzwerk eingespeist werden. Anstatt die Ausgabe für jedes dieser Unterbeispiele direkt zu verwenden, senden wir sie jedoch an das Netzwerk zurück.



Bisher interessiert uns nur das endgültige Ausgangssignal. Jeder der Token in der Sequenz wird in das Netzwerk eingespeist, und die Verluste werden basierend auf der Ausgabe des letzten Zeitschritts (Token) berechnet (Abbildung 8.9).





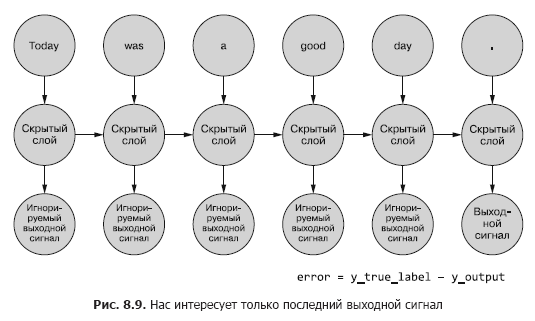
Es muss ermittelt werden, ob und für wie viel Gewicht ein Fehler für ein bestimmtes Beispiel vorliegt. In Kapitel 5 haben wir Ihnen gezeigt, wie Sie einen Fehler über ein normales Netzwerk zurückbreiten können. Und wir wissen, dass das Ausmaß der Gewichtskorrektur von seinem (diesem Gewicht) Beitrag zum Fehler abhängt. Wir können ein Token aus einer Abtastsequenz in den Eingang des Netzwerks einspeisen und den Fehler für den vorherigen Zeitschritt basierend auf seinem Ausgangssignal berechnen. Hier scheint die Idee, einen Fehler in der Zeit zurückzubreiten, alles zu verwirren.



Man kann es sich jedoch einfach als einen zeitgebundenen Prozess vorstellen. Bei jedem Zeitschritt werden Token, beginnend mit dem ersten bei t = 0, einzeln dem Eingang des vorgelagerten versteckten Neurons zugeführt - der nächsten Spalte in Abb. 8.9. In diesem Fall wird das Netzwerk erweitert und zeigt die nächste Spalte des Netzwerks an, die bereits bereit ist, das nächste Token in der Sequenz zu empfangen. Latente Neuronen entfalten sich nacheinander, wie eine Spieluhr oder ein mechanisches Klavier. Wenn alle Elemente der Beispiele in das Netzwerk eingespeist werden, muss am Ende nichts mehr bereitgestellt werden, und wir erhalten die endgültige Bezeichnung für die für uns interessante Zielvariable, mit der der Fehler berechnet und die Gewichte angepasst werden können. Wir sind gerade den ganzen Weg durch das Berechnungsdiagramm für dieses abgerollte Netz gegangen.



Derzeit betrachten wir die Eingabedaten als allgemein statisch. Sie können im gesamten Diagramm verfolgen, welches Eingangssignal zu welchem ​​Neuron geht. Und da wir wissen, wie welches Neuron funktioniert, können wir den Fehler entlang der Kette auf demselben Weg zurückgeben, wie im Fall eines herkömmlichen neuronalen Feedforward-Netzwerks.



Um den Fehler wieder auf die vorherige Ebene zu übertragen, verwenden wir die Kettenregel. Anstelle der vorherigen Schicht wird der Fehler in der Vergangenheit auf dieselbe Schicht übertragen, als ob alle bereitgestellten Netzwerkvarianten unterschiedlich wären (Abbildung 8.10). Dies ändert nichts an der Berechnungsmathematik.





Der Fehler wird vom letzten Schritt zurück übertragen. Der Gradient eines früheren Zeitschritts relativ zu einem neueren wird berechnet. Nach der Berechnung aller einzelnen tokenbasierten Gradienten bis zu Schritt t = 0 für dieses Beispiel werden die Änderungen aggregiert und auf einen Satz von Gewichten angewendet.

8.1.2. Wann was zu aktualisieren

Wir haben unser seltsames RNN in ein normales neuronales Feedforward-Netzwerk verwandelt, daher sollte die Aktualisierung der Gewichte nicht allzu schwierig sein. Es gibt jedoch eine Einschränkung. Der Trick ist, dass die Gewichte in einem anderen Zweig des neuronalen Netzwerks überhaupt nicht aktualisiert werden. Jeder Zweig repräsentiert dasselbe Netzwerk zu unterschiedlichen Zeitpunkten. Die Gewichte für jeden Zeitschritt sind gleich (siehe Abbildung 8.10).



Eine einfache Lösung für dieses Problem besteht darin, Korrekturen für die Gewichte in jedem der Zeitschritte mit einer Verzögerung bei der Aktualisierung zu berechnen. In einem Feedforward-Netzwerk werden alle Aktualisierungen der Gewichte unmittelbar nach der Berechnung aller Gradienten für ein bestimmtes Eingangssignal berechnet. Und hier ist es genau das gleiche, aber Aktualisierungen werden verschoben, bis wir zum anfänglichen (Null-) Zeitschritt für bestimmte Eingabe-Beispieldaten gelangen.



Die Berechnung des Gradienten sollte auf den Werten der Gewichte basieren, bei denen sie diesen Beitrag zum Fehler geleistet haben. Hier ist der überwältigendste Teil: Das Gewicht zum Zeitpunkt t trug in irgendeiner Weise zum Fehler bei. Und das gleiche Gewicht erhält zum Zeitpunkt t + 1 ein weiteres Eingangssignal, was bedeutet, dass es einen anderen Beitrag zum Fehler leistet.



Sie können die verschiedenen Änderungen der Gewichte in jedem Zeitschritt berechnen, zusammenfassen und dann die gruppierten Änderungen als letzten Schritt in der Trainingsphase auf die Gewichte der verborgenen Ebene anwenden.

, . , , . , , . , .

Echte Magie. Im Falle einer Rückwärtsausbreitung des Zeitfehlers kann ein einzelnes Gewicht in einer Richtung zu einem Zeitschritt t (abhängig von seiner Reaktion auf das Eingangssignal zu einem Zeitschritt t) und dann in der anderen Richtung zu einem Zeitschritt t - 1 (gemäß) korrigiert werden wie es im Zeitschritt t - 1) für eine Datenprobe auf das Eingangssignal reagierte! Denken Sie daran, dass neuronale Netze im Allgemeinen auf der Minimierung der Verlustfunktion basieren, unabhängig von der Komplexität der Zwischenschritte. Insgesamt optimiert das Netzwerk diese komplexe Funktion. Da die Gewichtsaktualisierung nur einmal für die Beispieldaten angewendet wird, stoppt das Netzwerk (wenn es überhaupt konvergiert, natürlich) schließlich bei dem in diesem Sinne optimalen Gewicht für ein bestimmtes Eingangssignal und ein bestimmtes Neuron.

Die Ergebnisse der vorherigen Schritte sind weiterhin wichtig

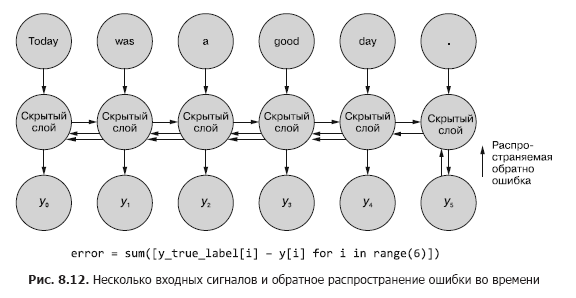
Manchmal ist die gesamte Folge von Werten wichtig, die in allen Zwischenzeitschritten generiert wurden. In Kapitel 9 geben wir Beispiele für Situationen, in denen die Ausgabe eines bestimmten Zeitschritts t genauso wichtig ist wie die Ausgabe des letzten Zeitschritts. In Abb. 8.11 zeigt eine Methode zum Sammeln von Fehlerdaten für jeden Zeitschritt und zum Zurückgeben dieser Daten, um alle Netzwerkgewichte zu korrigieren.





Dieser Prozess ähnelt der üblichen zeitlichen Rückausbreitung eines Fehlers für n Zeitschritte. In diesem Fall verbreiten wir den Fehler gleichzeitig aus mehreren Quellen zurück. Aber wie im ersten Beispiel sind die Gewichtsanpassungen additiv. Der Fehler breitet sich vom letzten Zeitschritt am Anfang zum ersten mit der Summe der Änderungen in jedem der Gewichte aus. Dann passiert dasselbe mit dem Fehler, der im vorletzten Zeitschritt berechnet wurde und alle Änderungen bis zu t = 0 summiert. Dieser Vorgang wird wiederholt, bis wir den Zeitschritt Null mit Rückausbreitung des Fehlers dafür erreichen, als wäre er der einzige. Dann werden die kumulativen Änderungen auf einmal auf die entsprechende verborgene Ebene angewendet.



In Abb. Abbildung 8.12 zeigt, wie sich der Fehler von jedem Ausgangssignal bis zu t = 0 ausbreitet und dann vor der endgültigen Korrektur der Gewichte aggregiert wird. Dies ist die Hauptidee dieses Abschnitts. Wie im Fall eines herkömmlichen vorwärtsgerichteten neuronalen Netzes werden die Gewichte erst aktualisiert, nachdem die vorgeschlagene Änderung der Gewichte für den gesamten Rückausbreitungsschritt für ein gegebenes Eingangssignal (oder einen Satz von Eingangssignalen) berechnet wurde. Im Fall von RNN umfasst die Fehlerausbreitung Aktualisierungen bis zum Zeitpunkt t = 0.



Eine frühere Aktualisierung der Gewichte würde die Gradientenberechnungen mit der Rückwärtsfehlerausbreitung zu früheren Zeitpunkten verzerren. Denken Sie daran, dass Farbverläufe relativ zu einem bestimmten Gewicht berechnet werden. Wenn dieses Gewicht zu früh aktualisiert wird, beispielsweise zum Zeitpunkt t, ändert sich bei der Berechnung des Gradienten zum Zeitpunkt t - 1 der Gewichtswert (denken Sie daran, dass dies die gleiche Position des Gewichts im Netzwerk ist). Und wenn der Gradient basierend auf dem Eingangssignal aus dem Zeitschritt t - 1 berechnet wird, werden die Berechnungen verzerrt. In diesem Fall wird das Gewicht für das, was "nicht schuld" ist, mit einer Geldstrafe (oder Belohnung) belegt!

Über die Autoren

Hobson Lane(Hobson Lane) verfügt über 20 Jahre Erfahrung im Aufbau autonomer Systeme, die wichtige Entscheidungen zum Nutzen der Menschen treffen. Bei Talentpair brachte Hobson Maschinen bei, Lebensläufe weniger voreingenommen zu lesen und zu verstehen als die meisten Personalchefs. Bei Aira half er beim Aufbau ihres ersten Chatbots, der die Welt für Blinde interpretieren soll. Hobson ist ein leidenschaftlicher Bewunderer der Offenheit und Gemeinschaftsorientierung von AI. Er leistet aktive Beiträge zu Open Source-Projekten wie Keras, Scikit-Learn, PyBrain, PUGNLP und ChatterBot. Derzeit ist er an offenen Forschungs- und Bildungsprojekten für Total Good beteiligt, einschließlich der Erstellung eines virtuellen Open-Source-Assistenten. Er hat zahlreiche Artikel veröffentlicht, Vorträge bei AIAA, PyCon,PAIS und IEEE und hat mehrere Patente auf dem Gebiet der Robotik und Automatisierung erhalten.



Hannes Max Hapke ist Elektrotechniker und Ingenieur für maschinelles Lernen. In der High School interessierte er sich für neuronale Netze, als er studierte, wie man neuronale Netze auf Mikrocontrollern berechnet. Später am College wandte er die Prinzipien neuronaler Netze auf das effiziente Management von Kraftwerken für erneuerbare Energien an. Hannes ist begeistert von der Automatisierung von Softwareentwicklung und Pipelines für maschinelles Lernen. Er hat Deep-Learning-Modelle und Pipelines für maschinelles Lernen für die Rekrutierungs-, Energie- und Gesundheitsbranche mitverfasst. Hannes hat auf verschiedenen Konferenzen wie OSCON, Open Source Bridge und Hack University Präsentationen zum maschinellen Lernen gehalten.



Cole Howard(Cole Howard) ist ein Praktiker des maschinellen Lernens, ein NLP-Praktiker und ein Schriftsteller. Als ewiger Mustersucher befand er sich in der Welt der künstlichen neuronalen Netze. Zu seinen Entwicklungen zählen umfangreiche Empfehlungssysteme für den Handel über das Internet und fortschrittliche neuronale Netze für ultrahochdimensionale Maschinenintelligenzsysteme (tiefe neuronale Netze), die bei Kaggle-Wettbewerben an erster Stelle stehen. Er hat auf den Konferenzen Open Source Bridge und Hack University Vorträge über Faltungs-Neuronale Netze, wiederkehrende Neuronale Netze und ihre Rolle bei der Verarbeitung natürlicher Sprache gehalten.





»Weitere Details zum Buch finden Sie auf der Website des Verlags.

» Inhaltsverzeichnis

» Auszug



Für Habitaner 25% Rabatt auf den Gutschein - NLP



Nach Zahlung der Papierversion des Buches wird ein E-Book an die E-Mail gesendet.