
Bei der Entwicklung eines Spiels in völlig unterschiedlichen Genrekategorien kann es erforderlich sein, jedes Spielobjekt entlang einer glatten Kurve mit konstanter oder kontrollierter Geschwindigkeit zu "starten", sei es ein Lastwagen, der sich von Stadt A nach Stadt B bewegt, eine Rakete, die auf einer gerissenen Flugbahn abgefeuert wird, oder ein feindliches Flugzeug ein festgelegtes Manöver durchführen.
Wahrscheinlich kennt oder hört jeder, der mit dem Thema zu tun hat, Bézier-Kurven, B-Splines, Hermite-Splines und andere Interpolations- und Glättungs-Splines und würde in der beschriebenen Situation absolut richtig vorschlagen, eine davon zu verwenden, aber nicht alles ist so einfach wie wir möchten.
In unserem Fall ist ein Spline eine Funktion, die eine Reihe von Eingabeparametern (Kontrollpunkten) und den Wert des Arguments anzeigt (normalerweise mit Werten von 0 bis 1) zu einem Punkt in einer Ebene oder im Raum. Die resultierende Kurve ist der Wertesatz der Spline-Funktion für .
Betrachten Sie als Beispiel die kubischeBezier-Kurve, die durch die folgende Gleichung gegeben ist:


Kubische Bezierkurve
Die Abbildung zeigt zwei kubische Bezierkurven, die durch vier Punkte angegeben sind (die Kurve verläuft durch zwei von ihnen, die verbleibenden zwei definieren die Krümmung).
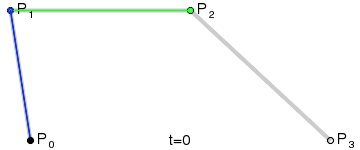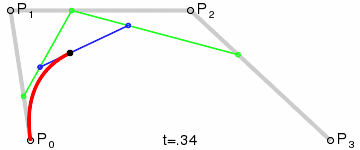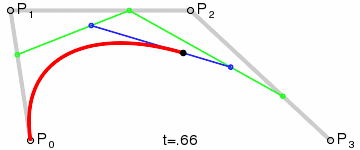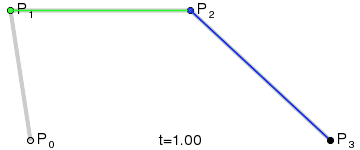
Animation zur Anzeige des Parameters t auf einem Kurvenpunkt
Um aus den Kurvenabschnitten eine komplexere und variablere Route zu erstellen, können diese in einer Kette verbunden werden, wobei ein gemeinsames
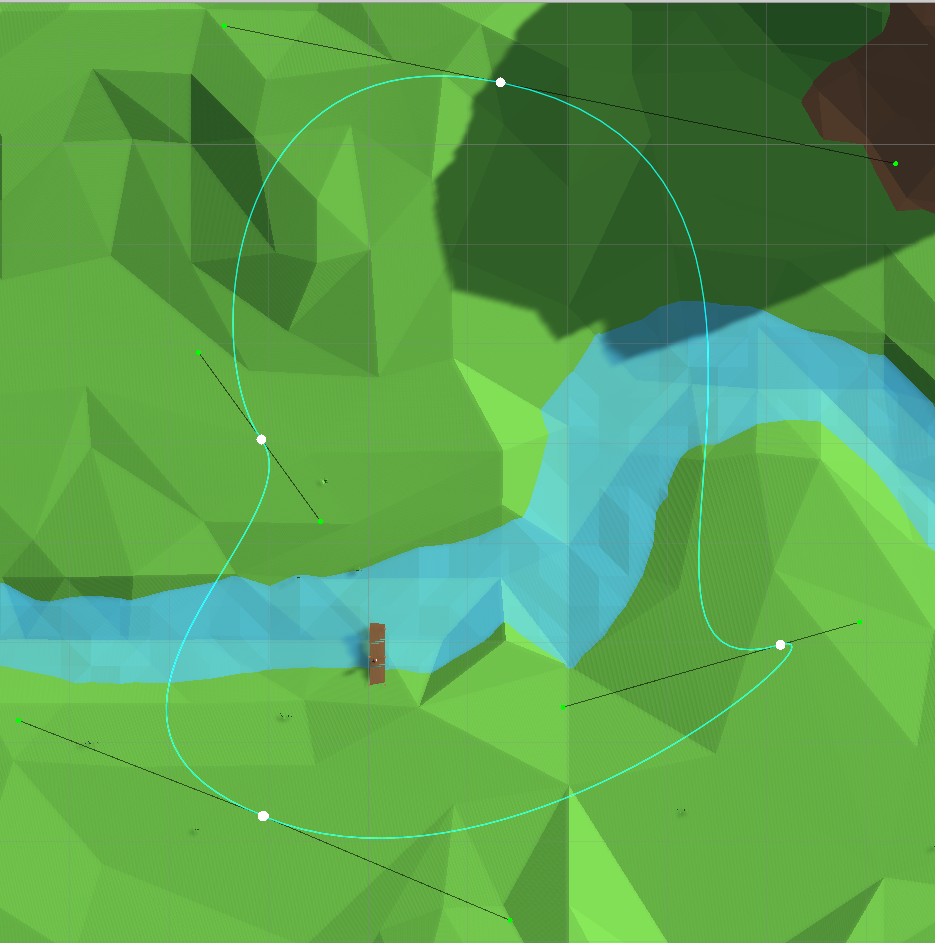
Punktglied verbleibt: Stückweiser Spline Wir haben
die Aufgabe und Parametrisierung der Route herausgefunden und wenden uns nun der Hauptfrage zu. Damit sich unsere bedingte Ebene mit konstanter Geschwindigkeit entlang der Route bewegen kann, müssen wir jederzeit in der Lage sein, einen Punkt auf der Kurve zu berechnen, abhängig von der zurückgelegten Strecke entlang dieser Kurve. , während nur die Position eines Punktes auf der Kurve aus dem Wert des Parameters berechnet werden kann (Funktion ). In diesem Stadium beginnen Schwierigkeiten.
Mein erster Gedanke war eine lineare Abbildung und berechnen aus dem resultierenden Wert - einfach, rechnerisch billig, im Allgemeinen, was Sie brauchen. Das Problem bei dieser Methode ist sofort offensichtlich - tatsächlich die zurückgelegte Strecke

hängt ab von nichtlinear, und um dies sicherzustellen, reicht es aus, entlang der gleichmäßig verteilten Route anzuordnen Punkte: Punkte"gleichmäßig" auf dem Weg verteilt Das Flugzeug verlangsamt sich in einigen Abschnitten und beschleunigt in anderen, was diese Methode der Parametrisierung der Kurve zur Lösung des beschriebenen Problems völlig unanwendbar macht wurde verfolgt):Visualisierung der falschen Parametrisierung der Kurve Nach Rücksprache mit einer Suchmaschine aufStackoverflowundYoutubeentdeckte ich einen zweiten Berechnungsweg


, nämlich die Darstellung der Kurve als stückweise lineare Funktion (Berechnung eines Satzes von Punkten, die entlang der Kurve gleich weit voneinander entfernt sind):
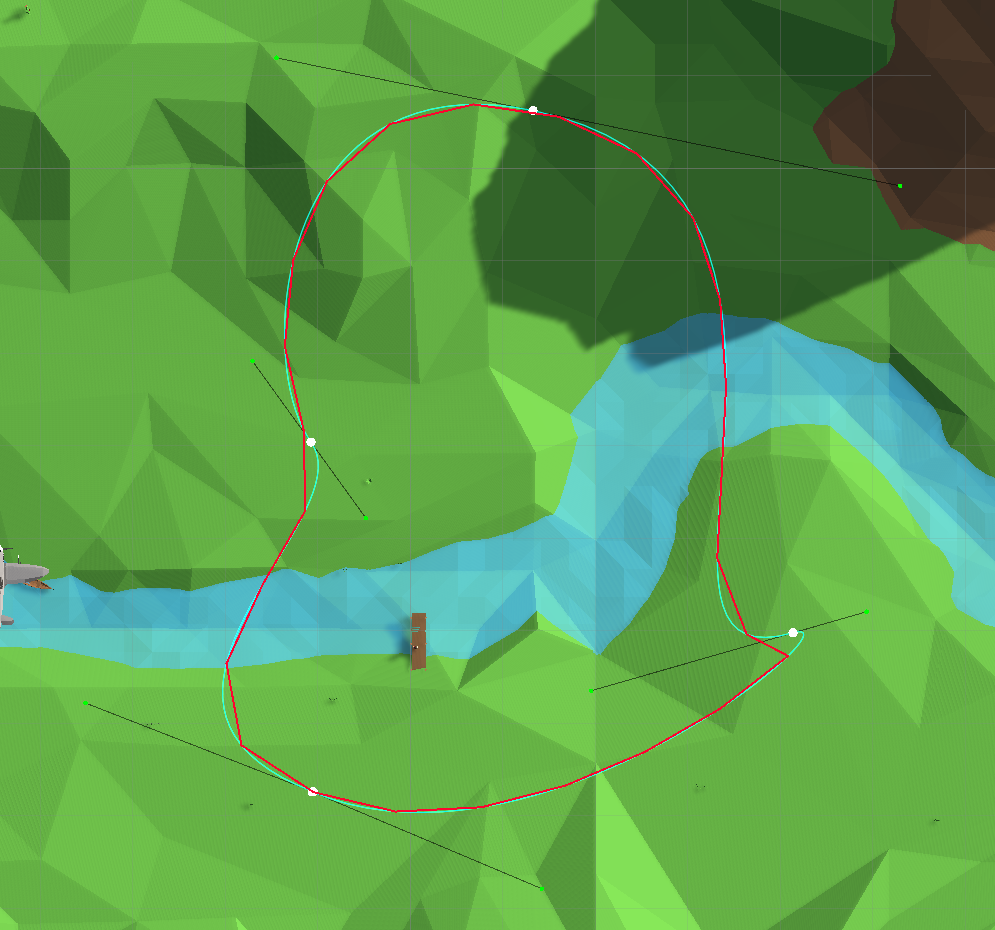
Darstellung der Kurve als stückweise linearer Spline
Dieses Verfahren ist iterativ: Es wird ein kleiner Schritt ausgeführt bewegen wir uns mit ihm entlang einer Kurve und summieren die zurückgelegte Strecke als Länge eines stückweise linearen Splines, bis die angegebene Strecke zurückgelegt ist. Danach wird der Punkt gespeichert und der Vorgang fortgesetzt.
Beispielcode
public Vector2[] CalculateEvenlySpacedPoints(float spacing, float resolution = 1)
{
List<Vector2> evenlySpacedPoints = new List<Vector2>();
evenlySpacedPoints.Add(points[0]);
Vector2 previousPoint = points[0];
float dstSinceLastEvenPoint = 0;
for (int segmentIndex = 0; segmentIndex < NumSegments; segmentIndex++)
{
Vector2[] p = GetPointsInSegment(segmentIndex);
float controlNetLength = Vector2.Distance(p[0], p[1]) + Vector2.Distance(p[1], p[2]) + Vector2.Distance(p[2], p[3]);
float estimatedCurveLength = Vector2.Distance(p[0], p[3]) + controlNetLength / 2f;
int divisions = Mathf.CeilToInt(estimatedCurveLength * resolution * 10);
float t = 0;
while (t <= 1)
{
t += 1f/divisions;
Vector2 pointOnCurve = Bezier.EvaluateCubic(p[0], p[1], p[2], p[3], t);
dstSinceLastEvenPoint += Vector2.Distance(previousPoint, pointOnCurve);
while (dstSinceLastEvenPoint >= spacing)
{
float overshootDst = dstSinceLastEvenPoint - spacing;
Vector2 newEvenlySpacedPoint = pointOnCurve + (previousPoint - pointOnCurve).normalized * overshootDst;
evenlySpacedPoints.Add(newEvenlySpacedPoint);
dstSinceLastEvenPoint = overshootDst;
previousPoint = newEvenlySpacedPoint;
}
previousPoint = pointOnCurve;
}
}
return evenlySpacedPoints.ToArray();
}Und anscheinend ist das Problem gelöst, da Sie die Route in viele Segmente aufteilen und genießen können, wie reibungslos und gemessen sich das Objekt bewegt, da die Berechnung eines Punkts auf einer stückweise linearen Funktion eine einfache und schnelle Angelegenheit ist. Dieser Ansatz hat aber auch ganz offensichtliche Nachteile, die mich verfolgt haben - ein ziemlich kostspieliges Verfahren zum Ändern des Partitionsschritts oder der Kurvengeometrie und die Notwendigkeit, ein Gleichgewicht zwischen Genauigkeit (mehr Speicherverbrauch) und Speichereinsparungen zu finden (die "unterbrochene" Route wird deutlicher).
Infolgedessen suchte ich weiter und stieß auf einen ausgezeichneten Artikel "Bewegen entlang einer Kurve mit spezifizierter Geschwindigkeit" , auf dessen Grundlage weitere Überlegungen basieren.
Der Geschwindigkeitswert kann berechnet werden alswo ist eine Spline-Funktion. Um das Problem zu lösen, müssen Sie die Funktion finden , wobei ist die Länge des Bogens vom Startpunkt zum gewünschten, und dieser Ausdruck legt die Beziehung zwischen fest und .
Mit der Substitution von Differenzierungsvariablen können wir schreiben
Unter Berücksichtigung, dass die Geschwindigkeit eine nicht negative Größe ist, erhalten wir
als durch die Bedingung, dass der Modul des Geschwindigkeitsvektors unverändert bleibt (im Allgemeinen,ist nicht gleich eins, sondern eine Konstante, aber zur Vereinfachung der Berechnungen nehmen wir diese Konstante gleich eins).
Jetzt bekommen wir das Verhältnis zwischen und explizit:
woher die Gesamtlänge der Kurve wird offensichtlich berechnet als . Mit der resultierenden Formel ist es möglich, den Wert des Arguments zu haben , berechnen Sie die Länge des Bogens bis zu dem Punkt, an dem dieser Wert liegt angezeigt.
Wir sind an der umgekehrten Operation interessiert, dh der Berechnung des Wertes des Arguments entlang einer gegebenen Bogenlänge :
Da es keinen allgemeinen analytischen Weg gibt, um die Umkehrfunktion zu finden, müssen Sie nach einer numerischen Lösung suchen. Wir bezeichnenFür ein gegebenes , Sie müssen einen solchen Wert finden bei denen . So wurde die Aufgabe zur Aufgabe, die Wurzel der Gleichung zu finden, mit der Newtons Methode perfekt umgehen kann.
Das Verfahren bildet eine Folge von Approximationen des Formulars
Wo
Berechnen Zur Berechnung ist F ( t ) erforderlich , dessen Berechnung wiederum eine numerische Integration erfordert.
Wahl als anfängliche Annäherung sieht jetzt vernünftig aus (erinnern Sie sich an den ersten Ansatz zur Lösung des Problems).
Als nächstes iterieren wir mit der Newtonschen Methode, bis der Lösungsfehler akzeptabel wird oder die Anzahl der durchgeführten Iterationen unerschwinglich groß ist.
Es gibt ein potenzielles Problem bei der Verwendung der Newton-Standardmethode. Funktion nimmt seit seiner Ableitung nicht abist nicht negativ. Ist die zweite Ableitung kann sich als negativ herausstellen, wodurch die Newtonsche Methode außerhalb des Definitionsbereichs konvergieren kann ... Der Autor des Artikels schlägt vor, eine Modifikation der Newtonschen Methode zu verwenden, die, wenn das nächste Iterationsergebnis nach der Newtonschen Methode nicht in das aktuelle Intervall fällt, das die Wurzel begrenzt, stattdessen die Mitte des Intervalls auswählt ( Dichotomiemethode ). Unabhängig vom Ergebnis der Berechnung bei der aktuellen Iteration wird der Bereich eingeengt, was bedeutet, dass die Methode zur Wurzel konvergiert.
Es bleibt die Wahl der Methode der numerischen Integration - ich habe die Quadraturen der Gauß-Methode verwendet , da sie bei geringen Kosten ein ziemlich genaues Ergebnis liefert.
Funktionscode zur Berechnung von t (s)
public float ArcLength(float t) => Integrate(x => TangentMagnitude(x), 0, t);
private float Parameter(float length)
{
float t = 0 + length / ArcLength(1);
float lowerBound = 0f;
float upperBound = 1f;
for (int i = 0; i < 100; ++i)
{
float f = ArcLength(t) - length;
if (Mathf.Abs(f) < 0.01f)
break;
float derivative = TangentMagnitude(t);
float candidateT = t - f / derivative;
if (f > 0)
{
upperBound = t;
if (candidateT <= 0)
t = (upperBound + lowerBound) / 2;
else
t = candidateT;
}
else
{
lowerBound = t;
if (candidateT >= 1)
t = (upperBound + lowerBound) / 2;
else
t = candidateT;
}
}
return t;
}
Funktionscode für numerische Integration
private static readonly (float, float)[] CubicQuadrature =
{(-0.7745966F, 0.5555556F), (0, 0.8888889F), (0.7745966F, 0.5555556F)};
public static float Integrate(Func<float, float> f, in float lowerBound, in float uppedBound)
{
var sum = 0f;
foreach (var (arg, weight) in CubicQuadrature)
{
var t = Mathf.Lerp(lowerBound, uppedBound, Mathf.InverseLerp(-1, 1, arg));
sum += weight * f(t);
}
return sum * (upperBound - lowerBound) / 2;
}Als nächstes können Sie den Fehler der Newtonschen Methode anpassen und eine genauere Methode zur numerischen Integration auswählen, aber das Problem ist tatsächlich gelöst - ein Algorithmus zur Berechnung des Arguments wurde erstellt Spline für eine bestimmte Bogenlänge. Mehrere Kurvenabschnitte zu einem kombinieren und ein verallgemeinertes Berechnungsverfahren schreibenSie können die Längen aller Segmente speichern und den Index des Segments, in dem Sie eine iterative Prozedur ausführen möchten, mit der modifizierten Newton-Methode vorberechnen.
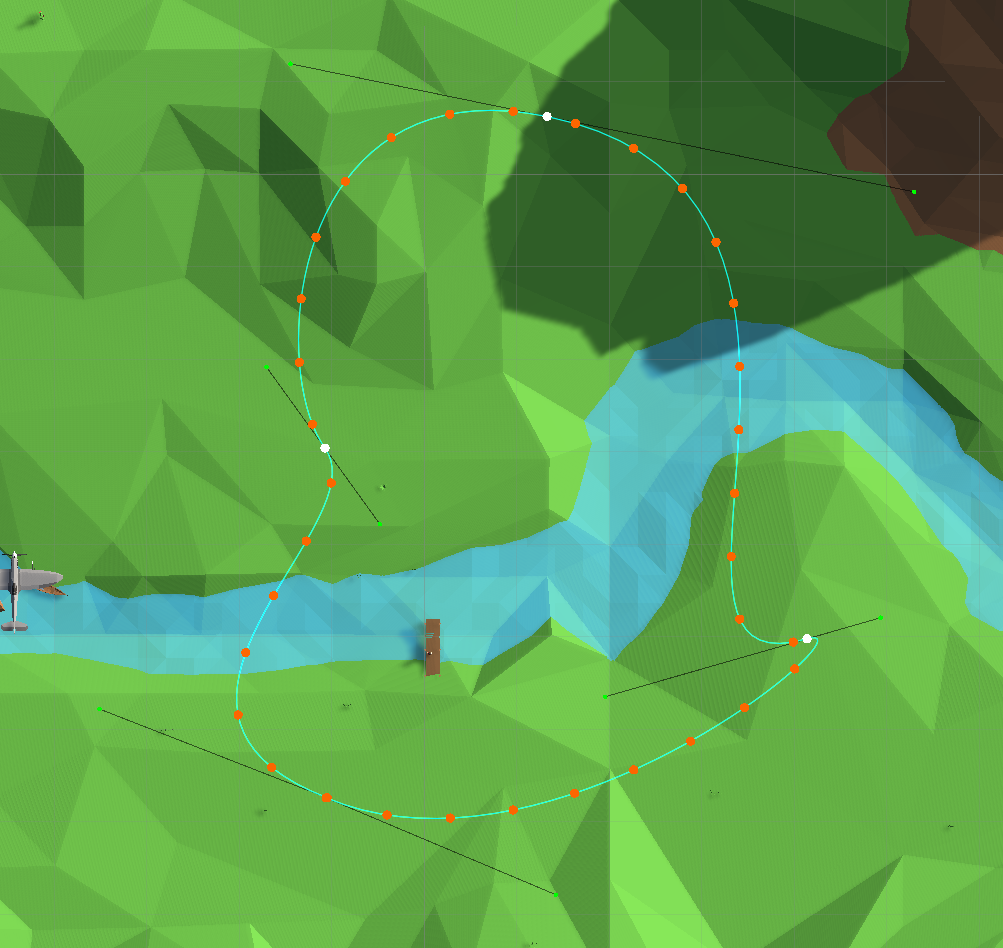
Punkte gleichmäßig auf dem Pfad verteilt

Jetzt bewegt sich die Ebene gleichmäßig.
Daher haben wir verschiedene Möglichkeiten in Betracht gezogen, den Spline relativ zur zurückgelegten Entfernung zu parametrisieren. In dem Artikel, den ich als Quelle verwendet habe, schlägt der Autor vor, die Differentialgleichung als Option numerisch zu lösen, bevorzugt jedoch nach seiner eigenen Bemerkung die modifizierte Methode Newton:
Ich bevorzuge den Newton-Methode-Ansatz, da t im Allgemeinen schneller berechnet werden kann als mit Differentialgleichungslösern.
Abschließend werde ich eine Zeittabelle für die Berechnung der Position eines Punkts auf der Kurve geben, die in den Screenshots in einem Thread auf einem i5-9600K-Prozessor gezeigt wird:
| Anzahl der Berechnungen | Durchschnittliche Zeit, ms |
|---|---|
| 100 | 0,62 |
| 1000 | 6.24 |
| 10000 | 69.01 |
| 100.000 | 672,81 |