
Hallo allerseits, heute werden wir uns mit dem JPEG-Komprimierungsalgorithmus befassen. Viele Menschen wissen nicht, dass JPEG weniger ein Format als ein Algorithmus ist. Die meisten angezeigten JPEG-Bilder befinden sich im JFIF-Format (JPEG File Interchange Format), in dem der JPEG-Komprimierungsalgorithmus angewendet wird. Am Ende des Artikels haben Sie ein viel besseres Verständnis dafür, wie dieser Algorithmus Daten komprimiert und wie Sie Entpackungscode in Python schreiben. Wir werden nicht alle Nuancen des JPEG-Formats berücksichtigen (z. B. progressives Scannen), sondern nur über die grundlegenden Funktionen des Formats sprechen, während wir unseren eigenen Decoder schreiben.
Einführung
Warum einen weiteren Artikel über JPEG schreiben, wenn bereits Hunderte von Artikeln darüber geschrieben wurden? Normalerweise sprechen die Autoren in solchen Artikeln nur über das Format. Sie schreiben keinen Entpack- und Dekodierungscode. Und selbst wenn Sie etwas schreiben, wird es in C / C ++ sein und dieser Code wird für eine breite Palette von Menschen unzugänglich sein. Ich möchte diese Tradition brechen und Ihnen mit Python 3 zeigen, wie ein grundlegender JPEG-Decoder funktioniert. Es wird auf diesem vom MIT entwickelten Code basieren, aber ich werde ihn aus Gründen der Lesbarkeit und Klarheit stark ändern. Den geänderten Code für diesen Artikel finden Sie in meinem Repository .
Verschiedene Teile von JPEG
Beginnen wir mit einem Bild von Ange Albertini . Es listet alle Teile einer einfachen JPEG-Datei auf. Wir werden jedes Segment analysieren und beim Lesen des Artikels werden Sie mehrmals zu dieser Abbildung zurückkehren.
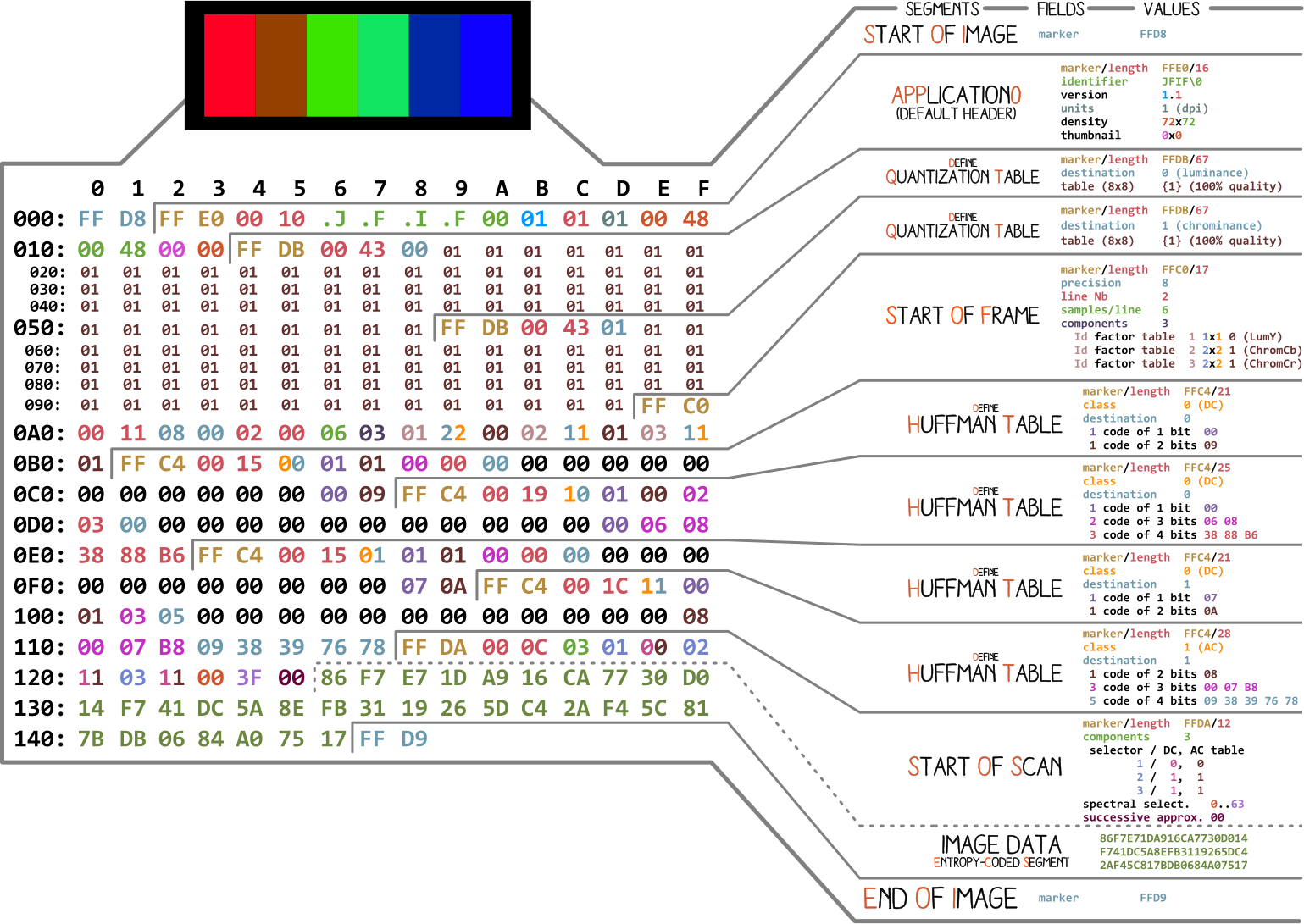
Fast jede Binärdatei enthält mehrere Marker (oder Header). Sie können sich diese als Lesezeichen vorstellen. Sie sind für die Arbeit mit der Datei unerlässlich und werden von Programmen wie file (unter Mac und Linux) verwendet, damit wir die Details der Datei herausfinden können. Markierungen geben genau an, wo bestimmte Informationen in der Datei gespeichert sind. Am häufigsten werden Markierungen entsprechend dem Längenwert (
length) eines bestimmten Segments platziert.
Anfang und Ende der Datei
Der allererste für uns wichtige Marker ist
FF D8. Es definiert den Anfang des Bildes. Wenn wir es nicht finden, können wir davon ausgehen, dass sich der Marker in einer anderen Datei befindet. Der Marker ist nicht weniger wichtig FF D9. Es heißt, dass wir das Ende der Bilddatei erreicht haben. Nach jedem Marker, mit Ausnahme des Bereichs FFD0- FFD9und FF01, kommt sofort der Wert der Segmentlänge dieses Markers. Und die Markierungen am Anfang und Ende der Datei sind immer zwei Bytes lang.
Wir werden mit diesem Bild arbeiten:

Schreiben wir einen Code, um die Start- und Endmarkierungen zu finden.
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
Um die Bytes des Bildes zu entpacken, haben wir struct verwendet .
>HWeist structes an, den Datentyp zu lesen unsigned shortund damit in der Reihenfolge von hoch nach niedrig (Big-Endian) zu arbeiten. JPEG-Daten werden im höchsten bis niedrigsten Format gespeichert. Nur EXIF-Daten können im Little-Endian-Format vorliegen (obwohl dies normalerweise nicht der Fall ist). Und die Größe shortist 2, also übertragen wir unpackzwei Bytes von img_data. Woher wussten wir, was es ist short? Wir wissen, dass die Markierungen in JPEG durch vier hexadezimale Zeichen gekennzeichnet sind : ffd8. Ein solches Zeichen entspricht vier Bits (ein halbes Byte), also entsprechen vier Zeichen genau wie zwei Bytes short.
Nach dem Abschnitt "Scanstart" folgen unmittelbar die gescannten Bilddaten, die keine bestimmte Länge haben. Sie werden bis zum Ende der Dateimarkierung fortgesetzt. Während wir also manuell danach suchen, finden wir die Markierung für den Start des Scans.
Lassen Sie uns nun den Rest der Bilddaten behandeln. Dazu studieren wir zuerst die Theorie und fahren dann mit der Programmierung fort.
JPEG-Codierung
Lassen Sie uns zunächst über die grundlegenden Konzepte und Codierungstechniken sprechen, die in JPEG verwendet werden. Die Codierung erfolgt in umgekehrter Reihenfolge. Nach meiner Erfahrung wird es schwierig sein, die Dekodierung ohne sie herauszufinden.
Die folgende Abbildung ist Ihnen noch nicht klar, aber ich werde Ihnen Hinweise geben, wenn Sie den Kodierungs- und Dekodierungsprozess lernen. Hier sind die Schritte für die JPEG-Codierung ( Quelle ):
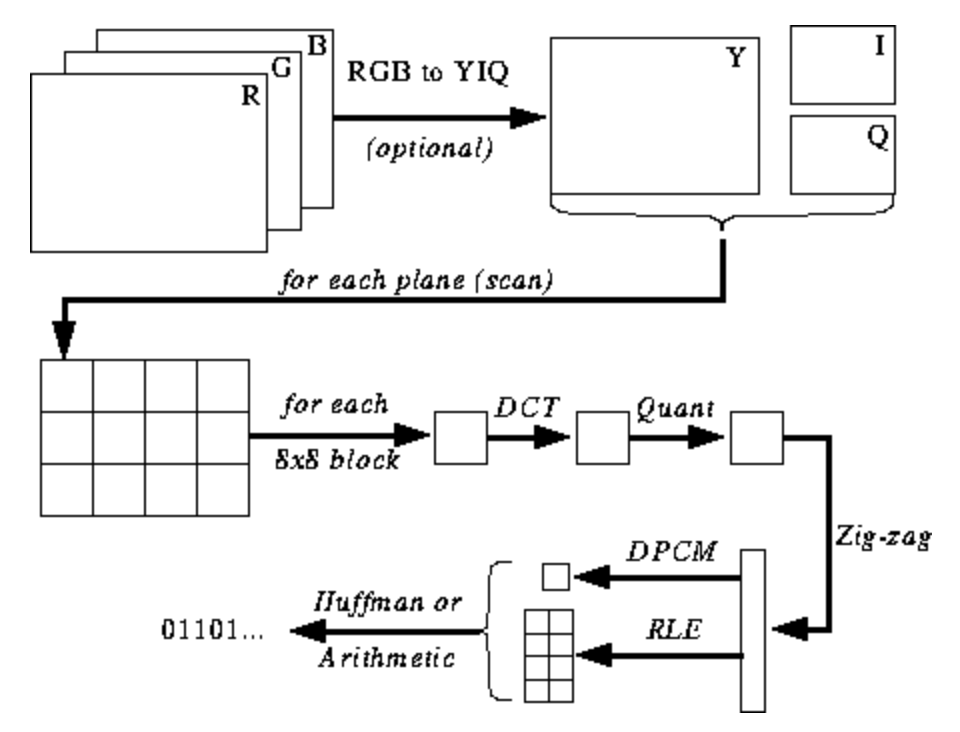
JPEG-Farbraum
Gemäß der JPEG-Spezifikation ( ISO / IEC 10918-6: 2013 (E) Abschnitt 6.1):
- Mit nur einer Komponente codierte Bilder werden als Graustufendaten behandelt, wobei 0 schwarz und 255 weiß ist.
- Mit drei Komponenten codierte Bilder gelten als im YCbCr-Raum codierte RGB-Daten. Wenn das Bild das in Abschnitt 6.5.3 beschriebene APP14-Markersegment enthält, wird die Farbcodierung gemäß den Informationen im APP14-Markersegment als RGB oder YCbCr betrachtet. Die Beziehung zwischen RGB und YCbCr wird gemäß ITU-T T.871 | definiert ISO / IEC 10918-5.
- , , CMYK-, (0,0,0,0) . APP14, 6.5.3, CMYK YCCK APP14. CMYK YCCK 7.
Die meisten Implementierungen des JPEG-Algorithmus verwenden Luminanz und Chrominanz (YUV-Codierung) anstelle von RGB. Dies ist sehr nützlich, da das menschliche Auge hochfrequente Helligkeitsänderungen in kleinen Bereichen nur sehr schlecht erkennen kann, sodass Sie die Frequenz verringern können und die Person den Unterschied nicht bemerkt. Was tut es? Hochkomprimiertes Bild mit nahezu unmerklicher Qualitätsminderung.
Wie bei RGB wird jedes Pixel mit drei Farbbytes (rot, grün und blau) codiert, so dass bei YUV drei Bytes verwendet werden, deren Bedeutung jedoch unterschiedlich ist. Die Y-Komponente definiert die Helligkeit der Farbe (Luminanz oder Luma). U und V definieren die Farbe (Chroma): U ist für den blauen Teil und V für den roten Teil verantwortlich.
Dieses Format wurde zu einer Zeit entwickelt, als das Fernsehen noch nicht so verbreitet war, und die Ingenieure wollten dasselbe Farbcodierungsformat sowohl für Farb- als auch für Schwarzweißfernsehübertragungen verwenden. Lesen Sie mehr dazu hier .
Diskrete Cosinustransformation und Quantisierung
JPEG konvertiert das Bild in 8x8 Pixelblöcke (MCUs, Minimum Coding Unit), ändert den Bereich der Pixelwerte so, dass die Mitte 0 ist, wendet dann eine diskrete Cosinustransformation auf jeden Block an und komprimiert das Ergebnis mithilfe der Quantisierung. Mal sehen, was das alles bedeutet.
Die diskrete Cosinustransformation (DCT) ist eine Methode zur Transformation diskreter Daten in Kombinationen von Cosinuswellen. Das Konvertieren eines Bildes in eine Reihe von Kosinusse sieht auf den ersten Blick wie eine sinnlose Übung aus, aber Sie werden den Grund verstehen, wenn Sie die nächsten Schritte kennenlernen. DCT nimmt einen 8x8-Pixelblock und erklärt, wie dieser Block unter Verwendung einer Matrix von 8x8-Kosinusfunktionen reproduziert werden kann. Weitere Details hier .
Die Matrix sieht folgendermaßen aus:

Wir wenden DCT separat auf jede Pixelkomponente an. Als Ergebnis erhalten wir eine 8x8-Koeffizientenmatrix, die den Beitrag jeder (von allen 64) Kosinusfunktionen in der 8x8-Eingangsmatrix zeigt. In der Matrix der DCT-Koeffizienten befinden sich die größten Werte normalerweise in der oberen linken Ecke und die kleinsten in der unteren rechten Ecke. Oben links ist die Kosinusfunktion mit der niedrigsten Frequenz und unten rechts ist die höchste.
Dies bedeutet, dass in den meisten Bildern eine große Menge an Niederfrequenzinformationen und eine kleine Menge an Hochfrequenzinformationen vorhanden sind. Wenn den unteren rechten Komponenten jeder DCT-Matrix der Wert 0 zugewiesen wird, sieht das resultierende Bild für uns gleich aus, da eine Person Hochfrequenzänderungen nicht schlecht unterscheidet. Dies werden wir im nächsten Schritt tun.
Ich habe ein großartiges Video zu diesem Thema gefunden. Schauen Sie, wenn Sie die Bedeutung von PrEP nicht verstehen:
Wir alle wissen, dass JPEG ein verlustbehafteter Komprimierungsalgorithmus ist. Bisher haben wir aber nichts verloren. Wir haben nur Blöcke mit 8x8 YUV-Komponenten, die ohne Informationsverlust in Blöcke mit 8x8 Cosinusfunktionen konvertiert wurden. Die Datenverluststufe ist die Quantisierung.
Quantisierung ist der Prozess, bei dem wir zwei Werte aus einem bestimmten Bereich in einen diskreten Wert umwandeln. In unserem Fall ist dies nur ein schlauer Name, um die höchsten Frequenzkoeffizienten in der resultierenden DCT-Matrix auf 0 zu reduzieren. Wenn Sie ein Bild mit JPEG speichern, werden Sie von den meisten Grafikeditoren gefragt, welche Komprimierungsstufe Sie einstellen möchten. Hier tritt der Verlust von Hochfrequenzinformationen auf. Sie können das Originalbild aus dem resultierenden JPEG-Bild nicht mehr neu erstellen.
Abhängig vom Komprimierungsverhältnis werden unterschiedliche Quantisierungsmatrizen verwendet (lustige Tatsache: Die meisten Entwickler haben Patente zum Erstellen einer Quantisierungstabelle). Wir teilen die DCT-Koeffizientenmatrix Element für Element durch die Quantisierungsmatrix, runden die Ergebnisse auf ganze Zahlen und erhalten die quantisierte Matrix.
Schauen wir uns ein Beispiel an. Angenommen, es gibt eine solche DCT-Matrix:

Und hier ist die übliche Quantisierungsmatrix:
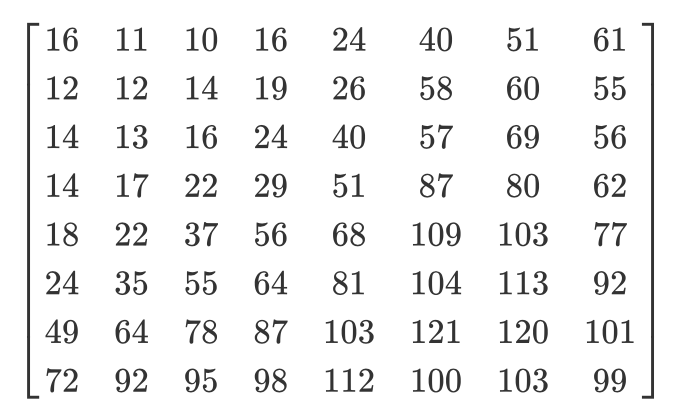
Die quantisierte Matrix sieht folgendermaßen aus:

Obwohl Menschen keine hochfrequenten Informationen sehen können, sieht das Bild zu rau aus, wenn Sie zu viele Daten aus den 8x8-Pixelblöcken entfernen. In einer solchen quantisierten Matrix wird der allererste Wert als DC-Wert bezeichnet, und alle anderen werden als AC-Werte bezeichnet. Wenn wir die DC-Werte aller quantisierten Matrizen nehmen und ein neues Bild erzeugen würden, würden wir eine Vorschau mit einer Auflösung erhalten, die achtmal kleiner als das Originalbild ist.
Ich möchte auch darauf hinweisen, dass wir, da wir die Quantisierung verwendet haben, sicherstellen müssen, dass die Farben in den Bereich von [0,255] fallen. Wenn sie herausfliegen, müssen Sie sie manuell in diesen Bereich bringen.
Zickzack
Nach der Quantisierung verwendet der JPEG-Algorithmus einen Zick-Zack-Scan, um die Matrix in eine eindimensionale Form umzuwandeln:
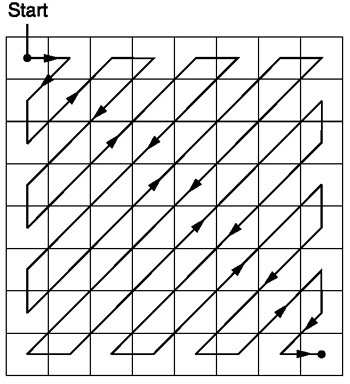
Quelle .
Lassen Sie uns eine solche quantisierte Matrix haben:
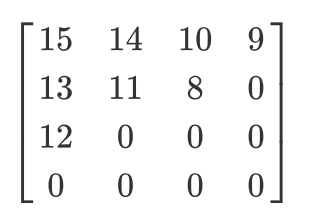
Das Ergebnis des Zick-Zack-Scans lautet dann wie folgt:
[15 14 13 12 11 10 9 8 0 ... 0]
Diese Codierung wird bevorzugt, da sich nach der Quantisierung der größte Teil der niederfrequenten (wichtigsten) Informationen am Anfang der Matrix befindet und der Zick-Zack-Scan diese Daten am Anfang der eindimensionalen Matrix speichert. Dies ist nützlich für den nächsten Schritt, die Komprimierung.
Lauflängencodierung und Delta-Codierung
Die Lauflängencodierung wird verwendet, um sich wiederholende Daten zu komprimieren. Nach dem Zick-Zack-Scan sehen wir, dass am Ende des Arrays meistens Nullen stehen. Die Längencodierung ermöglicht es uns, diesen verschwendeten Speicherplatz zu nutzen und weniger Bytes zu verwenden, um alle diese Nullen darzustellen. Angenommen, wir haben die folgenden Daten:
10 10 10 10 10 10 10
Nach dem Codieren der Serienlängen erhalten wir Folgendes:
7 10
Wir haben 7 Bytes in 2 Bytes komprimiert.
Die Delta-Codierung wird verwendet, um ein Byte relativ zu dem Byte davor darzustellen. Es wird einfacher sein, mit einem Beispiel zu erklären. Geben Sie uns folgende Daten:
10 11 12 13 10 9
Mithilfe der Delta-Codierung können sie wie folgt dargestellt werden:
10 1 2 3 0 -1
In JPEG ist jeder DC-Wert der DCT-Matrix relativ zum vorherigen DC-Wert delta-codiert. Dies bedeutet, dass Sie durch Ändern des allerersten DCT-Koeffizienten des Bildes das gesamte Bild zerstören. Wenn Sie jedoch den ersten Wert der letzten DCT-Matrix ändern, wirkt sich dies nur auf ein sehr kleines Fragment des Bildes aus.
Dieser Ansatz ist nützlich, da der erste DC-Wert des Bildes normalerweise am stärksten variiert und wir die Delta-Codierung verwenden, um die verbleibenden DC-Werte näher an 0 zu bringen, was die Komprimierung mit der Huffman-Codierung verbessert.
Huffman-Codierung
Es ist eine verlustfreie Komprimierungsmethode. Huffman fragte sich einmal: "Was ist die kleinste Anzahl von Bits, mit denen ich freien Text speichern kann?" Als Ergebnis wurde ein Codierungsformat erstellt. Nehmen wir an, wir haben Text:
a b c d e
Normalerweise nimmt jedes Zeichen ein Byte Speicherplatz ein:
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
Dies ist das Prinzip der binären ASCII-Codierung. Was ist, wenn wir das Mapping ändern?
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
Wir brauchen jetzt viel weniger Bits, um denselben Text zu speichern:
a: 000
b: 001
c: 010
d: 100
e: 011
Das ist alles schön und gut, aber was ist, wenn wir noch mehr Platz sparen müssen? Zum Beispiel so:
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
Die Huffman-Codierung ermöglicht eine solche Anpassung mit variabler Länge. Die Eingabedaten werden übernommen, die häufigsten Zeichen werden mit einer kleineren Kombination von Bits und weniger häufigen Zeichen abgeglichen - mit größeren Kombinationen. Und dann werden die resultierenden Zuordnungen in einem Binärbaum gesammelt. In JPEG speichern wir DCT-Informationen mithilfe der Huffman-Codierung. Denken Sie daran, ich habe erwähnt, dass die Delta-Codierung von DC-Werten die Huffman-Codierung erleichtert. Ich hoffe du verstehst jetzt warum. Nach der Delta-Codierung müssen weniger „Zeichen“ gefunden werden, und die Baumgröße wird reduziert.
Tom Scott hat ein großartiges Video, in dem erklärt wird, wie der Huffman-Algorithmus funktioniert. Schauen Sie sich das an, bevor Sie weiterlesen.
Ein JPEG enthält bis zu vier Huffman-Tabellen, die in der "Huffman-Tabelle definieren" gespeichert sind (beginnt mit
0xffc4). DCT-Koeffizienten werden in zwei verschiedenen Huffman-Tabellen gespeichert: in einem DC-Wert aus Zick-Zack-Tabellen, in dem anderen - AC-Werte aus Zick-Zack-Tabellen. Dies bedeutet, dass wir beim Codieren die DC- und AC-Werte der beiden Matrizen kombinieren müssen. DCT-Informationen für Luma- und Chromatizitätskanäle werden separat gespeichert, sodass wir zwei Sätze von DC- und zwei Sätze von AC-Informationen haben, insgesamt 4 Huffman-Tabellen.
Wenn das Bild in Graustufen vorliegt, haben wir nur zwei Huffman-Tabellen (eine für DC und eine für AC), da wir keine Farbe benötigen. Wie Sie vielleicht herausgefunden haben, können zwei verschiedene Bilder sehr unterschiedliche Huffman-Tabellen haben. Daher ist es wichtig, sie in jedem JPEG zu speichern.
Wir kennen jetzt den Hauptinhalt von JPEG-Bildern. Fahren wir mit der Dekodierung fort.
JPEG-Dekodierung
Die Dekodierung kann in Stufen unterteilt werden:
- Extraktion von Huffman-Tabellen und Decodierung von Bits.
- Extrahieren von DCT-Koeffizienten mithilfe von Rollback für Lauflänge und Delta-Codierung.
- Verwenden von DCT-Koeffizienten zum Kombinieren von Kosinuswellen und Rekonstruieren von Pixelwerten für jeden 8x8-Block.
- Konvertieren Sie YCbCr für jedes Pixel in RGB.
- Zeigt das resultierende RGB-Bild an.
Der JPEG-Standard unterstützt vier Komprimierungsformate:
- Base
- Erweiterte Seriennummer
- Progressiv
- Kein Verlust
Wir werden mit grundlegender Komprimierung arbeiten. Es enthält eine Reihe von 8x8 Blöcken, die aufeinander folgen. In anderen Formaten unterscheidet sich die Datenvorlage geringfügig. Um es klar zu machen, habe ich verschiedene Segmente des hexadezimalen Inhalts unseres Bildes eingefärbt:
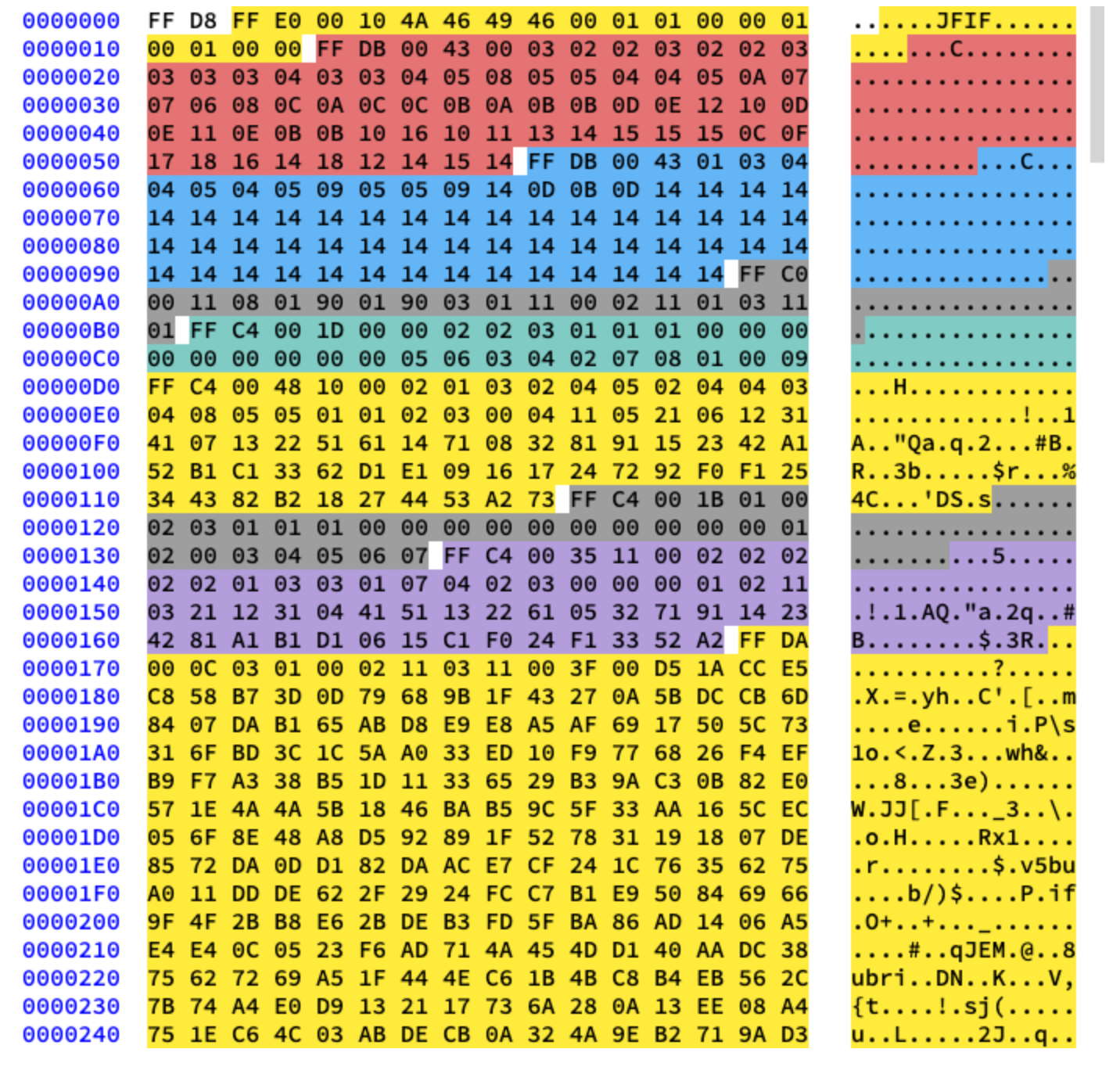
Extrahieren von Huffman-Tabellen
Wir wissen bereits, dass JPEG vier Huffman-Tabellen enthält. Dies ist die letzte Codierung, daher beginnen wir mit der Decodierung. Jeder Abschnitt mit der Tabelle enthält Informationen:
| Feld | Die Größe | Beschreibung |
|---|---|---|
| Marker ID | 2 Bytes | 0xff und 0xc4 identifizieren DHT |
| Länge | 2 Bytes | Tischlänge |
| Informationen zur Huffman-Tabelle | 1 Byte | Bits 0 ... 3: Anzahl der Tabellen (0 ... 3, sonst Fehler) Bit 4: Tabellentyp, 0 = DC-Tabelle, 1 = AC-Tabellen Bits 5 ... 7: nicht verwendet, muss 0 sein |
| Zeichen | 16 Bytes | Die Anzahl der Zeichen mit Codes der Länge 1 ... 16, Summe (n) dieser Bytes ist die Gesamtzahl der Codes, die <= 256 sein müssen |
| Symbole | n Bytes | Die Tabelle enthält Zeichen in der Reihenfolge zunehmender Codelänge (n = Gesamtzahl der Codes). |
Nehmen wir an, wir haben eine Huffman-Tabelle wie diese ( Quelle ):
| Symbol | Huffman-Code | Codelänge |
|---|---|---|
| ein | 00 | 2 |
| b | 010 | 3 |
| c | 011 | 3 |
| d | 100 | 3 |
| e | 101 | 3 |
| f | 110 | 3 |
| G | 1110 | 4 |
| h | 11110 | fünf |
| ich | 111110 | 6 |
| j | 1111110 | 7 |
| k | 11111110 | 8 |
| l | 111111110 | neun |
Es wird in einer JFIF-Datei wie dieser gespeichert (im Binärformat. Ich verwende ASCII nur aus Gründen der Übersichtlichkeit):
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
0 bedeutet, dass wir keinen Huffman-Code der Länge 1 haben. Eine 1 bedeutet, dass wir einen Huffman-Code der Länge 2 haben und so weiter. Im DHT-Abschnitt sind die Daten unmittelbar nach der Klasse und der ID immer 16 Byte lang. Schreiben wir den Code, um Längen und Elemente aus DHT zu extrahieren.
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Nach dem Ausführen des Codes erhalten wir Folgendes:
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
Ausgezeichnet! Wir haben Längen und Elemente. Jetzt müssen Sie Ihre eigene Huffman-Tabellenklasse erstellen, um einen Binärbaum aus den erhaltenen Längen und Elementen zu rekonstruieren. Ich kopiere einfach den Code von hier :
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBitsNimmt die Längen und Elemente, iteriert über die Elemente und fügt sie in eine Liste ein root. Es ist ein Binärbaum und enthält verschachtelte Listen. Sie können im Internet lesen, wie der Huffman-Baum funktioniert und wie eine solche Datenstruktur in Python erstellt wird. Für unser erstes DHT (aus dem Bild am Anfang des Artikels) haben wir folgende Daten, Längen und Elemente:
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00
Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
Nach dem Anruf enthält die
GetHuffmanBitsListe rootdie folgenden Daten:
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTableenthält auch eine Methode GetCode, die durch den Baum geht und eine Huffman-Tabelle verwendet, um die decodierten Bits zurückzugeben. Die Methode empfängt einen Bitstrom als Eingabe - nur eine binäre Darstellung der Daten. Zum Beispiel wird der Bitstrom für abcsein 011000010110001001100011. Zuerst konvertieren wir jedes Zeichen in seinen ASCII-Code, den wir in Binär konvertieren. Erstellen wir eine Klasse, mit deren Hilfe wir einen String in Bits konvertieren und die Bits nacheinander zählen können:
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
Bei der Initialisierung geben wir die Klassenbinärdaten an und lesen sie dann mit
GetBitund GetBitN.
Dekodierung der Quantisierungstabelle
Der Abschnitt Quantisierungstabelle definieren enthält die folgenden Daten:
| Feld | Die Größe | Beschreibung |
|---|---|---|
| Marker ID | 2 Bytes | 0xff und 0xdb identifizieren den DQT-Abschnitt |
| Länge | 2 Bytes | Länge der Quantisierungstabelle |
| Quantisierungsinformationen | 1 Byte | Bits 0 ... 3: Anzahl der Quantisierungstabellen (0 ... 3, sonst Fehler) Bits 4 ... 7: Genauigkeit der Quantisierungstabelle, 0 = 8 Bits, sonst 16 Bits |
| Bytes | n Bytes | Quantisierungstabellenwerte, n = 64 * (Genauigkeit + 1) |
Gemäß dem JPEG-Standard verfügt ein Standard-JPEG-Bild über zwei Quantisierungstabellen: für Luma und Chroma. Sie beginnen mit einem Marker
0xffdb. Das Ergebnis unseres Codes enthält bereits zwei solche Marker. Fügen wir die Möglichkeit hinzu, Quantisierungstabellen zu decodieren:
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Wir haben zuerst eine Methode definiert
GetArray. Es ist nur eine bequeme Technik zum Decodieren einer variablen Anzahl von Bytes aus Binärdaten. Wir haben auch einen Teil des Codes in der Methode ersetzt decodeHuffman, um die neue Funktion zu nutzen. Dann wurde die Methode definiert DefineQuantizationTables: Sie liest den Titel des Abschnitts mit Quantisierungstabellen und wendet dann die Quantisierungsdaten auf das Wörterbuch an, wobei der Wert des Headers als Schlüssel verwendet wird. Dieser Wert kann 0 für die Luminanz und 1 für die Chromatizität sein. Jeder Abschnitt mit Quantisierungstabellen in JFIF enthält 64 Datenbytes (für eine 8x8-Quantisierungsmatrix).
Wenn wir die Quantisierungsmatrizen für unser Bild ausgeben, erhalten wir Folgendes:
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
Dekodierung des Frame-Starts
Der Abschnitt Start of Frame enthält die folgenden Informationen ( Quelle ):
| Feld | Die Größe | Beschreibung |
|---|---|---|
| Marker ID | 2 Bytes | 0xff 0xc0 SOF |
| 2 | 8 + *3 | |
| 1 | , 8 (12 16 ). | |
| 2 | > 0 | |
| 2 | > 0 | |
| 1 | 1 = , 3 = YcbCr YIQ | |
| 3 | 3 . (1 ) (1 = Y, 2 = Cb, 3 = Cr, 4 = I, 5 = Q), (1 ) ( 0...3 , 4...7 ), (1 ). |
Hier interessiert uns nicht alles. Wir werden die Breite und Höhe des Bildes sowie die Anzahl der Quantisierungstabellen für jede Komponente extrahieren. Die Breite und Höhe werden verwendet, um die Dekodierung der tatsächlichen Scans des Bildes im Abschnitt "Start des Scans" zu starten. Da wir hauptsächlich mit einem YCbCr-Bild arbeiten, können wir davon ausgehen, dass es drei Komponenten gibt und deren Typen 1, 2 bzw. 3 sind. Schreiben wir den Code, um diese Daten zu dekodieren:
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Wir haben der JPEG-Klasse
quantMappingein BaselineDCTListenattribut hinzugefügt und eine Methode definiert , die die erforderlichen Daten aus dem SOF-Abschnitt decodiert und die Anzahl der Quantisierungstabellen für jede Komponente in die Liste einfügt quantMapping. Wir werden dies nutzen, wenn wir den Abschnitt Start des Scans lesen. So sieht es für unser Bild aus quantMapping:
Quant mapping: [0, 1, 1]
Dekodierung Start des Scans
Dies ist das "Fleisch" eines JPEG-Bildes, es enthält die Daten des Bildes selbst. Wir haben das wichtigste Stadium erreicht. Alles, was wir zuvor dekodiert haben, kann als Karte betrachtet werden, die uns hilft, das Bild selbst zu dekodieren. Dieser Abschnitt enthält das Bild selbst (codiert). Wir lesen den Abschnitt und entschlüsseln mit den bereits dekodierten Daten.
Alle Marker begannen mit
0xff. Dieser Wert kann auch Teil des gescannten Bildes sein. Wenn er jedoch in diesem Abschnitt vorhanden ist, folgt immer und 0x00. Der JPEG-Encoder fügt es automatisch ein, dies wird als Byte-Stuffing bezeichnet. Daher muss der Decoder diese entfernen 0x00. Beginnen wir mit einer SOS-Decodierungsmethode, die eine solche Funktion enthält, und entfernen die vorhandenen 0x00. In unserem Bild im Abschnitt mit einem Scan gibt es keine0xffaber es ist immer noch eine nützliche Ergänzung.
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
Früher haben wir manuell nach dem Ende der Datei gesucht, als wir einen Marker gefunden
0xffdahaben. Jetzt, da wir ein Tool haben, mit dem wir die gesamte Datei systematisch anzeigen können, verschieben wir die Markierungssuchbedingung innerhalb des Operators else. Die Funktion wird RemoveFF00nur unterbrochen, wenn etwas anderes statt 0x00nachher gefunden wird 0xff. Die Schleife wird unterbrochen, wenn die Funktion gefunden wird 0xffd9, sodass wir ohne Angst vor Überraschungen nach dem Ende der Datei suchen können. Wenn Sie diesen Code ausführen, wird im Terminal nichts Neues angezeigt.
Denken Sie daran, dass JPEG das Bild in 8x8-Matrizen aufteilt. Jetzt müssen wir die gescannten Bilddaten in einen Bitstream konvertieren und in 8x8-Blöcken verarbeiten. Fügen wir den Code unserer Klasse hinzu:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
Beginnen wir mit der Konvertierung der Daten in einen Bitstrom. Erinnern Sie sich, dass die Delta-Codierung auf das DC-Element der Quantisierungsmatrix (ihr erstes Element) relativ zum vorherigen DC-Element angewendet wird? Daher initialisieren wir
oldlumdccoeff, oldCbdccoeffund oldCrdccoeffmit Null - Werten, werden sie uns helfen , den Überblick über den Wert der vorherigen DC - Elemente und 0 standardmäßig eingestellt werden , wenn wir das erste DC - Element finden.
Die Schleife
formag seltsam erscheinen. self.height//8sagt uns, wie oft wir die Höhe durch 8 8 teilen können, und es ist dasselbe mit der Breite und self.width//8.
BuildMatrixnimmt eine Quantisierungstabelle und fügt Parameter hinzu, erstellt eine inverse diskrete Cosinustransformationsmatrix und gibt uns die Y-, Cr- und Cb-Matrizen. Und die Funktion DrawMatrixkonvertiert sie in RGB.
Zuerst erstellen wir eine Klasse
IDCTund beginnen Sie dann, die Methode auszufüllen BuildMatrix.
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
Lassen Sie uns die Klasse analysieren
IDCT. Wenn wir die MCU extrahieren, wird sie in einem Attribut gespeichert base. Dann transformieren wir die MCU-Matrix, indem wir den Zick-Zack-Scan mit der Methode zurücksetzen rearrange_using_zigzag. Schließlich werden wir die diskrete Cosinustransformation durch Aufrufen der Methode zurücksetzen perform_IDCT.
Wie Sie sich erinnern, ist die DC-Tabelle fest. Wir werden nicht überlegen, wie DCT funktioniert, dies hängt mehr mit Mathematik als mit Programmierung zusammen. Wir können diese Tabelle als globale Variable speichern und nach Wertepaaren abfragen
x,y. Ich beschloss, die Tabelle und ihre Berechnung in eine Klasse einzuteilen IDCT, um den Text lesbar zu machen. Jedes Element der transformierten MCU-Matrix wird mit einem Wert multipliziert idc_variableund wir erhalten die Y-, Cr- und Cb-Werte.
Dies wird klarer, wenn wir die Methode hinzufügen
BuildMatrix.
Wenn Sie die Zick-Zack-Tabelle so ändern, dass sie folgendermaßen aussieht:
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
Sie erhalten dieses Ergebnis (beachten Sie die kleinen Artefakte):

Und wenn Sie den Mut haben, können Sie die Zick-Zack-Tabelle noch weiter modifizieren:
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
Dann wird das Ergebnis so aussehen:

Vervollständigen wir unsere Methode
BuildMatrix:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
Wir beginnen mit der Erstellung einer diskreten Cosinustransformations-Invertierungsklasse (
IDCT()). Dann lesen wir die Daten in den Bitstrom und decodieren sie mit einer Huffman-Tabelle.
self.huffman_tables[0]und self.huffman_tables[1]beziehen sich auf DC-Tabellen für Luma bzw. Chroma self.huffman_tables[16]und self.huffman_tables[17]auf AC-Tabellen für Luma bzw. Chroma.
Nach dem Decodieren des Bitstroms verwenden wir eine Funktion,
DecodeNumber um den neuen Delta-codierten DC-Koeffizienten zu extrahieren und zu addieren olddccoefficient, um den Delta-decodierten DC-Koeffizienten zu erhalten.
Dann wiederholen wir das gleiche Decodierungsverfahren mit den AC-Werten in der Quantisierungsmatrix. Code Bedeutung
0zeigt an, dass wir die EOB-Markierung (End of Block) erreicht haben und anhalten müssen. Darüber hinaus gibt der erste Teil der AC-Quantisierungstabelle an, wie viele führende Nullen wir haben. Denken wir nun daran, die Längen der Serie zu codieren. Lassen Sie uns diesen Prozess umkehren und all diese vielen Bits überspringen. IDCTIhnen werden in der Klasse explizit Nullen zugewiesen.
Nach dem Decodieren der DC- und AC-Werte für die MCU konvertieren wir die MCU und invertieren den Zick-Zack-Scan durch Aufrufen
rearrange_using_zigzag. Und dann invertieren wir die DCT und wenden sie auf die decodierte MCU an.
Die Methode
BuildMatrixgibt die invertierte DCT-Matrix und den Wert des DC-Koeffizienten zurück. Denken Sie daran, dass dies eine Matrix für nur eine minimale 8x8-Codiereinheit ist. Lassen Sie uns dies für alle anderen MCUs in unserer Datei tun.
Anzeigen eines Bildes auf dem Bildschirm
Lassen Sie uns nun unseren Code in der Methode dazu bringen
StartOfScan, einen Tkinter-Canvas zu erstellen und jede MCU nach dem Decodieren zu zeichnen.
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
Beginnen wir mit Funktionen
ColorConversionund Clamp. ColorConversionNimmt Y-, Cr- und Cb-Werte, konvertiert sie nach der Formel in RGB-Komponenten und gibt dann die aggregierten RGB-Werte aus. Warum 128 hinzufügen, könnte man fragen? Denken Sie daran, dass vor dem JPEG-Algorithmus DCT auf die MCU angewendet wird und 128 von den Farbwerten subtrahiert. Wenn die Farben ursprünglich im Bereich [0,255] lagen, werden sie von JPEG in den Bereich [-128, + 128] verschoben. Wir müssen diesen Effekt beim Decodieren zurücksetzen, also fügen wir RGB 128 hinzu. Was Clamp, beim Auspacken können die resultierenden Werte außerhalb des Bereichs gehen [0.255], so dass wir sie in diesem Bereich zu halten [0.255].
In Methode
DrawMatrixWir durchlaufen jede decodierte 8x8-Matrix für Y, Cr und Cb und konvertieren jedes Matrixelement in RGB-Werte. Nach der Transformation zeichnen wir canvasmit der Methode Pixel in Tkinter create_rectangle. Sie finden den gesamten Code auf GitHub . Wenn Sie es ausführen, wird mein Gesicht auf dem Bildschirm angezeigt.
Fazit
Wer hätte gedacht, dass man, um mein Gesicht zu zeigen, eine Erklärung mit mehr als 6.000 Wörtern schreiben müsste. Es ist erstaunlich, wie klug die Autoren einiger Algorithmen waren! Ich hoffe, Ihnen hat der Artikel gefallen. Ich habe beim Schreiben dieses Decoders viel gelernt. Ich dachte nicht, dass das Codieren eines einfachen JPEG-Bildes so viel Mathematik erfordert. Das nächste Mal können Sie versuchen, einen Decoder für PNG (oder ein anderes Format) zu schreiben.
Zusätzliche Materialien
Wenn Sie an den Details interessiert sind, lesen Sie die Materialien, mit denen ich den Artikel geschrieben habe, sowie einige zusätzliche Arbeiten:
- Illustrierte Anleitung zum Enträtseln von JPEG
- Ein sehr detaillierter Artikel über die Huffman-Codierung in JPEG
- Schreiben einer einfachen JPEG-Bibliothek in C ++
- Dokumentation für struct in Python 3
- Wie FB das JPEG-Wissen nutzte
- JPEG-Layout und Format
- Interessante DoD-Präsentation zur JPEG-Forensik