Wir verstehen und schaffen
Die gute Nachricht vor dem Artikel: Zum Lesen und (hoffentlich!) Verstehen sind keine hohen mathematischen Fähigkeiten erforderlich.
Haftungsausschluss: Der Codeteil dieses Artikels ist wie der vorherige eine angepasste, ergänzte und getestete Übersetzung. Ich bin dem Autor dankbar, denn dies ist eine meiner ersten Erfahrungen im Code, nach der ich noch mehr überflutet habe. Ich hoffe, dass meine Anpassung für Sie genauso funktioniert!
So lass uns gehen!
Die Struktur ist wie folgt:
- Was ist eine Markov-Kette?
- Ein Beispiel für die Funktionsweise der Kette
- Übergangsmatrix
- Markov-Kettenmodell mit Python - datengesteuerte Texterzeugung
Was ist eine Markov-Kette?
Die Markov-Kette ist ein Werkzeug aus der Theorie der Zufallsprozesse, das aus einer Folge von n Zuständen besteht. In diesem Fall werden Verbindungen zwischen Knoten (Werten) der Kette nur hergestellt, wenn die Zustände streng nebeneinander liegen.
Lassen Sie uns unter Berücksichtigung des fetten Wortes nur die Eigenschaft der Markov-Kette ableiten: Die
Wahrscheinlichkeit eines bestimmten neuen Zustands in der Kette hängt nur vom gegenwärtigen Zustand ab und berücksichtigt mathematisch nicht die Erfahrung vergangener Zustände => Eine Markov-Kette ist eine Kette ohne Gedächtnis.
Mit anderen Worten, eine neue Bedeutung tanzt immer von der, die sie direkt am Griff hält.
Ein Beispiel für die Funktionsweise der Kette
Nehmen wir wie der Autor des Artikels, aus dem die Code-Implementierung entlehnt ist, eine zufällige Folge von Wörtern.
Start - künstlich - Pelzmantel - künstlich - Essen - künstlich - Pasta - künstlich - Pelzmantel - künstlich - Ende
Stellen wir uns vor, dass dies tatsächlich ein großartiger Vers ist und unsere Aufgabe darin besteht, den Stil des Autors zu kopieren. (Aber dies zu tun ist natürlich unethisch)
Wie entscheide ich mich?
Das erste, was ich tun möchte, ist, die Häufigkeit von Wörtern zu zählen (wenn wir dies mit einem Live-Text tun würden, wäre es zunächst sinnvoll, eine Normalisierung durchzuführen - jedes Wort in ein Lemma zu bringen (Wörterbuchform)).
Start == 1
Künstlich == 5
Pelzmantel == 2
Nudeln == 1
Essen == 1
Ende == 1
Wenn wir bedenken, dass wir eine Markov-Kette haben, können wir die Verteilung neuer Wörter in Abhängigkeit von den vorherigen grafisch darstellen:

Verbal:
- Der Zustand von Pelzmantel, Nahrung und Nudeln zu 100% beinhaltet den Zustand von künstlichem p = 1
- Der „künstliche“ Zustand kann mit gleicher Wahrscheinlichkeit zu 4 Zuständen führen, und die Wahrscheinlichkeit, in den Zustand eines künstlichen Pelzmantels zu gelangen, ist höher als bei den anderen drei
- Endzustand führt nirgendwo hin
- Der Zustand "Start" 100% beinhaltet den Zustand "künstlich".
Es sieht cool und logisch aus, aber die visuelle Schönheit hört hier nicht auf! Wir können auch eine Übergangsmatrix konstruieren und auf ihrer Grundlage mit der folgenden mathematischen Gerechtigkeit appellieren:

Was bedeutet auf Russisch „die Summe einer Reihe von Wahrscheinlichkeiten für ein bestimmtes Ereignis k, abhängig von i == die Summe aller Werte der Wahrscheinlichkeiten des Ereignisses k, abhängig vom Auftreten des Zustands i, wobei Ereignis k == m + 1 und Ereignis i == m (dh Ereignis k unterscheidet sich immer um eins von i) ".
Aber zuerst wollen wir verstehen, was eine Matrix ist.
Übergangsmatrix
Bei der Arbeit mit Markov-Ketten handelt es sich um eine stochastische Übergangsmatrix - eine Reihe von Vektoren, in denen die Werte die Werte der Wahrscheinlichkeiten zwischen Abstufungen widerspiegeln.
Ja, ja, es klingt wie es klingt.
Aber es sieht nicht so beängstigend aus:

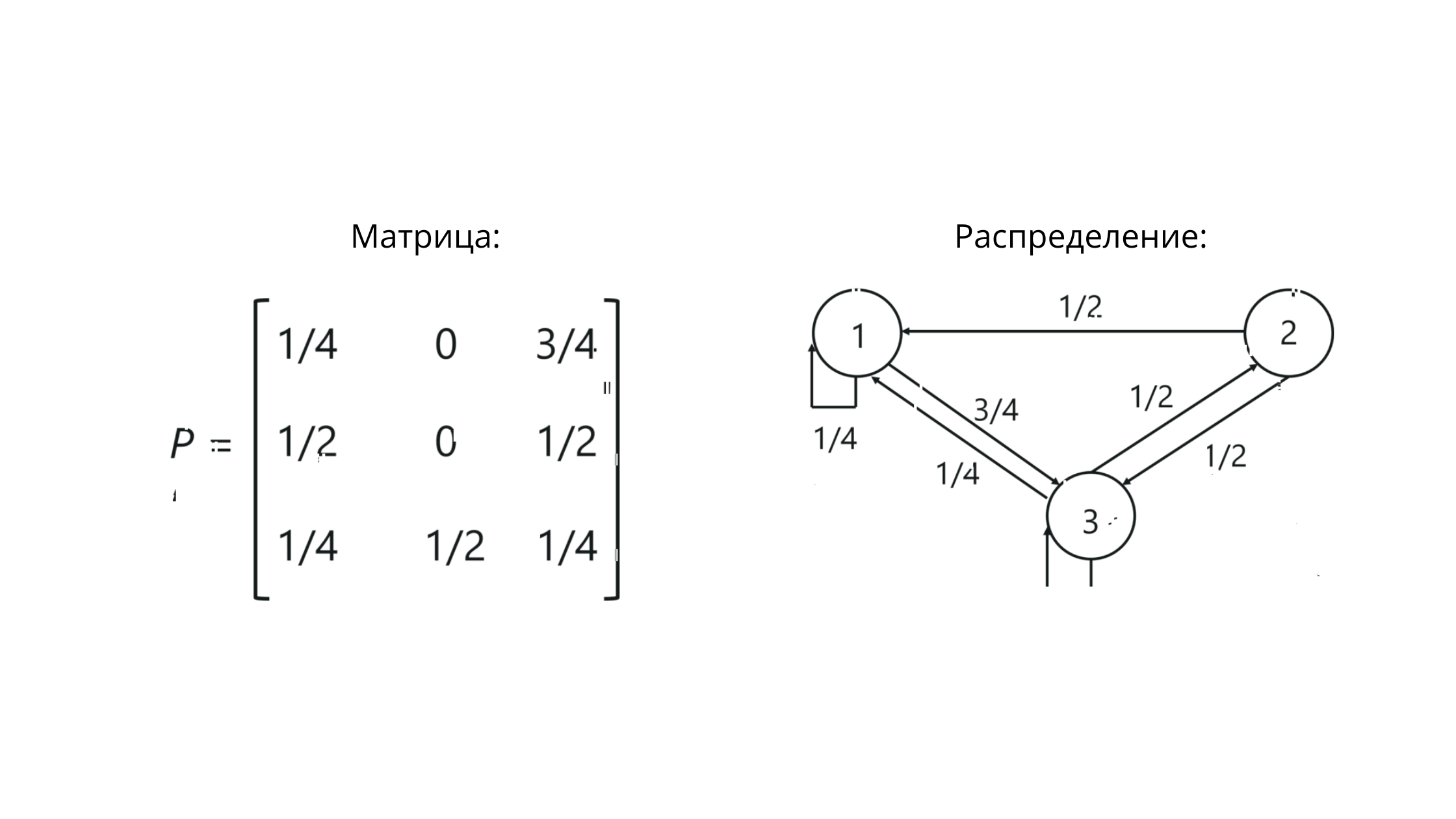
P ist die Notation für eine Matrix. Die Werte am Schnittpunkt von Spalten und Zeilen spiegeln hier die Wahrscheinlichkeiten von Übergängen zwischen Zuständen wider.
In unserem Beispiel sieht es ungefähr so aus:

Beachten Sie, dass die Summe der Werte in der Zeile == 1 ist. Dies bedeutet, dass wir alles korrekt erstellt haben, da die Summe der Werte in der Zeile der stochastischen Matrix gleich eins sein muss.
Nacktes Beispiel ohne Kunstpelzmäntel und Pasten: Ein
noch nacktes Beispiel ist die Identitätsmatrix für:
- der Fall, wenn es unmöglich ist, von A zurück nach B und von B - zurück nach A zu gehen [1]
- der Fall, wenn der Übergang von A nach B zurück möglich ist [2]

Respekt. Mit der Theorie fertig.
Wir verwenden Python.
Ein Modell basierend auf der Markov-Kette mit Python - Generieren von Text basierend auf Daten
Schritt 1
Importieren Sie das entsprechende Paket für die Arbeit und rufen Sie die Daten ab.
import numpy as np
data = open('/Users/sad__sabrina/Desktop/1.txt', encoding='utf8').read()
print(data)
, , , , ( « memorylessness »). , , , , , , ; .., , .
Konzentrieren Sie sich nicht auf die Struktur des Textes, sondern achten Sie auf die utf8-Codierung. Dies ist wichtig zum Lesen der Daten.
Schritt 2
Teilen Sie die Daten in Wörter.
ind_words = data.split()
print(ind_words)
['\ufeff', '', '', '', '', ',', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', ',', '', '', '', '', '(', '', '', '«', 'memorylessness', '»).', '', ',', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', ',', '', '', '', ';', '..,', '', '', '', '', ',', '', '', '', '', '', '', '.']Schritt 3
Erstellen Sie eine Funktion zum Verknüpfen von Wortpaaren.
def make_pairs(ind_words):
for i in range(len(ind_words) - 1):
yield (ind_words[i], ind_words[i + 1])
pair = make_pairs(ind_words)Die Hauptnuance der Funktion bei der Verwendung des Operatorsield (). Es hilft uns, das Markov-Verkettungskriterium zu erfüllen - das speicherlose Speicherkriterium. Mit Yield erstellt unsere Funktion neue Paare, wenn sie iteriert (Wiederholungen), anstatt alles zu speichern.
Hier kann es zu Missverständnissen kommen, weil aus einem Wort ein anderes werden kann. Wir werden dieses Problem lösen, indem wir ein Wörterbuch für unsere Funktion erstellen.
Schritt 4
word_dict = {}
for word_1, word_2 in pair:
if word_1 in word_dict.keys():
word_dict[word_1].append(word_2)
else:
word_dict[word_1] = [word_2]Hier:
- Wenn wir bereits einen Eintrag über das erste Wort in einem Paar im Wörterbuch haben, fügt die Funktion der Liste den nächsten potenziellen Wert hinzu.
- Andernfalls wird ein neuer Eintrag erstellt.
Schritt 5
Lassen Sie uns das erste Wort zufällig auswählen und, um das Wort wirklich zufällig zu machen, die while-Bedingung mithilfe der Zeichenfolgenmethode islower () festlegen, die True erfüllt, wenn die Zeichenfolge Kleinbuchstaben enthält und das Vorhandensein von Zahlen oder Symbolen zulässt.
In diesem Fall setzen wir die Anzahl der Wörter auf 20.
first_word = np.random.choice(ind_words)
while first_word.islower():
chain = [first_word]
n_words = 20
first_word = np.random.choice(ind_words)
for i in range(n_words):
chain.append(np.random.choice(word_dict[chain[-1]]))Schritt 6
Beginnen wir mit unserer zufälligen Sache!
print(' '.join(chain))
; .., , , (Die Funktion join () ist eine Funktion zum Arbeiten mit Zeichenfolgen. In Klammern haben wir ein Trennzeichen für Werte in der Zeile (Leerzeichen) angegeben.
Und der Text ... nun, es klingt maschinenartig und fast logisch.
PS Wie Sie vielleicht bemerkt haben, sind Markov-Ketten in der Linguistik nützlich, aber ihre Anwendung geht über die Verarbeitung natürlicher Sprache hinaus. Hier und hier können Sie sich mit der Verwendung von Ketten bei anderen Aufgaben vertraut machen.
PPS Wenn sich herausstellt, dass meine Code-Praxis für Sie unverständlich ist, füge ich den Originalartikel bei . Stellen Sie sicher, dass Sie den Code in der Praxis anwenden - das Gefühl, wenn er "ausgeführt und generiert" wird, wird aufgeladen!
Ich warte auf Ihre Meinung und freue mich über konstruktive Kommentare zu dem Artikel!