Clever Geek Handbook

Das Geburtstagsparadoxon bei VK-Daten

Hallo!



Ich habe beschlossen, das Geburtstagsparadoxon anhand von Daten zu überprüfen, die von VK verfügbar sind.



Was ist das Geburtstagsparadoxon?



Versuchen Sie, die Frage zu beantworten: Wie viele Personen in einem Raum werden benötigt, damit zwei Personen mit einer Wahrscheinlichkeit von 0,5 denselben Geburtstag haben? (Datum und Monat). Das Geburtstagsparadoxon beantwortet diese Frage.



Um das Problem zu lösen, sollten einige Voraussetzungen hervorgehoben werden:



  1. Das Modell hat keinen 29. Februar => 365 Tage im Jahr im Modell
  2. Jeder der 365 Tage ist gleich wahrscheinlich.


Natürlich ist es nicht ganz realistisch, dass Geburtstage gleichermaßen wahrscheinlich sind - es gibt saisonale Effekte, die sich auf das Geburtsdatum von Kindern auswirken. Ich denke, Sie können selbst erraten, welche ...



Die meisten Menschen beantworten die Frage des Problems intuitiv: 180. Sieht logisch aus, 180 Menschen werden benötigt, um zu haben Wahrscheinlichkeit von 0,5 identischen Geburtstagen (insgesamt 365 Tage). Jeder, der noch nie von dem Geburtstagsparadoxon gehört hat, handelt von dieser Intuition. Die richtige Antwort ist tatsächlich viel weniger als 180 und sogar 150 und sogar 100: 23.



Mindestens 1 passender Geburtstag ist erforderlich - damit ich die Wahrscheinlichkeit ermitteln kann, dass es keine passenden Geburtstage gibt:

P(" ")=365∗364∗363∗...∗(365−k+1)365k=365!365k∗(365−k)!

.

Die Idee ist folgende: Ich nehme die erste Person und erinnere mich an ihren Geburtstag, dann die zweite und berechne die Wahrscheinlichkeit, dass sein Geburtstag nicht mit dem Geburtstag der ersten übereinstimmt; weiter als der dritte und ich berechne die Wahrscheinlichkeit, dass sein Geburtstag nicht mit den Geburtstagen des ersten und zweiten übereinstimmt.



Wenn man die Gleichung löst, stellt sich heraus, dass 23 Personen benötigt werden und die Wahrscheinlichkeit, dass Geburtstage zusammenfallen, 0,5073 beträgt, bei 100 Personen beträgt die Wahrscheinlichkeit 0,9999.



Sehen wir uns das Paradoxon bei VK-Daten an.



Theoretisch beträgt bei 23 Personen die Wahrscheinlichkeit, dass Geburtstage zusammenfallen, 0,5073, bei 50 Personen 0,97 und bei 100 0,99. Lassen Sie es uns über die VK-API überprüfen.



1. Ich wähle eine große Community in VK. Ich habe mich entschieden, die MDK-Gruppe auf Vkontakte zu übernehmen ...



Zuerst erstelle ich eine CSV-Datei mit den Spalten, die ich benötige. 



with open('vk_data.csv', 'w') as new_file:
                # csv
                fieldnames = ['id', 'bdate', 'bmonth', 'byear', 'dandm']

                csv_writer = csv.DictWriter(new_file, fieldnames=fieldnames, delimiter=',')

                csv_writer.writeheader()

                newDict = dict()


Ich melde mich über die API bei VK an und stelle die Öffentlichkeit ein, die ich brauche 

vk_session = vk_api.VkApi('username', 'password')
                vk_session.auth()

                vk = vk_session.get_api()
                
                vk_group = vk.groups.getMembers(group_id = 'mudakoff', fields = 'bdate')


Wir beginnen mit dem Parsen von VKontakte. Mit der API können Sie nur 1000 Benutzer analysieren. Daher erstelle ich eine Schleife. 



for i in range(0, 20):
                    vk_group = vk.groups.getMembers(group_id = 'mudakoff', offset = 1000 * i,  fields = 'bdate')
                    for k in range(0, 1000):
                        try:
                            new_file.write(str(vk_group['items'][k]["id"]) + ',' + str(vk_group['items'][k]["bdate"]).replace('.', ','))
                            new_file.write('\n')
                        except:
                            pass


Theoretisch haben wir angenommen, dass Geburtstage genauso wahrscheinlich sind, aber was passiert in der Praxis? Ich werde ein Histogramm der Geburtstage erstellen.



Bild



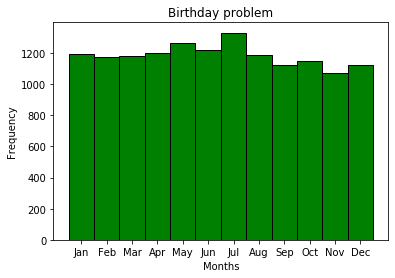
Geburtstage pro Monat sind keine gleichwahrscheinlichen Ereignisse, was im Allgemeinen durchaus logisch ist - dies ist nur eine Voraussetzung für die Lösung des Geburtstagsproblems. Offensichtlich wird es verschiedene saisonale Ereignisse für verschiedene Orte geben. Aus irgendeinem Grund ist der Juli der beliebteste Monat zum Geburtstag von MDK-Abonnenten.



Ich werde empirisch die Wahrscheinlichkeit abschätzen, dass es in einer Gruppe von 50 willkürlichen Personen mindestens zwei mit demselben Geburtstag gibt. Zu diesem Zweck habe ich einen Zyklus geschrieben, in dem eine Teilstichprobe von 50 Zeilen aus der Tabelle auftritt. Für diese 50 Zeilen innerhalb des Zustands habe ich die Übereinstimmung der Geburtstage überprüft. Wenn es übereinstimmte, erinnerte ich mich an die Zählervariable, die ich anschließend durch die Zykluslänge dividiere, um die Wahrscheinlichkeit zu erhalten. 



fifty = df["dandm"].sample(n = 50)
for i in range(0, 1000):
    fifty = df["dandm"].sample(n = 50)
    for j in fifty.duplicated():
        if j == True:
            counter = counter + 1
            break
print(':', counter / 1000)


Die Wahrscheinlichkeit wird im Bereich von 0,97 erhalten, was mit den theoretischen Daten übereinstimmt.



Ausgabe



Es war interessant zu sehen, wie sich die Theorie auf den Empirismus bezieht, und in diesem Fall bestätigen die Daten die Theorie. Es ist zu beachten, dass das Ergebnis repräsentativ ist, da die Stichprobe groß genug ist - 20.000 Personen.



Ressourcen



  1. Harvard Universität. Geburtstagsproblem, Wahrscheinlichkeitseigenschaften | Statistik 110. URL: www.youtube.com/watch?v=LZ5Wergp_PA&t=150s . Zugriff: 07.08.2020
  2. Geburtstagsproblem. URL: en.wikipedia.org/wiki/Birthday_problem . Zugriff: 07.08.2020>


More articles:


All Articles