Gepanzerte Kriegsführung: Projekt Armata. Chromatische Abweichung

Armored Warfare: Project Armata ist ein kostenloses Online-Panzer-Action-Spiel, das vom Allods Team, dem Spielestudio MY.GAMES, entwickelt wurde. Trotz der Tatsache, dass das Spiel auf CryEngine erstellt wurde, einer ziemlich beliebten Engine mit einem guten Echtzeit-Rendering, müssen wir für unser Spiel viel von Grund auf neu modifizieren und erstellen. In diesem Artikel möchte ich darüber sprechen, wie wir die chromatische Aberration für die Ansicht der ersten Person implementiert haben und was es ist.

Was ist chromatische Aberration?

Chromatische Aberration ist ein Linsenfehler, bei dem nicht alle Farben am gleichen Punkt ankommen. Dies liegt daran, dass der Brechungsindex des Mediums von der Wellenlänge des Lichts abhängt (siehe Dispersion ). So sieht beispielsweise die Situation aus, wenn das Objektiv nicht unter chromatischer Aberration leidet:





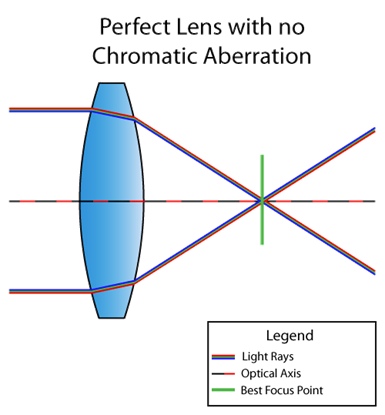
Und hier ist ein Objektiv mit einem Defekt:





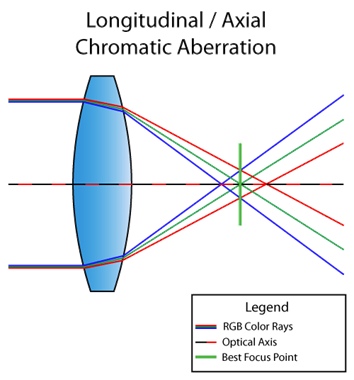
Die obige Situation wird übrigens als longitudinale (oder axiale) chromatische Aberration bezeichnet. Es tritt auf, wenn verschiedene Wellenlängen nach dem Passieren der Linse nicht am gleichen Punkt in der Brennebene konvergieren. Dann ist der Defekt im ganzen Bild sichtbar:





Im Bild oben sehen Sie, dass lila und grüne Farben aufgrund eines Defekts hervorstechen. Kann nicht sehen? Und auf diesem Bild?





Es gibt auch eine laterale (oder laterale) chromatische Aberration. Es tritt auf, wenn Licht in einem Winkel zur Linse einfällt. Infolgedessen konvergieren unterschiedliche Wellenlängen des Lichts an unterschiedlichen Punkten in der Brennebene. Hier ist ein Bild, das Sie verstehen sollten:





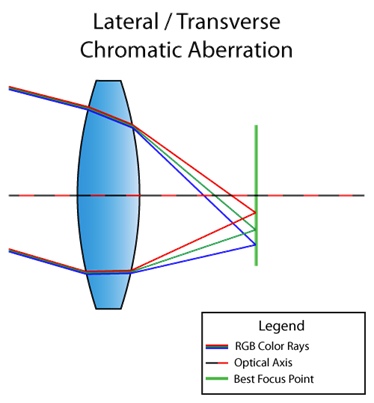
Sie können bereits aus dem Diagramm ersehen, dass wir dadurch eine vollständige Zerlegung des Lichts von rot nach violett erhalten. Im Gegensatz zur Längsrichtung tritt die laterale chromatische Aberration niemals in der Mitte auf, sondern nur näher an den Bildrändern. Damit Sie verstehen, was ich meine, hier ein weiteres Bild aus dem Internet:





Nun, da wir mit der Theorie fertig sind, kommen wir zum Punkt.

Seitliche chromatische Aberration mit leichter Zersetzung

Ich beginne mit der Tatsache, dass ich die Frage beantworten werde, die sich im Kopf vieler von Ihnen stellen könnte: "Ist CryEngine nicht eine chromatische Aberration implementiert?" Es gibt. Es wird jedoch in der Nachbearbeitungsphase im selben Shader mit Schärfen verwendet, und der Algorithmus sieht folgendermaßen aus ( Link zum Code ):

screenColor.r = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 + 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).r;
screenColor.b = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 - 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).b;

Was im Prinzip funktioniert. Aber wir haben ein Spiel über Panzer. Wir brauchen diesen Effekt nur für die Ansicht der ersten Person und nur für die Schönheit, das heißt, damit alles in der Mitte im Fokus steht (Hallo zur lateralen Aberration). Daher entsprach die aktuelle Implementierung zumindest nicht der Tatsache, dass ihre Wirkung im gesamten Bild sichtbar war.



So sah die Aberration selbst aus (Aufmerksamkeit auf die linke Seite):





Und so sah es aus, wenn Sie die Parameter verdrehen:





Deshalb haben wir uns zum Ziel gesetzt:

1. Implementieren Sie eine laterale chromatische Aberration, so dass in der Nähe des Oszilloskops alles scharfgestellt ist. Wenn an den Seiten keine charakteristischen Farbfehler sichtbar sind, müssen Sie diese zumindest verwischen.
2. Abtasten einer Textur durch Multiplizieren von RGB-Kanälen mit Koeffizienten, die einer bestimmten Wellenlänge entsprechen. Ich habe noch nicht darüber gesprochen, daher ist jetzt möglicherweise nicht ganz klar, worum es in diesem Punkt geht. Aber wir werden es später definitiv in allen Details betrachten.

Schauen wir uns zunächst den allgemeinen Mechanismus und den Code zur Erzeugung der lateralen chromatischen Aberration an.

half distanceStrength = pow(length(IN.baseTC - 0.5), falloff);
half2 direction = normalize(IN.baseTC.xy - 0.5);
half2 velocity = direction * blur * distanceStrength;

Also wird zuerst eine kreisförmige Maske erstellt, die für den Abstand von der Mitte des Bildschirms verantwortlich ist, dann wird die Richtung von der Mitte des Bildschirms berechnet und dann wird all dies mit multipliziert blur. Blurund falloff- dies sind Parameter, die von außen übergeben werden und nur Multiplikatoren zum Einstellen der Aberration sind. Außerdem wird von außen ein Parameter geworfen sampleCount, der nicht nur für die Anzahl der Abtastwerte verantwortlich ist, sondern tatsächlich auch für den Schritt zwischen den Abtastpunkten

half2 offsetDecrement = velocity * stepMultiplier / half(sampleCount);

Jetzt müssen wir nur noch sampleCounteinmal von einem bestimmten Punkt der Textur gehen und uns jedes Mal verschieben offsetDecrement, die Kanäle mit den entsprechenden Wellengewichten multiplizieren und durch die Summe dieser Gewichte dividieren. Nun, es ist Zeit, über den zweiten Punkt unseres globalen Ziels zu sprechen.



Das sichtbare Lichtspektrum reicht von 380 nm (violett) bis 780 nm (rot). Und siehe da, die Wellenlänge kann in eine RGB-Palette konvertiert werden. In Python sieht der Code, der diese Magie ausführt, folgendermaßen aus:

def get_color(waveLength):
    if waveLength >= 380 and waveLength < 440:
        red = -(waveLength - 440.0) / (440.0 - 380.0)
        green = 0.0
        blue  = 1.0
    elif waveLength >= 440 and waveLength < 490:
        red   = 0.0
        green = (waveLength - 440.0) / (490.0 - 440.0)
        blue  = 1.0
    elif waveLength >= 490 and waveLength < 510:
        red   = 0.0
        green = 1.0
        blue  = -(waveLength - 510.0) / (510.0 - 490.0)
    elif waveLength >= 510 and waveLength < 580:
        red   = (waveLength - 510.0) / (580.0 - 510.0)
        green = 1.0
        blue  = 0.0
    elif waveLength >= 580 and waveLength < 645:
        red   = 1.0
        green = -(waveLength - 645.0) / (645.0 - 580.0)
        blue  = 0.0
    elif waveLength >= 645 and waveLength < 781:
        red   = 1.0
        green = 0.0
        blue  = 0.0
    else:
        red   = 0.0
        green = 0.0
        blue  = 0.0
    
    factor = 0.0
    if waveLength >= 380 and waveLength < 420:
        factor = 0.3 + 0.7*(waveLength - 380.0) / (420.0 - 380.0)
    elif waveLength >= 420 and waveLength < 701:
        factor = 1.0
    elif waveLength >= 701 and waveLength < 781:
        factor = 0.3 + 0.7*(780.0 - waveLength) / (780.0 - 700.0)
 
    gamma = 0.80
    R = (red   * factor)**gamma if red > 0 else 0
    G = (green * factor)**gamma if green > 0 else 0
    B = (blue  * factor)**gamma if blue > 0 else 0
    
    return R, G, B

Als Ergebnis erhalten wir folgende Farbverteilung:





Kurz gesagt, die Grafik zeigt, wie viel und welche Farbe in einer Welle mit einer bestimmten Länge enthalten ist. Auf der Ordinatenachse erhalten wir nur die gleichen Gewichte, über die ich zuvor gesprochen habe. Jetzt können wir den Algorithmus unter Berücksichtigung der zuvor genannten Punkte vollständig implementieren:

half3 accumulator = (half3) 0;
half2 offset = (half2) 0;
half3 WeightSum = (half3) 0;
half3 Weight = (half3) 0;
half3 color;
half waveLength;
 
for (int i = 0; i < sampleCount; i++)
{
    waveLength = lerp(startWaveLength, endWaveLength, (half)(i) / (sampleCount - 1.0));
    Weight.r = GetRedWeight(waveLength);
    Weight.g = GetGreenWeight(waveLength);
    Weight.b = GetBlueWeight(waveLength);
        
    offset -= offsetDecrement;
        
    color = tex2Dlod(baseMap, half4(IN.baseTC + offset, 0, 0)).rgb;
    accumulator.rgb += color.rgb * Weight.rgb; 
        
    WeightSum.rgb += Weight.rgb;
}
 
OUT.Color.rgb = half4(accumulator.rgb / WeightSum.rgb, 1.0);

Das heißt, je mehr wir haben sampleCount, desto weniger Schritt haben wir zwischen den Abtastpunkten und desto mehr streuen wir das Licht (wir berücksichtigen mehr Wellen mit unterschiedlichen Längen).



Wenn es immer noch nicht klar ist, dann schauen sie sich an einem konkreten Beispiel, nämlich unseren ersten Versuch, und ich werde erklären , was zu nehmen startWaveLengthund endWaveLength, und , wie die Funktionen umgesetzt werden GetRed(Green, Blue)Weight.

Anpassung des gesamten sichtbaren Spektrums

Aus der obigen Grafik kennen wir das ungefähre Verhältnis und die ungefähren Werte der RGB-Palette für jede Wellenlänge. Zum Beispiel sehen wir für eine Wellenlänge von 380 nm (violett) (siehe das gleiche Diagramm), dass RGB (0,4, 0, 0,4). Es sind diese Werte, die wir für die Gewichte nehmen, über die ich zuvor gesprochen habe.



Versuchen wir nun, die Funktion, Farbe durch ein Polynom vierten Grades zu erhalten, loszuwerden, damit die Berechnungen billiger sind (wir sind kein Pixar-Studio, sondern ein Spielestudio: Je billiger die Berechnungen, desto besser). Dieses Polynom vierten Grades sollte sich den resultierenden Graphen annähern. Um das Polynom zu erstellen, habe ich die SciPy-Bibliothek verwendet:

wave_arange = numpy.arange(380, 780, 0.001)
red_func = numpy.polynomial.polynomial.Polynomial.fit(wave_arange, red, 4)

Als Ergebnis wird das folgende Ergebnis erhalten (ich habe in 3 separate Diagramme aufgeteilt, die jedem separaten Kanal entsprechen, damit es einfacher ist, mit dem genauen Wert zu vergleichen):









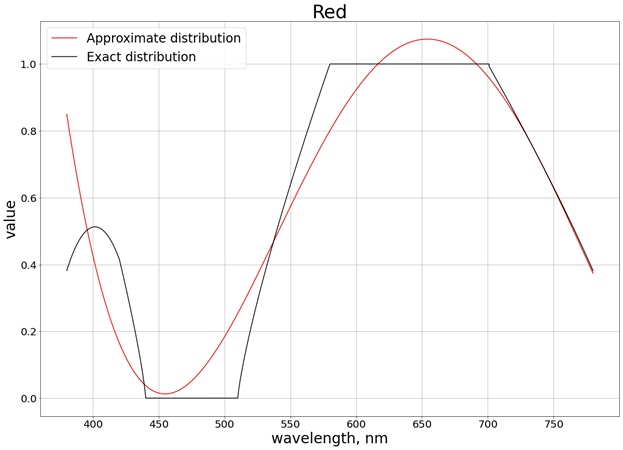
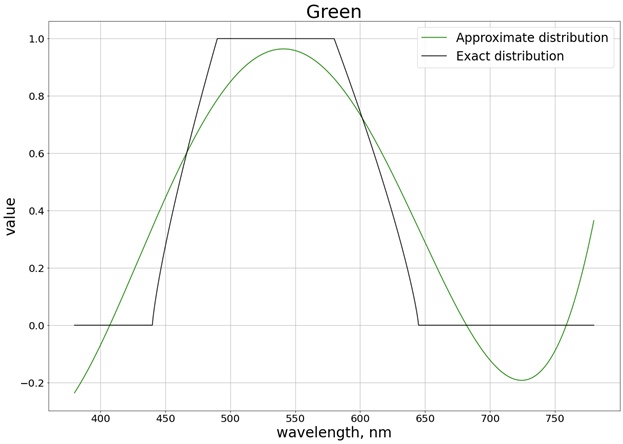
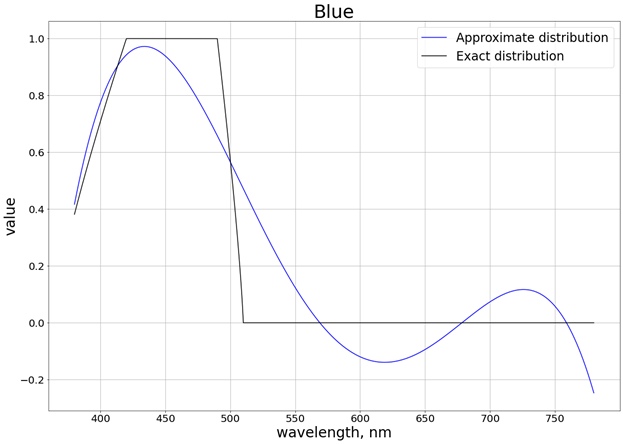
Um sicherzustellen, dass die Werte die Grenze des Segments [0, 1] nicht überschreiten, verwenden wir die Funktion saturate. Für Rot wird zum Beispiel die Funktion erhalten:

half GetRedWeight(half x)
{
    return saturate(0.8004883122689207 + 
    1.3673160565954385 * (-2.9000047500568042 + 0.005000012500149485 * x) - 
    1.244631137356407 * pow(-2.9000047500568042 + 0.005000012500149485 * x, 2) - 1.6053230172845554 * pow(-2.9000047500568042 + 0.005000012500149485*x, 3)+ 1.055933936470091 * pow(-2.9000047500568042 + 0.005000012500149485*x, 4));
}

Die fehlenden Parameter startWaveLengthund endWaveLengthin diesem Fall 780 nm bzw. 380 nm. Das Ergebnis in der Praxis sampleCount=3ist das folgende (siehe Bildränder):





Wenn wir die Werte optimieren, sampleCountauf 400 erhöhen , wird alles besser:





Leider haben wir ein Echtzeit-Rendering, bei dem wir nicht 400 Samples (ca. 3-4) in einem Shader zulassen können. Daher haben wir den Wellenlängenbereich leicht reduziert.

Teil des sichtbaren Spektrums

Nehmen wir einen Bereich, damit wir sowohl reine rote als auch reine blaue Farben erhalten. Wir lehnen auch den roten Schwanz links ab, da er das endgültige Polynom stark beeinflusst. Als Ergebnis erhalten wir die Verteilung auf das Segment [440, 670]:





Es ist auch nicht erforderlich, über das gesamte Segment zu interpolieren, da wir jetzt ein Polynom nur für das Segment erhalten können, in dem sich der Wert ändert. Für die rote Farbe ist dies beispielsweise das Segment [510, 580], in dem der Gewichtswert von 0 bis 1 variiert. In diesem Fall erhalten Sie ein Polynom zweiter Ordnung, das dann saturateauch durch die Funktion auf den Wertebereich [0, 1] reduziert wird. Für alle drei Farben erhalten wir unter Berücksichtigung der Sättigung folgendes Ergebnis:





Als Ergebnis erhalten wir zum Beispiel das folgende Polynom für Rot:

half GetRedWeight(half x)
{
    return saturate(0.5764348105166407 + 
    0.4761860550080825 * (-15.571636738012254 + 0.0285718367412005 * x) - 
    0.06265740390367036 * pow(-15.571636738012254 + 0.0285718367412005 * x, 2));
}

Und in der Praxis mit sampleCount=3:





In diesem Fall wird mit den verdrillten Einstellungen ungefähr das gleiche Ergebnis erzielt wie bei der Abtastung über den gesamten Bereich des sichtbaren Spektrums:





Mit Polynomen zweiten Grades haben wir also ein gutes Ergebnis im Wellenlängenbereich von 440 nm bis 670 nm erzielt.

Optimierung

Zusätzlich zur Optimierung der Berechnungen mit Polynomen können Sie die Arbeit des Shaders optimieren, indem Sie sich auf den Mechanismus stützen, den wir auf der Grundlage unserer lateralen chromatischen Aberration festgelegt haben, nämlich keine Berechnungen in dem Bereich durchführen, in dem die Gesamtverschiebung nicht über das aktuelle Pixel hinausgeht, andernfalls werden wir dasselbe abtasten Pixel, und wir bekommen es.



Es sieht aus wie das:

bool isNotAberrated = abs(offsetDecrement.x * g_VS_ScreenSize.x) < 1.0 && abs(offsetDecrement.y * g_VS_ScreenSize.y) < 1.0;
if (isNotAberrated)
{
    OUT.Color.rgb = tex2Dlod(baseMap, half4(IN.baseTC, 0, 0)).rgb;
    return OUT;
}

Die Optimierung ist klein, aber sehr stolz.

Fazit

Die laterale chromatische Aberration selbst sieht sehr cool aus, dieser Defekt beeinträchtigt das Visier in der Mitte nicht. Die Idee, Licht in Gewichte zu zerlegen, ist ein sehr interessantes Experiment, das ein völlig anderes Bild ergeben kann, wenn Ihre Engine oder Ihr Spiel mehr als drei Proben zulässt. In unserem Fall war es möglich, sich nicht die Mühe zu machen und einen anderen Algorithmus zu entwickeln, da wir uns selbst bei Optimierungen nicht viele Stichproben leisten können und beispielsweise der Unterschied zwischen 3 und 5 Stichproben nicht sehr sichtbar ist. Sie können selbst mit der beschriebenen Methode experimentieren und die Ergebnisse anzeigen.