
Quelle: unsplash.com
Laut Jackie Stewart, dreimaliger Formel-1-Weltmeister, hat ihm das Verständnis des Autos geholfen, ein besserer Fahrer zu werden: "Ein Rennfahrer muss kein Ingenieur sein, sondern ein Interesse an Mechanik ."
Martin Thompson ( Erfinder von LMAX Disruptor ) hat dieses Konzept auf die Programmierung angewendet. Kurz gesagt, das Verständnis der zugrunde liegenden Hardware verbessert Ihre Fähigkeiten beim Entwerfen von Algorithmen, Datenstrukturen usw.
Das Team von Mail.ru Cloud Solutions übersetzte einen Artikel , der sich eingehender mit dem Prozessordesign befasste, und untersuchte, wie Sie durch das Verständnis einiger CPU-Konzepte bessere Entscheidungen treffen können.
Die Grundlagen
Moderne Prozessoren basieren auf dem Konzept der symmetrischen Mehrfachverarbeitung (SMP). Ein Prozessor ist so konzipiert, dass sich zwei oder mehr Kerne einen gemeinsamen Speicher teilen (auch als Hauptspeicher oder Direktzugriffsspeicher bezeichnet).
Um den Speicherzugriff zu beschleunigen, verfügt der Prozessor außerdem über mehrere Cache-Ebenen: L1, L2 und L3. Die genaue Architektur hängt vom Hersteller, dem CPU-Modell und anderen Faktoren ab. Am häufigsten arbeiten L1- und L2-Caches jedoch lokal für jeden Kern, während L3 von allen Kernen gemeinsam genutzt wird.

SMP-Architektur
Je näher der Cache am Prozessorkern liegt, desto geringer sind die Zugriffslatenz und die Cache-Größe:
| Zwischenspeicher | Verzögern | CPU-Zyklen | Die Größe |
| L1 | ~ 1,2 ns | ~ 4 | Zwischen 32 und 512 KB |
| L2 | ~ 3 ns | ~ 10 | Zwischen 128 KB und 24 MB |
| L3 | ~ 12 ns | ~ 40 | Zwischen 2 und 32 MB |
Auch hier hängen die genauen Zahlen vom Prozessormodell ab. Für eine grobe Schätzung ist der Zugriff auf L1 etwa 50-mal schneller, wenn der Zugriff auf den Hauptspeicher 60 ns dauert.
In der Prozessorwelt gibt es ein wichtiges Konzept der Verbindungslokalität . Wenn der Prozessor auf einen bestimmten Speicherort zugreift, ist es sehr wahrscheinlich, dass:
- Es wird sich in naher Zukunft auf denselben Speicherort beziehen - dies ist das Prinzip der Zeitlokalität .
- Er wird sich auf Speicherzellen in der Nähe beziehen - dies ist das Prinzip der Lokalität nach Entfernung .
Die Zeitlokalität ist einer der Gründe für CPU-Caches. Aber wie nutzt man die Entfernungslokalität? Lösung - Anstatt eine Speicherzelle in die CPU-Caches zu kopieren, wird die Cache-Zeile dort kopiert. Eine Cache-Zeile ist ein zusammenhängendes Speichersegment.
Die Größe der Cache-Zeile hängt von der Cache-Ebene (und wiederum vom Prozessormodell) ab. Hier ist zum Beispiel die Größe der L1-Cache-Zeile auf meinem Computer:
$ sysctl -a | grep cacheline
hw.cachelinesize: 64
Anstatt eine einzelne Variable in den L1-Cache zu kopieren, kopiert der Prozessor dort ein zusammenhängendes 64-Byte-Segment. Anstatt beispielsweise ein einzelnes int64-Element eines Go-Slice zu kopieren, wird dieses Element plus sieben weitere int64-Elemente kopiert.
Spezifische Verwendungen für Cache-Zeilen in Go
Schauen wir uns ein konkretes Beispiel an, das die Vorteile von Prozessor-Caches demonstriert. Im folgenden Code fügen wir zwei quadratische Matrizen von int64-Elementen hinzu:
func BenchmarkMatrixCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[i][j]
}
}
}
}
Wenn
matrixLengthgleich 64k, wird das folgende Ergebnis erzeugt:
BenchmarkMatrixSimpleCombination-64000 8 130724158 ns/op
Jetzt
matrixB[i][j]fügen wir stattdessen hinzu matrixB[j][i]:
func BenchmarkMatrixReversedCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[j][i]
}
}
}
}
Wird dies die Ergebnisse beeinflussen?
BenchmarkMatrixCombination-64000 8 130724158 ns/op
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
Ja, und das ganz radikal! Wie kann man das erklären?
Versuchen wir zu zeichnen, was passiert. Der blaue Kreis zeigt die erste Matrix an und der rosa Kreis zeigt die zweite an. Wenn wir einstellen
matrixA[i][j] = matrixA[i][j] + matrixB[j][i], befindet sich der blaue Zeiger an Position (4.0) und der rosa Zeiger an Position (0.4):
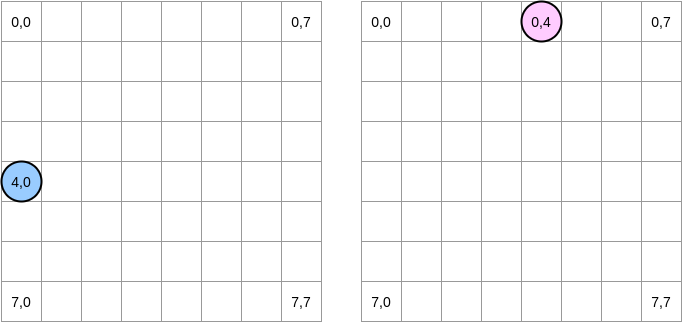
Hinweis . In diesem Diagramm werden Matrizen in mathematischer Form dargestellt: mit einer Abszisse und einer Ordinate, und die Position (0,0) befindet sich im oberen linken Quadrat. Im Speicher sind alle Zeilen der Matrix nacheinander angeordnet. Schauen wir uns jedoch der Klarheit halber die mathematische Darstellung an. Darüber hinaus ist in den folgenden Beispielen die Matrixgröße ein Vielfaches der Cache-Zeilengröße. Daher wird die Cache-Zeile in der nächsten Zeile nicht "aufholen". Es klingt kompliziert, aber die Beispiele werden alles klar machen.
Wie werden wir über Matrizen iterieren? Der blaue Zeiger bewegt sich nach rechts, bis er die letzte Spalte erreicht, und bewegt sich dann zur nächsten Zeile an Position (5,0) usw. Umgekehrt bewegt sich der rosa Zeiger nach unten und dann zur nächsten Spalte.
Wenn der rosa Zeiger die Position (0,4) erreicht, speichert der Prozessor die gesamte Zeile zwischen (in unserem Beispiel beträgt die Größe der Cache-Zeile vier Elemente). Wenn der rosa Zeiger die Position (0,5) erreicht, können wir davon ausgehen, dass die Variable bereits in L1 vorhanden ist, oder?
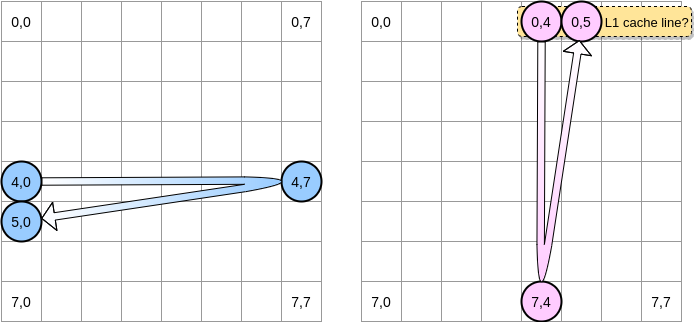
Die Antwort hängt von der Größe der Matrix ab :
- Wenn die Matrix im Vergleich zur Größe von L1 klein genug ist, wird das Element (0,5) bereits zwischengespeichert.
- Andernfalls wird die Cache-Zeile von L1 entfernt, bevor der Zeiger die Position (0,5) erreicht. Daher wird ein Cache-Fehler generiert und der Prozessor muss auf andere Weise auf die Variable zugreifen, beispielsweise über L2. Wir werden in diesem Zustand sein:
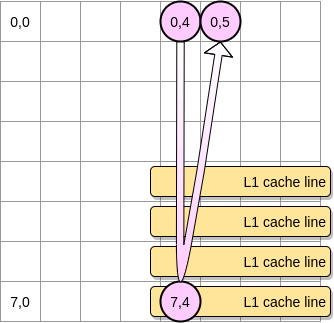
Wie klein muss eine Matrix sein, um von L1 zu profitieren? Zählen wir ein wenig. Zunächst müssen Sie die Größe des L1-Cache kennen:
$ sysctl hw.l1dcachesize
hw.l1icachesize: 32768
Auf meinem Computer beträgt der L1-Cache 32.768 Byte, während die L1-Cache-Zeile 64 Byte umfasst. Auf diese Weise kann ich bis zu 512 Cache-Zeilen in L1 speichern. Was ist, wenn wir denselben Benchmark mit einer 512-Elementmatrix ausführen?
BenchmarkMatrixCombination-512 1404 718594 ns/op
BenchmarkMatrixReversedCombination-512 1363 850141 ns/opp
Obwohl wir die Lücke behoben haben (auf einer 64k-Matrix betrug der Unterschied ungefähr das Vierfache), können wir immer noch einen leichten Unterschied feststellen. Was könnte falsch sein? In Benchmarks arbeiten wir mit zwei Matrizen. Daher muss der Prozessor die Cache-Zeilen von beiden behalten. In einer idealen Welt (keine anderen Anwendungen werden ausgeführt) ist der L1-Cache zu 50% mit Daten aus der ersten Matrix und zu 50% aus der zweiten Matrix gefüllt. Was wäre, wenn wir die Größe der Matrix um die Hälfte reduzieren würden, um mit 256 Elementen zu arbeiten:
BenchmarkMatrixCombination-256 5712 176415 ns/op
BenchmarkMatrixReversedCombination-256 6470 164720 ns/op
Schließlich haben wir den Punkt erreicht, an dem die beiden Ergebnisse (fast) gleichwertig sind.
. ? , Go. - LEA (Load Effective Address). , . LEA .
, int64 , LEA , 8 . , . , . , () .
Nun - wie kann man die Auswirkung von Cache-Fehlern bei einer größeren Matrix begrenzen? Es gibt eine Methode, die als Optimierung verschachtelter Schleifen (Loop Nest Optimization) bezeichnet wird. Um die Cache-Zeilen optimal zu nutzen, sollten wir nur innerhalb eines bestimmten Blocks iterieren.
Definieren wir in unserem Beispiel einen Block als Quadrat aus 4 Elementen. In der ersten Matrix iterieren wir von (4.0) bis (4.3). Fahren Sie dann mit der nächsten Zeile fort. Dementsprechend durchlaufen wir die zweite Matrix nur von (0.4) bis (3.4), bevor wir zur nächsten Spalte übergehen.
Wenn der rosa Zeiger über die erste Spalte fährt, speichert der Prozessor die entsprechende Cache-Zeile. Wenn Sie also den Rest des Blocks durchgehen, müssen Sie L1 ausnutzen:
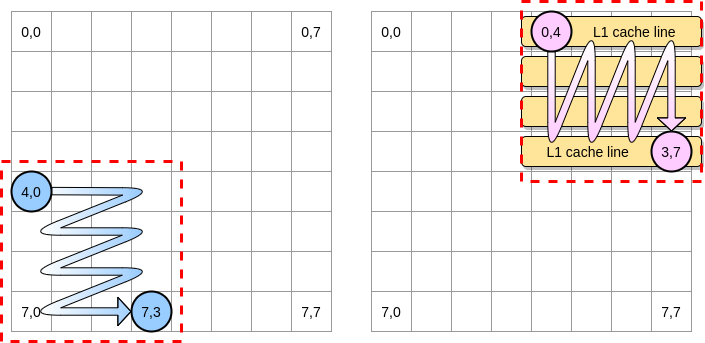
Lassen Sie uns eine Implementierung dieses Algorithmus in Go schreiben, aber zuerst müssen wir die Blockgröße sorgfältig auswählen. Im vorherigen Beispiel war es gleich der Cache-Zeile. Es darf nicht kleiner sein, sonst speichern wir Elemente, auf die nicht zugegriffen werden kann.
In unserem Go-Benchmark speichern wir int64-Elemente (jeweils 8 Byte). Die Cache-Zeile ist 64 Byte groß und kann daher 8 Elemente enthalten. Dann muss der Blockgrößenwert mindestens 8 betragen:
func BenchmarkMatrixReversedCombinationPerBlock(b *testing.B){
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
blockSize := 8
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i += blockSize {
for j := 0; j < matrixLength; j += blockSize {
for ii := i; ii < i+blockSize; ii++ {
for jj := j; jj < j+blockSize; jj++ {
matrixA[ii][jj] = matrixA[ii][jj] + matrixB[jj][ii]
}
}
}
}
}
}
Unsere Implementierung ist jetzt über 67% schneller als bei der Iteration über die gesamte Zeile / Spalte:
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
BenchmarkMatrixReversedCombinationPerBlock-64000 6 185375690 ns/op
Dies war das erste Beispiel, das demonstrierte, dass das Verständnis der Funktionsweise von CPU-Caches dazu beitragen kann, effizientere Algorithmen zu entwerfen.
Falsches Teilen
Wir verstehen jetzt, wie der Prozessor interne Caches verwaltet. Als kurze Zusammenfassung:
- Das Prinzip der Lokalität nach Entfernung zwingt den Prozessor, nicht nur eine Speicheradresse, sondern eine Cache-Zeile zu verwenden.
- Der L1-Cache befindet sich lokal in einem Prozessorkern.
Lassen Sie uns nun ein Beispiel mit L1-Cache-Kohärenz diskutieren. Der Hauptspeicher speichert zwei Variablen
var1und var2. Ein Thread auf einem Kern greift zu var1, während ein anderer Thread auf dem anderen Kern zugreift var2. Angenommen, beide Variablen sind kontinuierlich (oder nahezu kontinuierlich), geraten wir in eine Situation, in der sie var2in beiden Caches vorhanden sind.
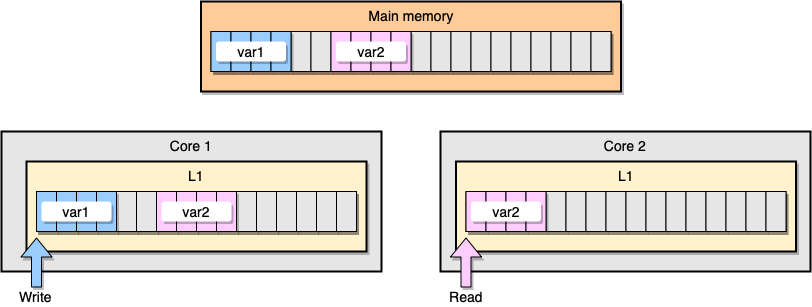
Beispiel L1-Cache
Was passiert, wenn der erste Thread seine Cache-Zeile aktualisiert? Es kann möglicherweise jeden Speicherort seiner Zeichenfolge aktualisieren, einschließlich
var2. Wenn dann der zweite Thread liest var2, ist der Wert möglicherweise nicht konsistent.
Wie hält der Prozessor den Cache kohärent? Wenn zwei Cache-Zeilen gemeinsam genutzte Adressen haben, markiert der Prozessor diese als gemeinsam genutzt. Wenn ein Thread eine gemeinsam genutzte Zeile ändert, werden beide als geändert markiert. Die Koordination zwischen den Kernen ist erforderlich, um die Kohärenz der Caches sicherzustellen, was die Anwendungsleistung erheblich beeinträchtigen kann. Dieses Problem wird als falsches Teilen bezeichnet .
Betrachten wir eine bestimmte Go-Anwendung. In diesem Beispiel erstellen wir zwei Strukturen nacheinander. Daher müssen diese Strukturen im Speicher sequentiell sein. Dann erstellen wir zwei Goroutinen, von denen sich jede auf ihre eigene Struktur bezieht (M ist eine Konstante gleich einer Million):
type SimpleStruct struct {
n int
}
func BenchmarkStructureFalseSharing(b *testing.B) {
structA := SimpleStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
In diesem Beispiel steht die Variable n der zweiten Struktur nur der zweiten Goroutine zur Verfügung. Da die Strukturen im Speicher zusammenhängend sind, ist die Variable in beiden Cache-Zeilen vorhanden (vorausgesetzt, beide Goroutinen sind auf Threads auf separaten Kernen geplant, was nicht unbedingt der Fall ist). Hier ist das Benchmark-Ergebnis:
BenchmarkStructureFalseSharing 514 2641990 ns/op
Wie kann ein falscher Informationsaustausch verhindert werden? Eine Lösung ist der vollständige Speicher (Speicherauffüllung). Unser Ziel ist es, sicherzustellen, dass zwischen zwei Variablen genügend Platz ist, damit sie zu verschiedenen Cache-Zeilen gehören.
Erstellen wir zunächst eine Alternative zur vorherigen Struktur, indem wir den Speicher nach dem Deklarieren der Variablen füllen:
type PaddedStruct struct {
n int
_ CacheLinePad
}
type CacheLinePad struct {
_ [CacheLinePadSize]byte
}
const CacheLinePadSize = 64
Dann instanziieren wir die beiden Strukturen und greifen weiterhin auf diese beiden Variablen in separaten Goroutinen zu:
func BenchmarkStructurePadding(b *testing.B) {
structA := PaddedStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
Aus Speichersicht sollte dieses Beispiel so aussehen, als ob die beiden Variablen Teil verschiedener Cache-Zeilen sind:
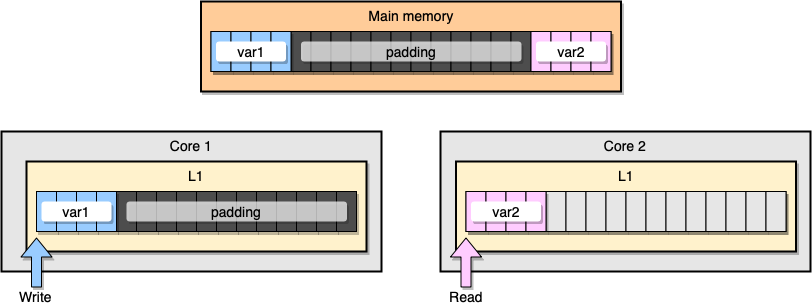
Speicherfüllung
Schauen wir uns die Ergebnisse an:
BenchmarkStructureFalseSharing 514 2641990 ns/op
BenchmarkStructurePadding 735 1622886 ns/op
Ein zweites Beispiel mit Speicherfüllung ist etwa 40% schneller als unsere ursprüngliche Implementierung. Es gibt aber auch einen Nachteil. Die Methode beschleunigt den Code, benötigt jedoch mehr Speicher.
Die Mechanik zu mögen ist ein wichtiges Konzept, wenn es darum geht, Apps zu optimieren. In diesem Artikel haben wir Beispiele dafür gesehen, wie das Verständnis der CPU uns geholfen hat, die Programmgeschwindigkeit zu verbessern.
Was noch zu lesen: