
Vielen Dank. Ich entschuldige mich dafür, dass ich hier sitze. Ich bin ein sehr alter Mann.
Mein heutiges Thema ist in gewisser Hinsicht etwas ganz Besonderes, weil es sehr alt ist. Knicke sind ein wesentlicher Bestandteil des menschlichen Lebens, sie sind immer da. Die Alten haben darüber geschrieben. Diese Sache ist weitgehend außerhalb unserer Kontrolle. Und in gewissem Sinne scheinen sie ein extremer Grad an Komplikation zu sein - nur ein komplettes Durcheinander.
Es gibt viele Arten von Störungen. Zufällig begann ich mich vor vielen Jahren mit dieser Form der Komplikation zu befassen, und zu meiner großen Überraschung fand ich Anzeichen und, ich muss sagen, sehr deutliche Anzeichen für Ordnung in den Knicken. Deshalb möchte ich Ihnen heute einige Beispiele dafür vorstellen, was dies bedeutet. Ich bevorzuge das Wort „gebrochen“ gegenüber „ungleichmäßig“, weil für jemanden, der Latein gelernt hat, wie ich in meiner fernen Jugend, Ungleichmäßigkeit das Gegenteil von Gleichmäßigkeit ist. Dies ist jedoch nicht der Fall.
Gleichheit ist das Gegenteil von Bruch, weil uns die Welt größtenteils als voller Brüche erscheint.
Lassen Sie mich Ihnen einige Objekte zeigen. Einige von ihnen sind künstlich geschaffen. Andere sind in gewissem Sinne sehr real. Das ist die wahre Sache.

Das ist Blumenkohl. Warum zeige ich Ihnen Blumenkohl, eine gewöhnliche und alte Pflanze? Weil es trotz seiner Routine und Antike komplex und einfach ist. es ist komplex und einfach. Zum Beispiel ist es nicht schwierig, es zu wiegen. Gewicht ist wichtig, wenn wir es essen wollen. Aber nehmen wir an, wir werden seine Oberfläche messen. Das wird interessant. Nachdem wir eine der Blumenkohlblüten mit einem scharfen Messer ausgeschnitten haben und genau hinschauen, sehen wir den ganzen Blumenkohl, nur von kleinerer Größe. Dann können Sie immer wieder und immer wieder und immer wieder schneiden ... Und Sie bekommen immer kleinere Exemplare von Blumenkohl. Die menschliche Erfahrung hat gezeigt, dass es Formen mit einer so interessanten Eigenschaft gibt, dass jeder Teil dem Ganzen ähnlich ist, aber eine kleinere Größe hat. Und was hat die Person daraus gelernt? Sehr wenig.
Im Zusammenhang mit der Untersuchung dieses Problems entdeckte ich etwas völlig Erstaunliches: Knick kann an einer Zahl gemessen werden, beispielsweise 2,3 oder 1,2, und manchmal auch an vielem mehr. Eines Tages brachte ein Freund von mir ein Foto und fragte halb im Scherz: "Was ist der Knick dieser Kurve?" Ich sagte: "Etwas weniger als eineinhalb." Wie sich herausstellte, war es gleich 1,48. Es dauerte nicht lange, bis ich diese Dinge so lange studiert hatte. Die fraglichen Zahlen geben den Bruchgrad der Oberfläche an.

Lassen Sie mich gleich reservieren, dass die Oberflächen absolut künstlich sind und auf einem Computer erstellt wurden. Der einzige Ausgangspunkt war die Nummer. Diese Nummer ist Knick. Der Bruch links ist das Ergebnis des Kopierens aus mehreren Landschaften. Rechts - ich habe selbst einen höheren Knick gesetzt. Wenn Sie genau hinschauen, können Sie nach einer Weile die Unterschiede in diesen beiden Fällen mit bloßem Auge erkennen.
Der Mensch musste sich an das Konzept der Fraktur gewöhnen. Das ist sehr kaputt, aber das könnte man sagen, ist glatt, aber das ist völlig glatt. Nur wenige Dinge sind sehr glatt. Stellen wir uns nun die Frage: Was ist die Oberfläche des Blumenkohls? Es kann gemessen und gemessen und gemessen werden ... Je genauer die Messung, desto größer die Oberfläche usw. bis auf sehr kleine Entfernungen. Wie lang ist die Küste dieser Seen? Je genauer die Messung ist, desto länger wird sie ausfallen. Das Konzept der Küstenlänge, das so offensichtlich erscheint, weil es oft zitiert wird, ist in der Tat völlig falsch: Es gibt einfach keine solche. Es muss einen anderen Ansatz geben.
Und wozu dient dieses Wissen? Überraschenderweise gibt es viele Vorteile. Zunächst werden die künstlichen Landschaften, die ich erfunden habe, ständig in der Kinematographie verwendet. In der Ferne sehen wir Berge. Es können Berge sein, aber es können auch nur fließende Formeln sein. Dies ist sehr einfach zu erreichen. Früher hat es lange gedauert, aber jetzt ist es nur noch eine Kleinigkeit. Schauen Sie hier. Das ist echtes Licht.
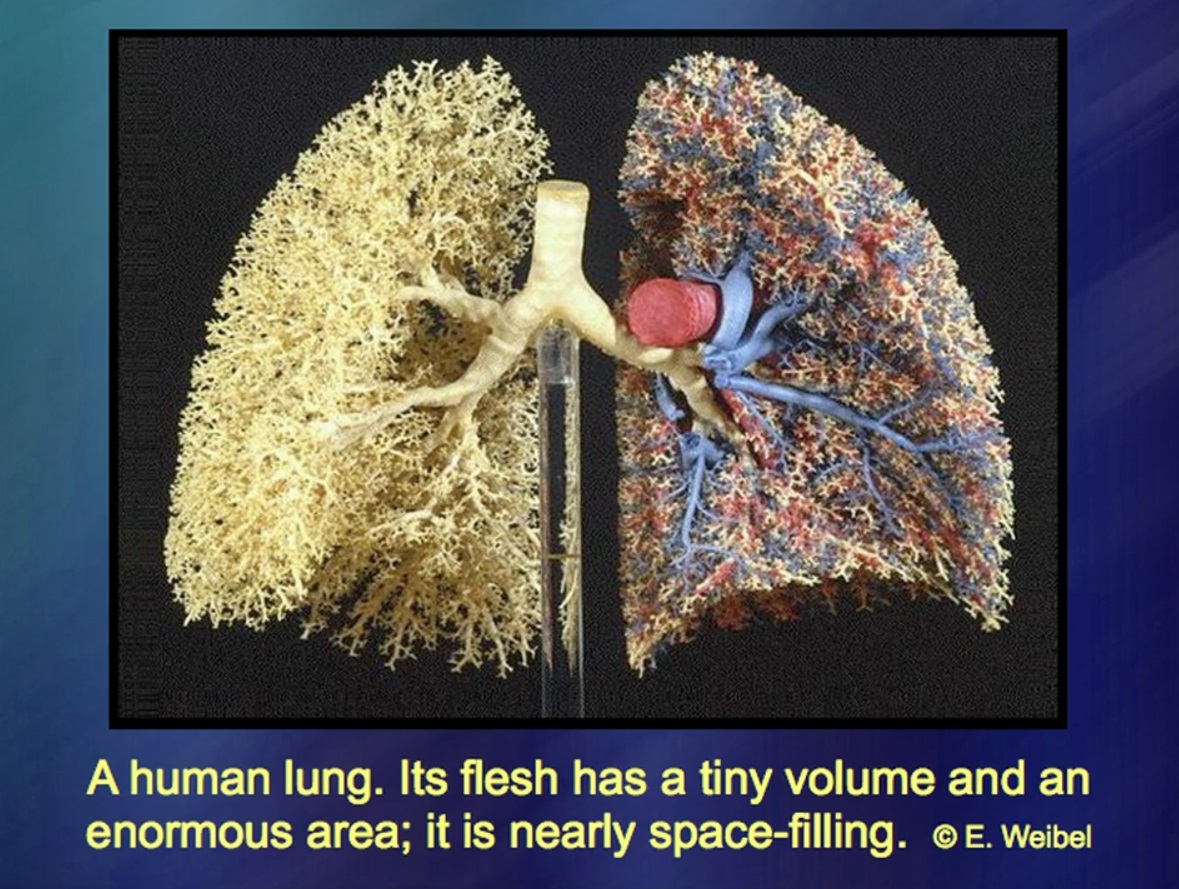
Die Lunge ist ein sehr seltsames Objekt. Wir alle wissen sehr gut, dass es etwas Gewicht hat. Es ist auch bekannt, dass das Lungenvolumen sehr klein ist. Was ist mit Lungenbereich? Anatomisten haben dieses Thema lange diskutiert. Es wird angenommen, dass bei einem normalen Mann die Fläche der Lunge gleich der Fläche eines Basketballs ist. Andere argumentieren, dass es keine fünf solchen Bälle gibt. Die Diskrepanzen sind kolossal. Warum? Weil der Bereich der Lunge ein sehr vage definiertes Konzept ist. Die Bronchien verzweigen sich und verzweigen sich tiefer und tiefer. Und sie hören nicht aufgrund eines Prinzips auf zu verzweigen, sondern aufgrund rein physischer Bedingungen, aufgrund von Schleim in der Lunge. So entsteht eine viel größere Lunge: Die Bronchien verzweigen sich immer tiefer, während der Abstand zwischen ihnen für einen Wal, eine Person und ein kleines Nagetier ungefähr gleich ist.
Was nützt das? Überraschenderweise und sogar erstaunlich, hatten Anatomen bis vor kurzem eine schlechte Vorstellung von der Struktur der Lunge. Ich denke, meine mathematische Forschung war überraschenderweise eine große Hilfe für Chirurgen, die Lungenerkrankungen sowie Lebererkrankungen untersuchen, bei denen es solche Verzweigungssysteme mit einem Mangel an verständlicher Geometrie gibt. Mit anderen Worten, ich musste Geometrie für etwas erstellen, das keine eigene Geometrie hat. Es wurde eine überraschende Qualität festgestellt: Sehr oft sind die Regeln dieser Geometrie äußerst präzise. Sie beginnen mit kurzen Formeln, wenden sie mehrmals, manchmal wiederholt, immer und immer wieder an. Die gleiche Wiederholung. Und am Ende stellt sich so etwas heraus.
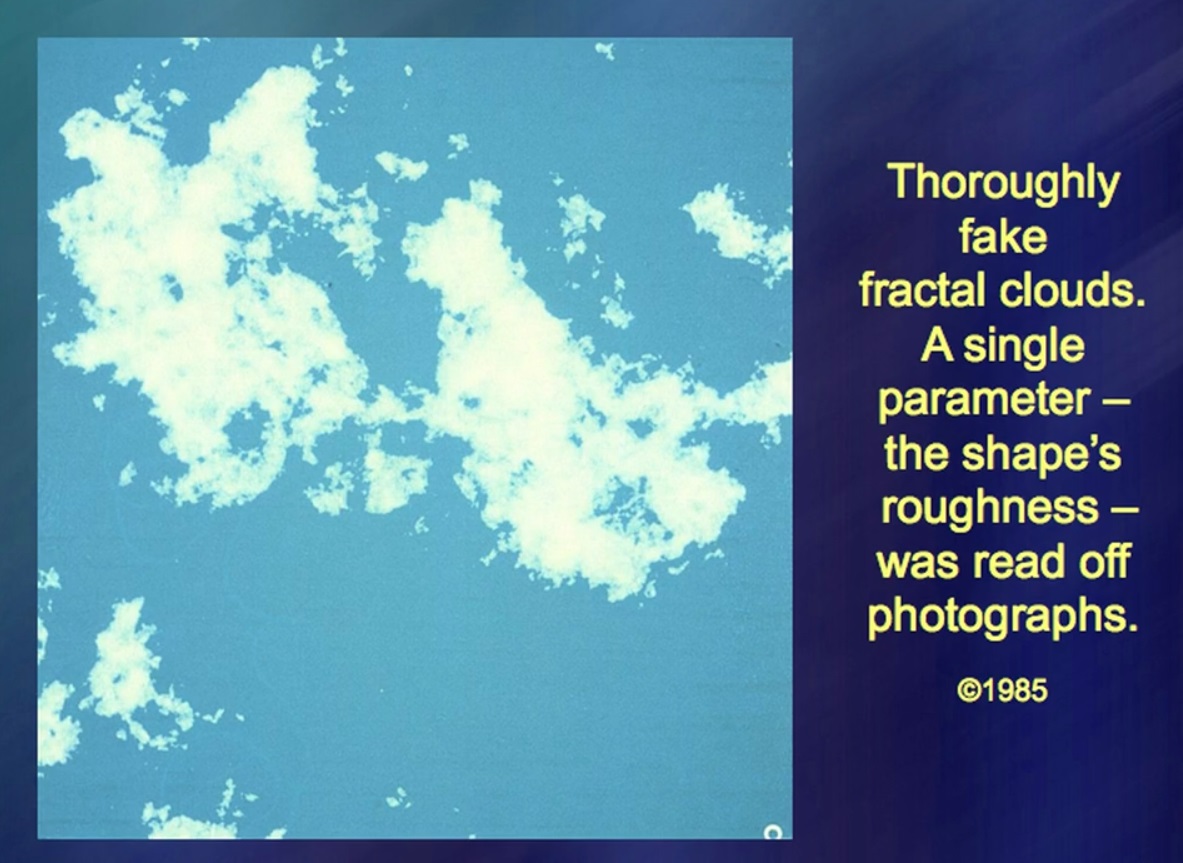
Diese Wolke ist zu 100% vollständig künstlich. Okay, 99,9%. Das einzige natürliche Element hier ist die Zahl, der Bruch der Wolke - diese Zahl stammt aus der Natur. Eine so komplexe Sache wie eine Wolke, die so instabil und veränderlich ist, folgt einer einfachen Regel. Diese einfache Regel ist keine Erklärung für die Trübung. Aber das Wolkenmeer muss diese Regel berücksichtigen. Ich weiß nicht, wie perfekt diese alten Fotos sind. Ich habe das intensiv gemacht, aber dann war meine Aufmerksamkeit auf andere Phänomene gerichtet.
Und hier ist noch eine interessante Sache. Eines der revolutionären Ereignisse in der Geschichte der Mathematik, das von vielen nicht ausreichend gewürdigt wurde, ereignete sich vor etwa 130 Jahren, vor 145 Jahren. Mathematiker begannen, nicht existierende Formen zu schaffen. Unter Mathematikern wurde die Fähigkeit eines Menschen, etwas zu erschaffen, das es in der Natur nie gab, zu einem absolut unvorstellbaren Grad geschätzt. Insbesondere konnten sie eine Kurve erfinden, die die gesamte Ebene bis zum letzten Punkt ausfüllt. Eine Kurve ist eine Kurve, eine Ebene ist eine Ebene und die beiden passen nicht zusammen. Es stellte sich heraus, dass sie zusammenpassen.
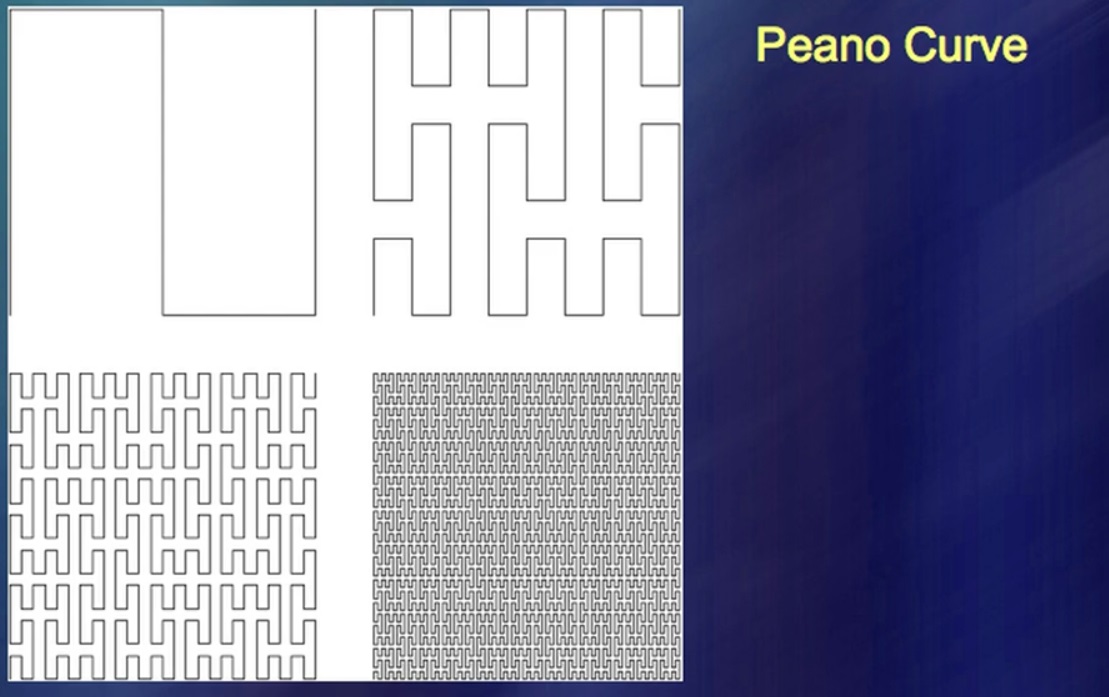
Ein Mann namens Peano identifizierte solche Kurven und sie stießen auf außergewöhnliches Interesse. Sie sind sehr wichtig und wecken größtenteils Interesse, weil es eine Art Aufteilung der Mathematik in eine gegeben hat, die auf der Realität basiert und aus reiner Vernunft stammt. Leider habe ich zufällig bewiesen, dass das, was durch die Bemühungen der reinen Vernunft bekannt wurde, tatsächlich seit langem in einer anderen Form bekannt ist. Hier habe ich ein System von Bächen in Form von Kurven, die die Ebene füllen.

An sich ist das Geschichte. Es war zwischen 1875 und 1925, eine erstaunliche Zeit, als sich die Mathematik darauf vorbereitete, sich von der realen Welt zu lösen. Bestimmte Objekte haben seit meiner Kindheit und meiner Studienzeit die Kluft zwischen Mathematik und sichtbarer Realität veranschaulicht. Es gelang mir jedoch, sie zu überdenken, auf den Kopf zu stellen und mit ihrer Hilfe einige Aspekte der Komplexität der Natur zu beschreiben.
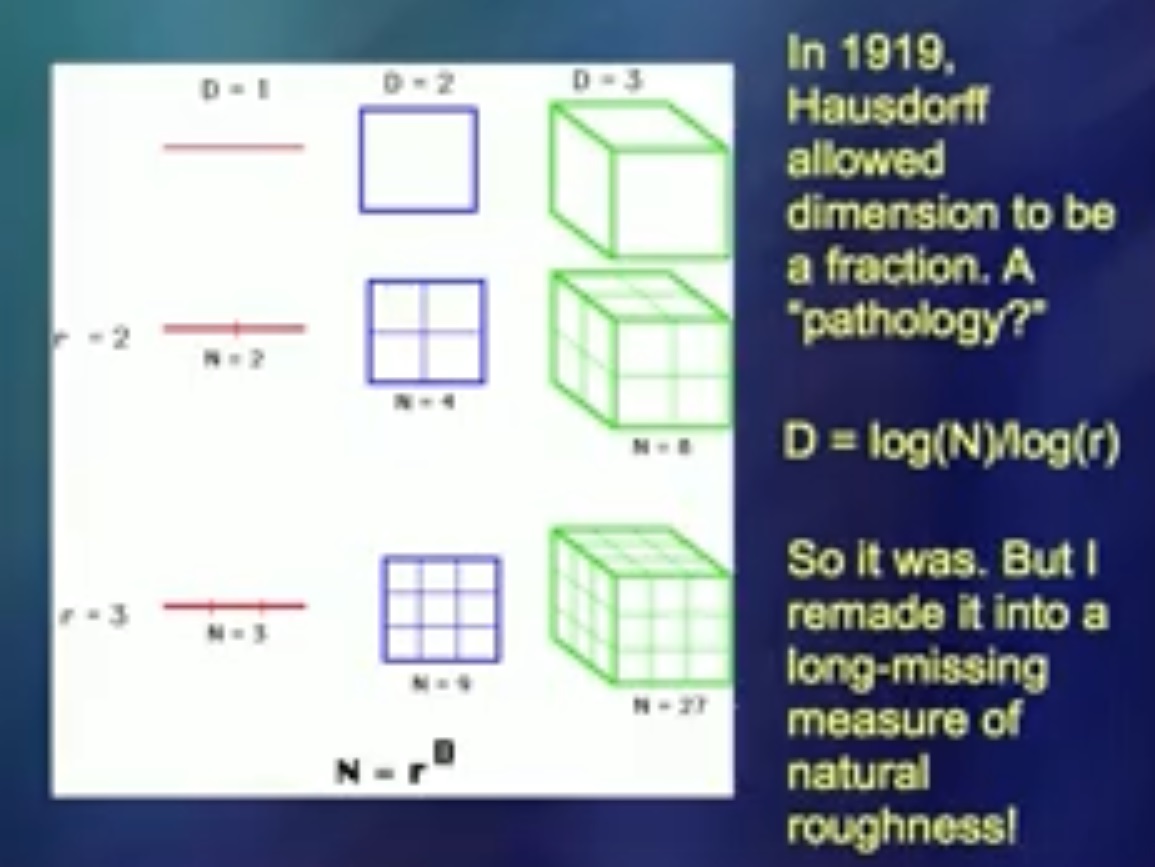
1919 identifizierte ein Mann namens Hausdorff eine Zahl, die als mathematischer Witz angesehen werden konnte. Aber ich habe festgestellt, dass diese Zahl ein gutes Werkzeug zum Messen von Knicken ist. Als ich meinen Kollegen zum ersten Mal davon erzählte, sagten sie: „Sei nicht albern. Das ist etwas ... “Eigentlich habe ich keine dummen Dinge getan.

Der große Künstler Hokusai wusste das sehr gut. Am unteren Rand des Bildes befinden sich Algen. Hokusai kannte die notwendige Mathematik nicht: Sie existierte damals einfach nicht. Als Japaner hatte er zu dieser Zeit keinen Kontakt zum Westen. Aber Kunst enthält seit langem fraktale Elemente. Ich kann lange darüber sprechen.

Der Eiffelturm hat fraktale Elemente. Ich habe Eiffels Buch über seinen Turm gelesen - der Umfang seines Verständnisses ist erstaunlich.
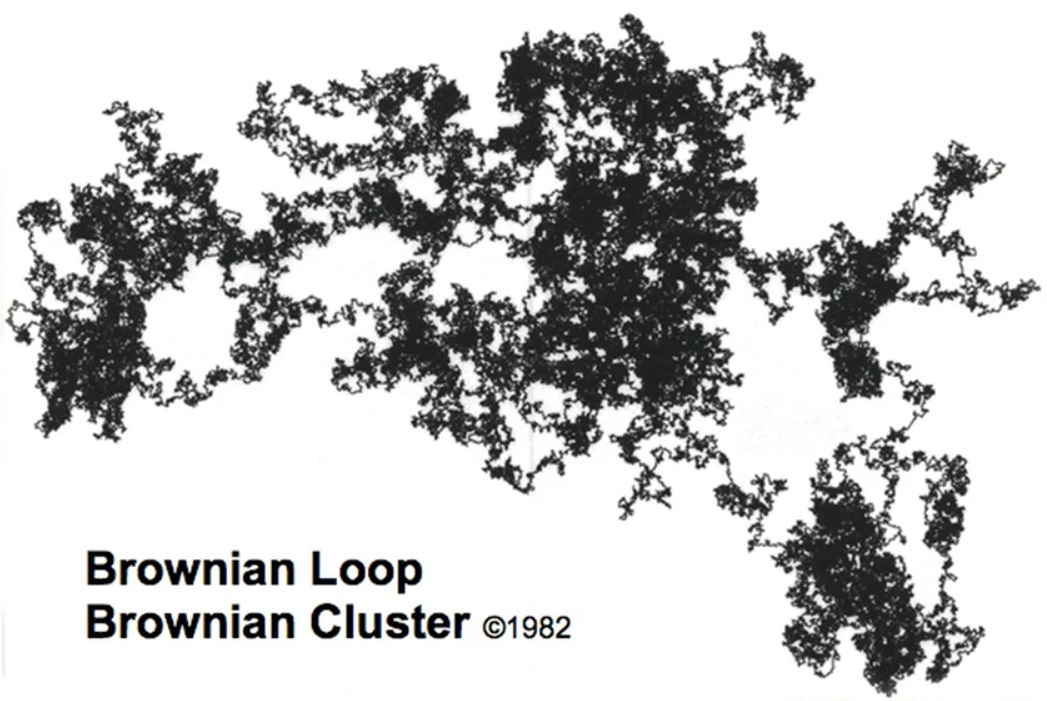
Hier ist ein Durcheinander in einem Durcheinander. Brownsche Schleife. Als ich mich entschied, dass ich einen beträchtlichen Teil meines Berufslebens durchlaufen hatte und so viele verschiedene Dinge mich beschäftigten, entschied ich, dass es Zeit war, mich selbst zu testen. Kann ich ein Objekt erkunden, das jeder schon lange erforscht hat, und darin etwas radikal Neues finden? Ich begann alles zu studieren, was in die Kategorie der Brownschen Bewegung fällt. Ich habe verschiedene Blickwinkel ausprobiert, verschiedene Methoden ausprobiert und bin dorthin zurückgekehrt, wo ich angefangen habe. Dann schlug ich meinem Assistenten vor: „Ich sehe hier nichts. Kannst du übermalen? " Er tat dies, das heißt, er füllte alle Innenseiten. "Es gelang mir…"

Aber ich rief: „Hör auf! Halt! Halt! Verstanden: Dies ist eine Insel. " Tolle. Brownsche Bewegung hat einen Knick gleich zwei. Ich messe es, es stellt sich heraus, 1,33. Ich messe immer wieder. Lange Messungen, große Brownsche Bewegungen. Nochmals: 1.33. Es entsteht sofort ein mathematisches Problem: Wie kann man es beweisen? Meine Freunde haben 20 Jahre gebraucht. Drei hatten unvollständige Beweise. Sie schlossen sich zusammen und zusammen gelang es ihnen, Beweise zu erhalten. Infolgedessen wurden sie mit der berühmten [Fields] -Medaille für Mathematiker ausgezeichnet. Insgesamt erhielten Mathematiker drei [Fields] -Medaillen für den Nachweis von Tatsachen, die ich sah, aber nicht beweisen konnte.
Jetzt fragen mich die Leute überall: „Wie hat alles angefangen? Wie hat dich dein Studium zu so ungewöhnlichen Dingen geführt? "
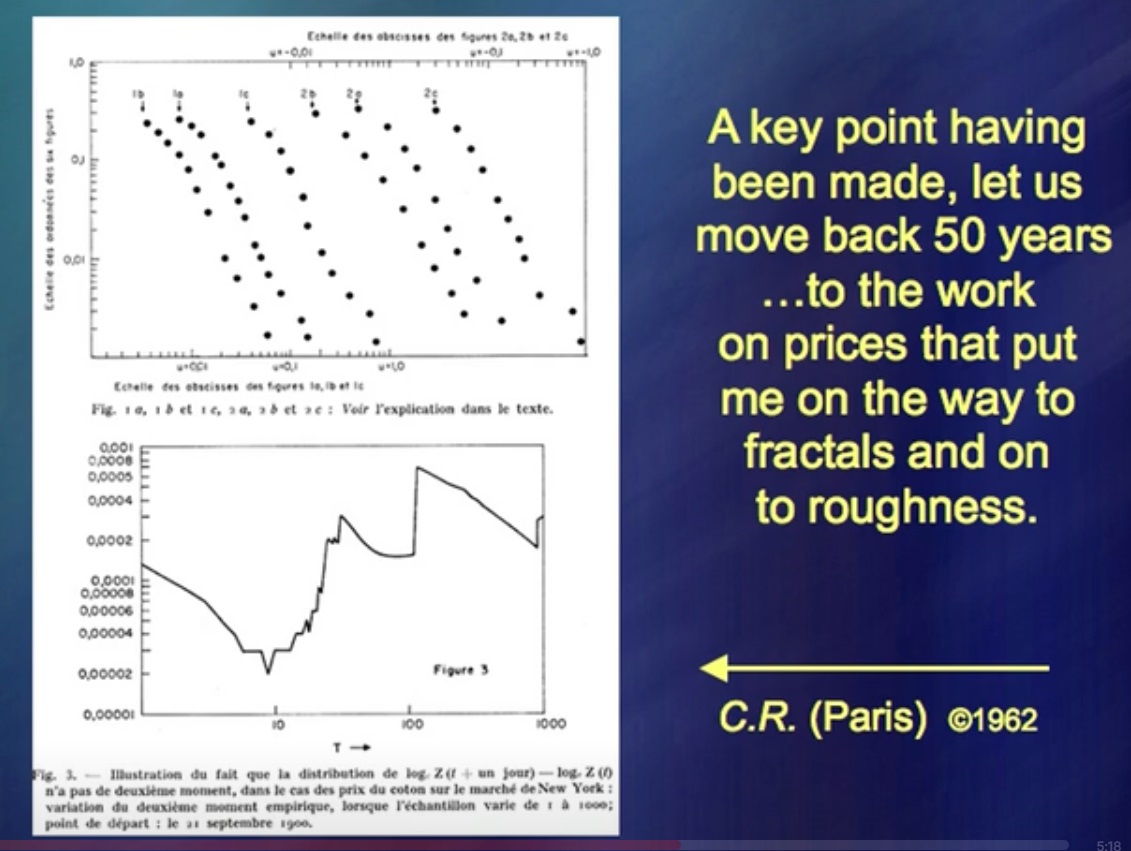
Was erlaubte mir, gleichzeitig Maschinenbauingenieur, Geograph, Mathematiker usw. zu sein? Seltsamerweise habe ich zunächst die Kurse an der Börse untersucht.

Ich hatte eine Theorie und schrieb Bücher darüber.
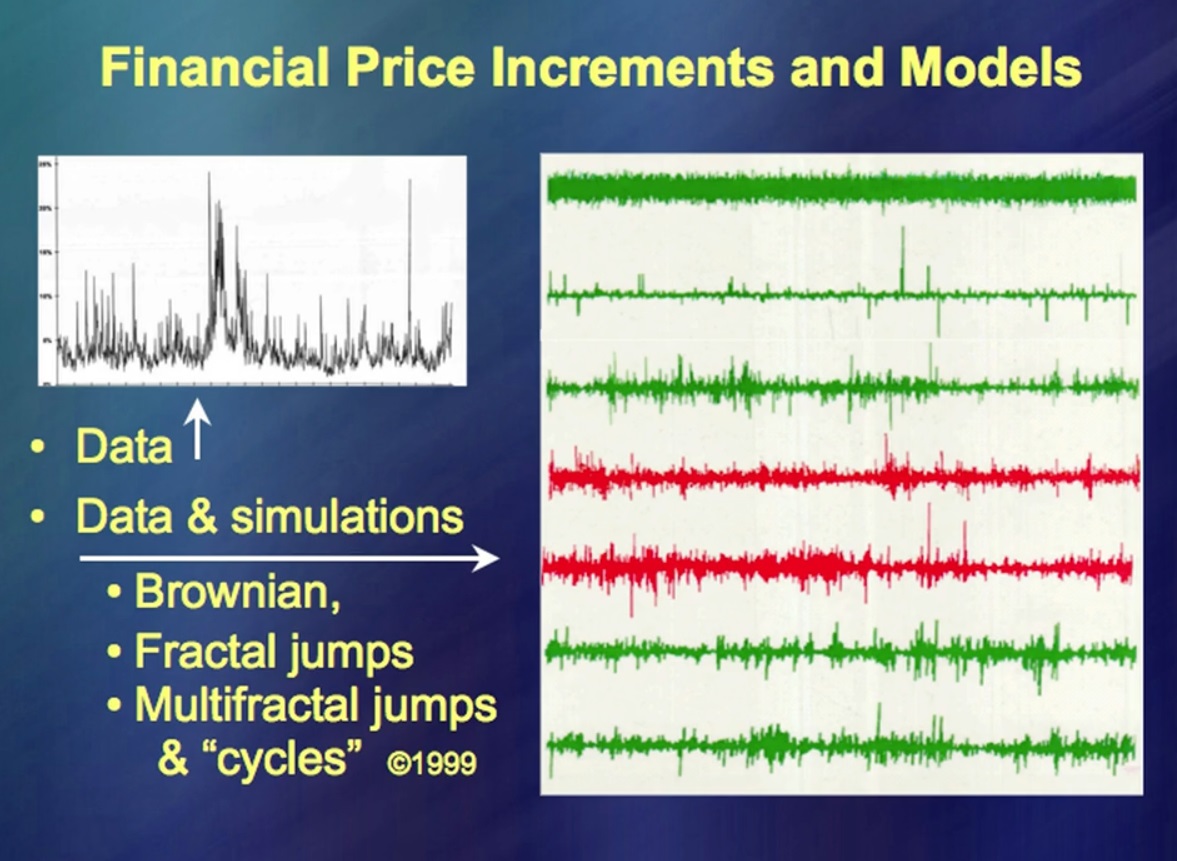
"Preisbewegungen von Finanzinstrumenten" Links sehen Sie die Daten für einen langen Zeitraum, rechts oben - die Daten nach einer sehr, sehr modischen Theorie. Es ist sehr einfach und Sie können sehr schnell viele Bücher darüber schreiben. (Gelächter) Es gibt Tausende von Büchern zu diesem Thema. Vergleichen Sie nun mit realen Preisbewegungen. Und wo sind sie? Zusätzliche Zeilen beinhalten echte Preisbewegungen sowie eine kleine Fälschung meinerseits. Die Hauptidee dort war, dass Sie in der Lage sein müssen ... Wie heißt es? … Simulation von Preisschwankungen. Das hat vor 50 Jahren großartig funktioniert.
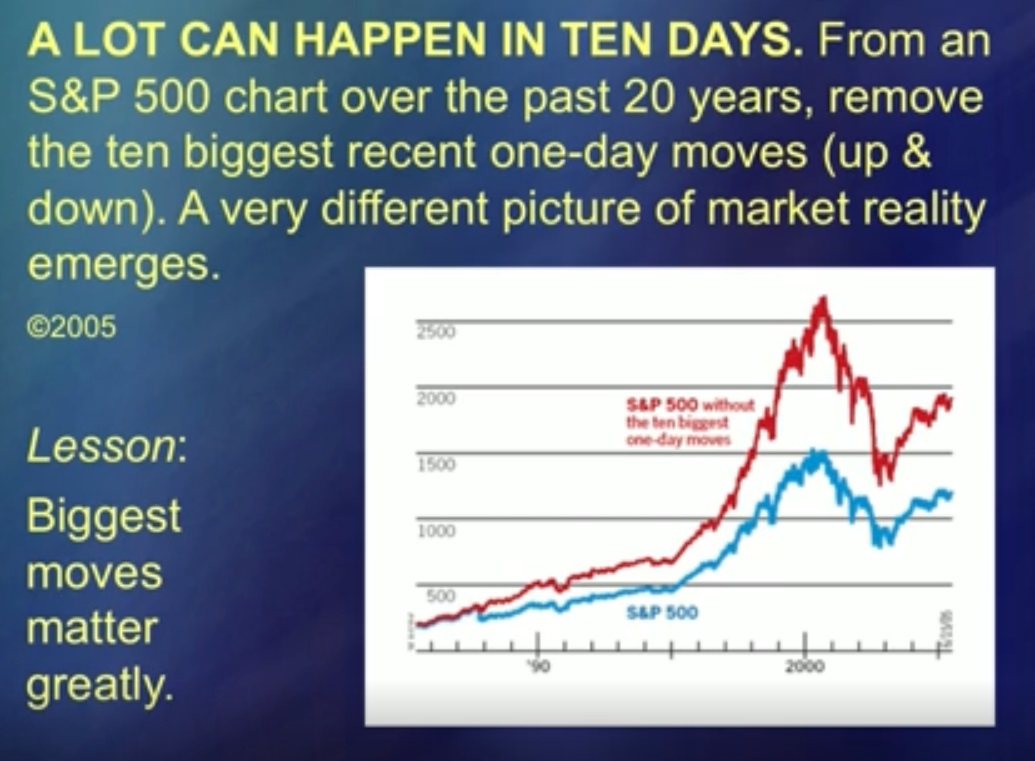
50 Jahre lang wurde meine Idee lächerlich gemacht, weil es einfacher hätte gemacht werden können. Aber jetzt, sage ich dir, fingen sie an, mir zuzuhören. (Gelächter) Diese beiden Kurven repräsentieren Durchschnittswerte. Blau ist der Standard und der Poor's [S & P 500] und Rot ist der Standard und der Poor's, von denen die 5 größten Preisspitzen abgezogen wurden. Der Sprung verdirbt sicherlich die Analyse, und in vielen Studien wird er als [nicht analytischer] Sonderfall angesehen. „Unglaublicher Zufall, Eingreifen des Herrn. Nun, ein kleines Ding, du kannst es einfach beiseite legen. " Die Eingriffe des Herrn in diese Grafik, und es gibt genau fünf davon, wie sich herausstellt, sind genauso wichtig wie alles andere. Mit anderen Worten, die Interventionen des Herrn können nicht beiseite gelegt werden.
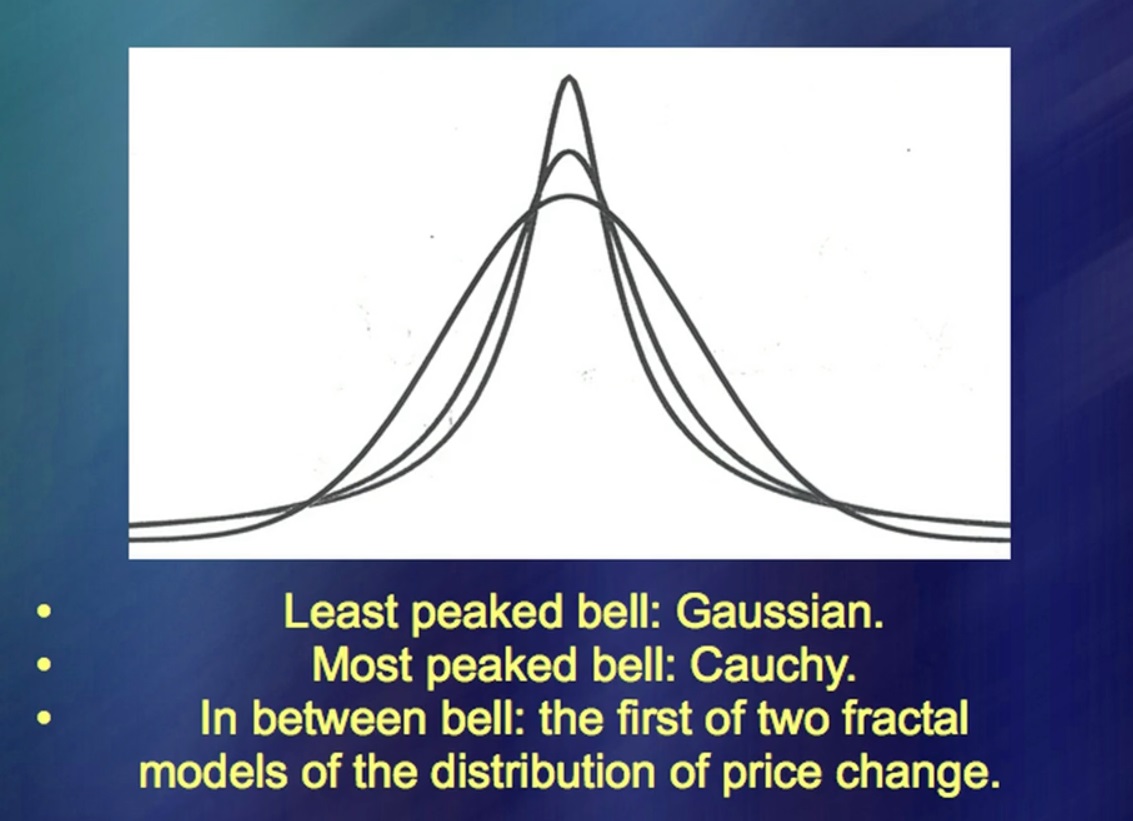
Es ist ein Wesen, es ist das eigentliche Objekt der Analyse. Wenn Sie sich mit ihnen befassen, können Sie sich auch mit Preisbewegungen befassen. Aber ich habe die Sprünge nicht herausgefunden, dann können Sie das sogenannte Rauschen so oft analysieren, wie Sie möchten, aber diese Analyse wird keinen Sinn ergeben. Diese Kurven zeigen die Auswirkungen.

Jetzt komme ich zum letzten Thema - dem nach mir benannten Set. In gewisser Weise ist dies die Geschichte meines Lebens. Meine Jugend verbrachte ich in Frankreich, das in diesen Jahren von Deutschland besetzt war. Da ich dachte, dass ich es jeden Moment nicht sein könnte, hatte ich große Träume. Nach dem Krieg traf ich meinen Onkel wieder. Mein Onkel war ein hervorragender Mathematiker und sagte: „Hier ist ein Problem für Sie. Vor 25 Jahren konnte ich es nicht lösen und niemand kann es lösen. Dies ist die Konstruktion eines Mathematikers namens Gaston Julia und eines anderen namens Pierre Fatou. Wenn Sie hier etwas Neues finden - irgendetwas - denken Sie daran, dass Ihre Karriere gesichert ist. " Sehr einfach. Ich begann dieses Problem zu untersuchen und erreichte wie Tausende von denen, die es vor mir versuchten, nichts.
Aber dann kamen Computer. Und ich entschied, dass ich Rechenleistung nicht auf neue mathematische Probleme anwenden musste - wie zum Beispiel diese geschwungene Sache: Dies ist ein neues Problem - sondern auf alte Probleme. Und ich wechselte von den sogenannten reellen Zahlen, d.h. von Punkten auf einer geraden Linie bis zu komplexen Zahlen, und dies sind Punkte auf einer Ebene, das heißt, was für dieses Problem erforderlich ist. Das Ergebnis ist eine solche Zahl.

Dieser ist von außergewöhnlicher Komplexität. Die Gleichung ist darin verborgen: z transformiert sich in z ^ 2 + c. So einfach und langweilig, so uninteressant. Lassen Sie es uns jetzt einmal, zweimal ausführen ... Zweimal ist genug. Über ein Wunder! Dies ist, was erscheint. Ich werde diese Dinge hier nicht erklären, aber es stellt sich heraus, dass dies was ist und das ist was.


Figuren von solcher Komplexität, solcher Harmonie und solcher Schönheit werden immer und immer wieder erhalten. Meine Hauptentdeckung war, dass diese Inseln mehr oder weniger die gleiche Form haben wie die ganze Figur. Das Ergebnis ist solch atemberaubender Barockschmuck.

Und all diese kurze Formel, in der es alles gibt - wie viel gibt es? - fünf Symbole. Und das ist das Ergebnis.

Die Farbe wurde aus zwei Gründen hinzugefügt. Erstens, weil die Zahlen so komplex sind, dass es schwierig ist zu erkennen, welche Bedeutung die Zahlen haben. Und Sie müssen eine Art System auswählen, um sie im Flugzeug zu reflektieren. Daher habe ich es als Prinzip genommen, die Figuren immer in verschiedenen Farben darzustellen: Eine Farbe bedeutet eine Sache und eine andere bedeutet eine andere usw. Es ist so hart.
1990 war ich in Großbritannien in Cambridge, wo ich einen Preis von der Universität erhielt. Drei Tage später sah dies ein Pilot, der über das Feld flog.

Woher würde so etwas kommen? Natürlich - von den Außerirdischen.
Eine der Zeitungen in Cambridge veröffentlichte einen Artikel über diese "Entdeckung" und erhielt am nächsten Tag fünftausend Briefe, in denen stand, dass dies das Mandelbrot-Set ist, das nur sehr groß ist.

Lass mich fertig machen. Dieses Bild wird durch reine Mathematik erhalten. Einfache Regeln können ein Wunder ohne Boden schaffen, wenn sie endlos wiederholt werden.
Übersetzt von Namik Kasumov
Bewertet von Ekaterina Tsvetkova

Erfahren Sie, wie Sie einen begehrten Beruf von Grund auf neu erlernen oder Ihre Fähigkeiten und Ihr Gehalt verbessern können, indem Sie bezahlte Online-Kurse von SkillFactory absolvieren:
- Machine Learning (12 )
- Data Science (12 )
- (9 )
- «Python -» (9 )
- Data Sciene 2020
- Data Science . Business Science
- Data Scientist
- Data Scientist -
- Data Science
- Data Science : «data»
- Data Sciene : Decision Intelligence