9 wichtige Algorithmen für maschinelles Lernen im Klartext

Hallo Habr! Ich präsentiere Ihnen die Übersetzung des Artikels "9 wichtige Algorithmen für maschinelles Lernen, erklärt in einfachem Englisch" von Nick McCullum .



Maschinelles Lernen (ML) verändert bereits die Welt. Google verwendet IO, um Antworten auf Nutzersuchen anzubieten und anzuzeigen. Netflix empfiehlt damit Filme für den Abend. Und Facebook schlägt damit neue Freunde vor, die Sie vielleicht kennen.



Maschinelles Lernen war noch nie so wichtig und gleichzeitig so schwer zu erlernen. Dieser Bereich ist voller Fachsprache und die Anzahl der verschiedenen ML-Algorithmen wächst von Jahr zu Jahr.



Dieser Artikel führt Sie in grundlegende Konzepte des maschinellen Lernens ein. Insbesondere werden wir die Grundkonzepte der 9 wichtigsten ML-Algorithmen heute diskutieren.

Empfehlungssystem

Um ein vollständiges Empfehlungssystem aus 0 aufzubauen, sind fundierte Kenntnisse der linearen Algebra erforderlich. Aus diesem Grund kann es für Sie schwierig sein, einige der Konzepte in diesem Abschnitt zu verstehen, wenn Sie diese Disziplin noch nie studiert haben.



Aber keine Sorge - die Scikit-Learn-Python-Bibliothek macht es ziemlich einfach, einen CP zu erstellen. Sie benötigen also nicht diese tiefen Kenntnisse der linearen Algebra, um einen funktionierenden CP zu erstellen.

Wie funktioniert CP?

Es gibt zwei Haupttypen von Empfehlungssystemen:

• Inhaltsbasiert
• Kollaboratives Filtern

Ein inhaltsbasiertes System gibt Empfehlungen basierend auf der Ähnlichkeit der Elemente, die Sie bereits verwendet haben. Diese Systeme verhalten sich genau so, wie Sie es vom CP erwarten.



Die kollaborative CP-Filterung bietet Empfehlungen, die auf dem Wissen darüber basieren, wie der Benutzer mit Elementen interagiert (* Hinweis: Interaktionen mit Elementen anderer Benutzer, deren Verhalten dem Benutzer ähnlich ist, werden als Grundlage verwendet). Mit anderen Worten, sie verwenden die "Weisheit der Menge" (daher die "Zusammenarbeit" im Namen der Methode).



In der realen Welt ist die kollaborative CP-Filterung weitaus häufiger als ein inhaltsbasiertes System. Dies ist hauptsächlich auf die Tatsache zurückzuführen, dass sie normalerweise bessere Ergebnisse liefern. Einige Experten finden das kollaborative System auch leichter zu verstehen.



Die kollaborative CP-Filterung verfügt auch über eine einzigartige Funktion, die in einem inhaltsbasierten System nicht vorhanden ist. Sie haben nämlich die Möglichkeit, Funktionen selbst zu erlernen.



Dies bedeutet, dass sie möglicherweise sogar beginnen, Ähnlichkeiten in Elementen basierend auf Eigenschaften oder Merkmalen zu definieren, die Sie nicht einmal für das Funktionieren dieses Systems bereitgestellt haben.



Es gibt 2 Unterkategorien der kollaborativen Filterung:

• Modellbasiert
• Nachbarschaftsbasiert

Die gute Nachricht ist, dass Sie den Unterschied zwischen diesen beiden Arten der kollaborativen CP-Filterung nicht kennen müssen, um in ML erfolgreich zu sein. Es reicht zu wissen, dass es mehrere Arten gibt.

Zusammenfassen

Hier ist eine kurze Zusammenfassung dessen, was wir in diesem Artikel über das Empfehlungssystem gelernt haben:

• Beispiele für reale Empfehlungssysteme
• Verschiedene Arten von Empfehlungssystemen und warum kollaborative Filterung häufiger verwendet wird als inhaltsbasierte Systeme
• Die Beziehung zwischen Empfehlungssystem und linearer Algebra

Lineare Regression

Die lineare Regression wird verwendet, um einen y-Wert basierend auf einer Menge von x-Werten vorherzusagen.

Geschichte der linearen Regression

Die lineare Regression (LR) wurde 1800 von Francis Galton erfunden. Galton war ein Wissenschaftler, der die Verbindung zwischen Eltern und Kindern untersuchte. Insbesondere untersuchte Galton die Beziehung zwischen dem Wachstum der Väter und dem Wachstum ihrer Söhne. Galtons erste Entdeckung war die Tatsache, dass das Wachstum der Söhne in der Regel ungefähr dem Wachstum ihrer Väter entsprach. Was nicht überraschend ist.



Später entdeckte Galton etwas Interessanteres. Das Wachstum des Sohnes war in der Regel näher an der durchschnittlichen Gesamthöhe aller Menschen als am Wachstum seines eigenen Vaters.



Galton nannte dieses Phänomen Regression . Insbesondere sagte er: "Die Größe des Sohnes neigt dazu, sich zur durchschnittlichen Größe zurückzuziehen (oder sich in Richtung dieser zu verschieben)."



Dies führte zu einem ganzen Feld in Statistik und maschinellem Lernen, das als Regression bezeichnet wird.

Lineare Regressionsmathematik

Bei der Erstellung eines Regressionsmodells versuchen wir lediglich, eine Linie so nah wie möglich an jedem Punkt im Datensatz zu zeichnen.



Ein typisches Beispiel für diesen Ansatz ist der lineare Regressionsansatz der kleinsten Quadrate, bei dem die Nähe einer Linie in Auf-Ab-Richtung berechnet wird.



Beispiel zur Veranschaulichung:







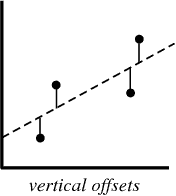
Wenn Sie ein Regressionsmodell erstellen, ist Ihr Endprodukt eine Gleichung, mit der Sie die y-Werte für den x-Wert vorhersagen können, ohne den y-Wert im Voraus zu kennen.

Logistische Regression

Die logistische Regression ähnelt der linearen Regression, außer dass anstelle der Berechnung des Werts von y ausgewertet wird, zu welcher Kategorie ein bestimmter Datenpunkt gehört.

Was ist logistische Regression?

Die logistische Regression ist ein maschinelles Lernmodell zur Lösung von Klassifizierungsproblemen.



Nachfolgend einige Beispiele für die Klassifizierungsaufgaben von MO:

• E-Mail-Spam (Spam oder nicht Spam?)
• Kfz-Versicherungsanspruch (Entschädigung oder Reparatur?)
• Diagnostik von Krankheiten

Jede dieser Aufgaben hat eindeutig zwei Kategorien, was sie zu Beispielen für binäre Klassifizierungsaufgaben macht.



Die logistische Regression eignet sich gut für binäre Klassifizierungsprobleme. Wir weisen 0 und 1 einfach unterschiedliche Kategorien zu.



Warum logistische Regression? Weil Sie keine lineare Regression für binäre Klassifizierungsvorhersagen verwenden können. Es funktioniert einfach nicht, da Sie versuchen, eine gerade Linie durch einen Datensatz mit zwei möglichen Werten zu ziehen.



Dieses Bild kann Ihnen helfen zu verstehen, warum lineare Regression für die binäre Klassifizierung schlecht ist:







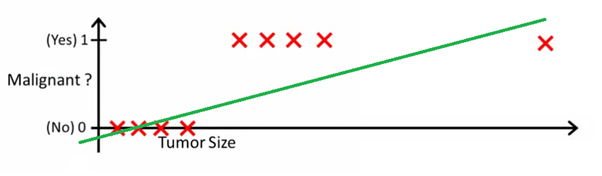
In diesem Bild repräsentiert die y-Achse die Wahrscheinlichkeit, dass der Tumor bösartig ist. Die 1-y-Werte geben die Wahrscheinlichkeit an, dass der Tumor gutartig ist. Wie Sie sehen können, ist das lineare Regressionsmodell für die Vorhersage der Wahrscheinlichkeit für die meisten Beobachtungen im Datensatz sehr schlecht.



Aus diesem Grund ist das logistische Regressionsmodell nützlich. Es hat eine Biegung in Richtung der Best-Fit-Linie, wodurch es viel besser für die Vorhersage qualitativer (kategorialer) Daten geeignet ist.



Hier ist ein Beispiel, das lineare und logistische Regressionsmodelle mit denselben Daten vergleicht:

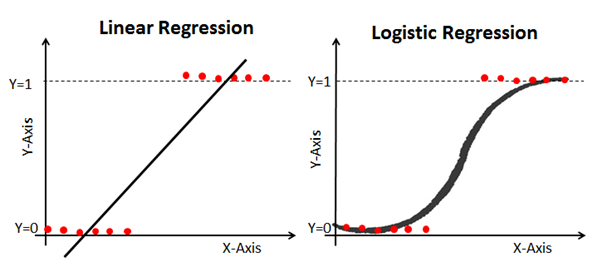
Sigmoid (Die Sigmoid-Funktion)

Der Grund, warum die logistische Regression geknickt ist, liegt darin, dass keine lineare Gleichung zur Berechnung verwendet wird. Stattdessen wird das logistische Regressionsmodell mithilfe eines Sigmoid erstellt (auch als logistische Funktion bezeichnet, da es in der logistischen Regression verwendet wird).



Sie müssen das Sigmoid nicht gründlich auswendig lernen, um in ML erfolgreich zu sein. Trotzdem ist es hilfreich, sich ein Bild von dieser Funktion zu machen.



Sigmoidformel: Das







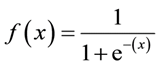
Hauptmerkmal eines Sigmoid, mit dem es sich zu befassen lohnt - unabhängig davon, welchen Wert Sie an diese Funktion übergeben, wird immer ein Wert zwischen 0-1 zurückgegeben.

Verwendung eines logistischen Regressionsmodells für Vorhersagen

Um die logistische Regression für Vorhersagen verwenden zu können, müssen Sie normalerweise den Grenzwert genau definieren. Dieser Grenzwert beträgt normalerweise 0,5.



Verwenden wir unser Beispiel für die Krebsdiagnose aus dem vorherigen Diagramm, um dieses Prinzip in der Praxis zu sehen. Wenn das logistische Regressionsmodell einen Wert unter 0,5 zurückgibt, wird dieser Datenpunkt als harmlos eingestuft. In ähnlicher Weise wird der Tumor als bösartig eingestuft, wenn das Sigmoid einen Wert über 0,5 ergibt.

Verwendung einer Fehlermatrix zur Messung der Wirksamkeit der logistischen Regression

Die Fehlermatrix kann als Werkzeug verwendet werden, um wahr-positive, wahr-negativ, falsch positiv und falsch negativ in MO zu vergleichen.



Die Fehlermatrix ist besonders nützlich, wenn die Leistung eines logistischen Regressionsmodells gemessen werden soll. Hier ist ein Beispiel, wie wir die Fehlermatrix verwenden können:







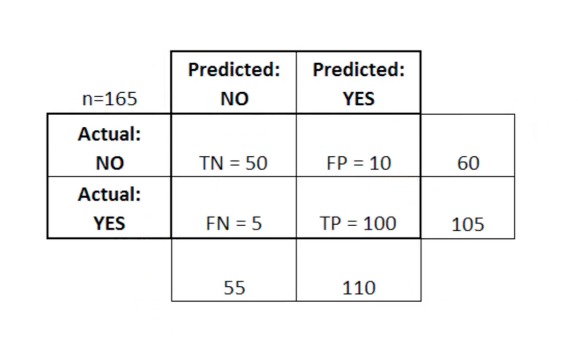
In dieser Tabelle steht TN für wahr-negativ, FN für falsch-negativ, FP für falsch-positiv, TP für wahr-positiv.



Eine Fehlermatrix ist nützlich für die Bewertung eines Modells, wenn die Fehlermatrix „schwache“ Quadranten enthält. Zum Beispiel kann sie eine ungewöhnlich hohe Anzahl von Fehlalarmen haben.



In einigen Fällen ist es auch sehr nützlich, sicherzustellen, dass Ihr Modell in einem besonders gefährlichen Bereich der Fehlermatrix ordnungsgemäß funktioniert.



In diesem Beispiel einer Krebsdiagnose möchten Sie beispielsweise sicherstellen, dass Ihr Modell nicht zu viele Fehlalarme aufweist, weil Dies bedeutet, dass Sie den bösartigen Tumor einer Person als gutartig diagnostiziert haben.

Zusammenfassen

In diesem Abschnitt haben Sie das ML-Modell - die logistische Regression - zum ersten Mal kennengelernt.

Hier ist eine kurze Zusammenfassung dessen, was Sie über logistische Regression gelernt haben:

• Arten von Klassifizierungsproblemen, die zur Lösung mit logistischer Regression geeignet sind
• Die logistische Funktion (Sigmoid) gibt immer einen Wert zwischen 0 und 1 an
• Verwendung von Grenzwerten zur Vorhersage mit einem logistischen Regressionsmodell
• Warum ist eine Fehlermatrix nützlich, um die Leistung eines logistischen Regressionsmodells zu messen?

K-Nearest Neighbors-Algorithmus

Der Algorithmus für k-nächste Nachbarn kann helfen, das Klassifizierungsproblem zu lösen, wenn mehr als 2 Kategorien vorhanden sind.

Was ist der Algorithmus für k-nächste Nachbarn?

Dies ist ein Klassifizierungsalgorithmus, der auf einem einfachen Prinzip basiert. Tatsächlich ist das Prinzip so einfach, dass es am besten ist, es anhand eines Beispiels zu demonstrieren.



Stellen Sie sich vor, Sie haben Größen- und Gewichtsdaten für Fußballer und Basketballspieler. Der Algorithmus für k-nächste Nachbarn kann verwendet werden, um vorherzusagen, ob ein neuer Spieler ein Fußballspieler oder ein Basketballspieler ist. Dazu ermittelt der Algorithmus die K Datenpunkte, die dem Untersuchungsobjekt am nächsten liegen.



Dieses Bild zeigt dieses Prinzip mit dem Parameter K = 3:







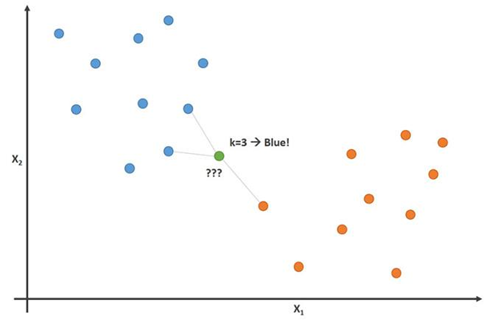
In diesem Bild sind Fußballspieler blau und Basketballspieler orange. Der Punkt, den wir zu klassifizieren versuchen, ist grün gefärbt. Da die meisten (2 von 3) Markierungen, die dem grünen Punkt am nächsten liegen, blau gefärbt sind (Fußballspieler), sagt der K-Nächste-Nachbarn-Algorithmus voraus, dass der neue Spieler auch ein Fußballspieler sein wird.

So erstellen Sie einen Algorithmus für K-nächste Nachbarn

Die Hauptschritte zum Erstellen dieses Algorithmus:

1. Sammeln Sie alle Daten
2. Berechnen Sie den euklidischen Abstand vom neuen Datenpunkt x zu allen anderen Punkten im Datensatz
3. Sortieren Sie die Punkte aus dem Datensatz in aufsteigender Reihenfolge des Abstands zu x
4. Sagen Sie die Antwort mit derselben Kategorie voraus wie die meisten K-Daten, die x am nächsten kommen

Bedeutung der K-Variablen im K-Nearest-Neighbour-Algorithmus

Obwohl dies von Anfang an nicht offensichtlich ist, ändert das Ändern des K-Werts in diesem Algorithmus die Kategorie, in die der neue Datenpunkt fällt.



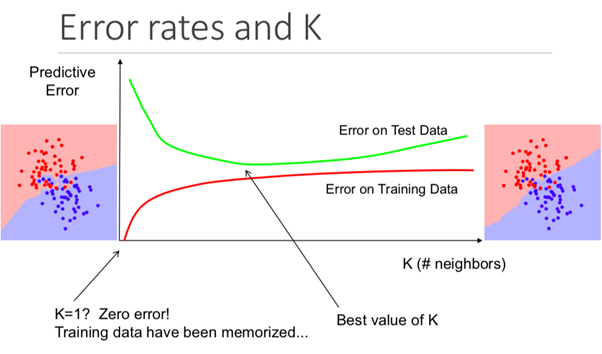
Insbesondere führt ein zu niedriger K-Wert dazu, dass Ihr Modell den Trainingsdatensatz genau vorhersagt, die Testdaten jedoch äußerst ineffektiv sind. Wenn Sie ein zu hohes K haben, wird das Modell unnötig komplex.



Die folgende Abbildung zeigt diesen Effekt perfekt:

Vor- und Nachteile des K-Nearest-Neighbour-Algorithmus

Um unsere Einführung in diesen Algorithmus zusammenzufassen, wollen wir kurz die Vor- und Nachteile seiner Verwendung diskutieren.



Vorteile:

• Der Algorithmus ist einfach und leicht zu verstehen
• Triviales Modelltraining mit neuen Trainingsdaten
• Funktioniert mit einer beliebigen Anzahl von Kategorien in einer Klassifizierungsaufgabe
• Fügen Sie einfach mehr Daten zu vielen Daten hinzu
• Das Modell akzeptiert nur 2 Parameter: K und die Entfernungsmetrik, die Sie verwenden möchten (normalerweise euklidische Entfernung).

Minuspunkte:

• Hohe Rechenkosten, weil Sie müssen die gesamte Datenmenge verarbeiten
• Funktioniert nicht so gut mit kategorialen Parametern

Zusammenfassen

Eine Zusammenfassung dessen, was Sie gerade über den K-Nearest Neighbor-Algorithmus gelernt haben:

• Ein Beispiel für ein Klassifizierungsproblem (Fußball- oder Basketballspieler), das der Algorithmus lösen kann
• Wie der Algorithmus den euklidischen Abstand zu benachbarten Punkten verwendet, um vorherzusagen, zu welcher Kategorie ein neuer Datenpunkt gehört
• Warum K-Werte für die Vorhersage wichtig sind
• Vor- und Nachteile der Verwendung des K-Nearest Neighbour-Algorithmus

Entscheidungsbäume und zufällige Wälder

Entscheidungsbaum und zufällige Gesamtstruktur sind zwei Beispiele für eine Baummethode. Genauer gesagt sind Entscheidungsbäume ML-Modelle, die zur Vorhersage verwendet werden, indem jede Funktion in einem Datensatz einzeln durchlaufen wird. Ein zufälliger Wald ist ein Ensemble (Komitee) von Entscheidungsbäumen, die zufällige Reihenfolgen von Objekten in einem Datensatz verwenden.

Was ist eine Baummethode?

Bevor wir uns mit den theoretischen Grundlagen der baumbasierten Methode in ML befassen, ist es hilfreich, mit einem Beispiel zu beginnen.



Stellen Sie sich vor, Sie spielen jeden Montag Basketball. Außerdem lädst du immer denselben Freund ein, mit dir zu spielen. Manchmal kommt ein Freund, manchmal nicht. Die Entscheidung, ob Sie kommen oder nicht, hängt von vielen Faktoren ab: Wetter, Temperatur, Wind und Müdigkeit. Sie bemerken diese Funktionen und verfolgen sie zusammen mit der Entscheidung Ihres Freundes, zu spielen oder nicht.



Sie können diese Daten verwenden, um vorherzusagen, ob Ihr Freund heute kommt oder nicht. Eine Technik, die Sie verwenden können, ist ein Entscheidungsbaum. So sieht es aus:







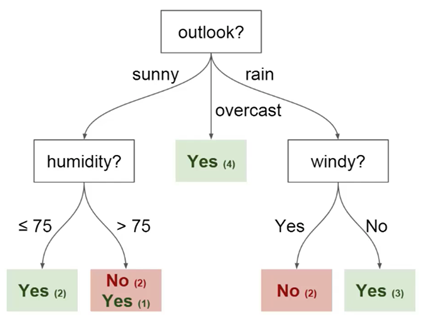
Jeder Entscheidungsbaum hat zwei Arten von Elementen:

• Knoten: Orte, an denen der Baum basierend auf dem Wert eines bestimmten Parameters aufgeteilt wird
• Kanten: Das Ergebnis der Aufteilung, die zum nächsten Knoten führt

Sie können sehen, dass das Diagramm Knoten für Ausblick, Luftfeuchtigkeit und

Wind enthält. Und auch die Facetten für jeden möglichen Wert jedes dieser Parameter.



Hier sind einige weitere Definitionen, die Sie verstehen sollten, bevor wir beginnen:

• Wurzel - der Knoten, von dem aus die Teilung des Baums beginnt
• Blätter - die endgültigen Knoten, die das Endergebnis vorhersagen

Sie haben jetzt ein grundlegendes Verständnis dafür, was ein Entscheidungsbaum ist. Wir werden uns im nächsten Abschnitt ansehen, wie man einen solchen Baum von Grund auf neu baut.

So erstellen Sie einen Entscheidungsbaum von Grund auf neu

Das Erstellen eines Entscheidungsbaums ist schwieriger als es sich anhört. Dies liegt daran, dass die Entscheidung, in welche Auswirkungen (Merkmale) Ihre Daten unterteilt werden sollen (was ein Thema aus Entropie und Datenerfassung ist), eine mathematisch herausfordernde Aufgabe ist.



Um dieses Problem zu lösen, verwenden ML-Spezialisten normalerweise viele Entscheidungsbäume und wenden zufällige Sätze von Merkmalen an, die ausgewählt wurden, um den Baum in sie zu unterteilen. Mit anderen Worten, für jeden einzelnen Baum an jeder separaten Partition werden neue zufällige Sätze von Merkmalen ausgewählt. Diese Technik nennt man zufällige Wälder.



Im Allgemeinen wählen Experten normalerweise die Größe eines zufälligen Satzes von Merkmalen (bezeichnet mit m) so, dass es die Quadratwurzel der Gesamtzahl der Merkmale im Datensatz ist (bezeichnet mit p). Kurz gesagt, m ist die Quadratwurzel von p, und dann wird eine bestimmte Eigenschaft zufällig aus m ausgewählt.

Vorteile der Verwendung eines zufälligen Waldes

Stellen Sie sich vor, Sie arbeiten mit vielen Daten, die eine "starke" Eigenschaft haben. Mit anderen Worten, in diesem Datensatz gibt es ein Merkmal, das hinsichtlich des Endergebnisses viel vorhersehbarer ist als andere Merkmale dieses Datensatzes.



Wenn Sie einen Entscheidungsbaum von Hand erstellen, ist es sinnvoll, dieses Merkmal für die oberste Partition in Ihrem Baum zu verwenden. Dies bedeutet, dass Sie mehrere Bäume haben, deren Vorhersagen stark korrelieren.



Wir wollen das vermeiden, weil Die Verwendung des Mittelwerts stark korrelierter Variablen verringert die Varianz nicht signifikant. Durch die Verwendung zufälliger Merkmalssätze für jeden Baum in einem zufälligen Wald dekorrelieren wir die Bäume und die Varianz des resultierenden Modells wird verringert. Diese Dekorrelation ist ein großer Vorteil bei der Verwendung zufälliger Wälder gegenüber handgefertigten Entscheidungsbäumen.

Zusammenfassen

Hier ist eine kurze Zusammenfassung dessen, was Sie gerade über Entscheidungsbäume und zufällige Wälder gelernt haben:

• Ein Beispiel für ein Problem, dessen Lösung mithilfe eines Entscheidungsbaums vorhergesagt werden kann
• Entscheidungsbaumelemente: Knoten, Flächen, Wurzeln und Blätter
• Wie die Verwendung eines zufälligen Satzes von Merkmalen es uns ermöglicht, einen zufälligen Wald zu erstellen
• Warum die Verwendung einer zufälligen Gesamtstruktur zur Dekorrelation von Variablen hilfreich sein kann, um die Varianz des resultierenden Modells zu verringern

Support-Vektor-Maschinen

Support-Vektor-Maschinen sind ein Klassifizierungsalgorithmus (obwohl sie technisch gesehen auch zur Lösung von Regressionsproblemen verwendet werden können), der einen Datensatz in Kategorien mit den größten "Lücken" zwischen Kategorien unterteilt. Dieses Konzept wird klarer, wenn Sie sich das folgende Beispiel ansehen.

Was ist eine Support-Vektor-Maschine?

Eine Support Vector Machine (SVM) ist ein überwachtes ML-Modell mit geeigneten Lernalgorithmen, die Daten analysieren und Muster erkennen. Das SVM kann sowohl für Klassifizierungsaufgaben als auch für Regressionsanalysen verwendet werden. In diesem Artikel werden wir uns speziell mit der Verwendung von Support-Vektor-Maschinen zur Lösung von Klassifizierungsproblemen befassen.

Wie funktioniert die Absichtserklärung?

Lassen Sie uns genauer untersuchen, wie die Absichtserklärung wirklich funktioniert.



Wir erhalten eine Reihe von Trainingsbeispielen, von denen jedes als zu einer von zwei Kategorien gehörend markiert ist. Mit dieser Reihe von SVMs erstellen wir ein Modell. Dieses Modell kategorisiert neue Beispiele in eine von zwei Kategorien. Dies macht die SVM zu einem unwahrscheinlichen binären linearen Klassifikator.



Die Absichtserklärung verwendet Geometrie, um Vorhersagen nach Kategorien zu treffen. Insbesondere bildet die Unterstützungsvektormaschine Datenpunkte als Punkte im Raum ab und kategorisiert sie so, dass sie durch eine möglichst große Lücke voneinander getrennt sind. Die Vorhersage, dass neue Datenpunkte zu einer bestimmten Kategorie gehören, basiert auf der Seite des Unterbrechungspunkts.



Hier ist ein Visualisierungsbeispiel, das Ihnen hilft, die Intuition der Absichtserklärung zu verstehen:







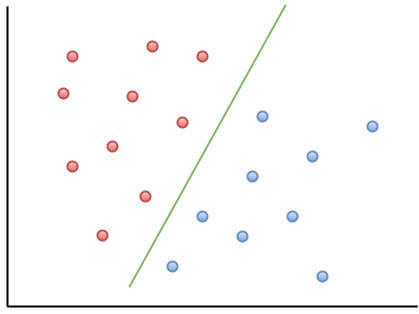
Wie Sie sehen können, wird ein neuer Datenpunkt, der links von der grünen Linie liegt, als „rot“ und rechts als „blau“ bezeichnet. Diese grüne Linie wird als Hyperebene bezeichnet und ist ein wichtiger Begriff für die Arbeit mit Absichtserklärungen.



Schauen wir uns die folgende visuelle Darstellung der SVM an:







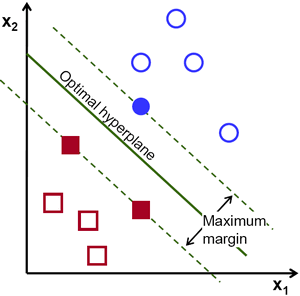
In diesem Diagramm wird die Hyperebene als "optimale Hyperebene" bezeichnet. Support Vector Machine-Theorie definiert eine optimale Hyperebene als Hyperebene, die das Feld zwischen den beiden nächstgelegenen Datenpunkten aus verschiedenen Kategorien maximiert.



Wie Sie sehen können, wirkt sich die Feldgrenze tatsächlich auf 3 Datenpunkte aus - 2 aus der roten Kategorie und 1 aus der blauen. Diese Punkte, die mit dem Feldrand in Kontakt stehen, werden als Unterstützungsvektoren bezeichnet - daher der Name.

Zusammenfassen

Hier ist eine kurze Momentaufnahme dessen, was Sie gerade über Support-Vektor-Maschinen gelernt haben:

• Die Absichtserklärung ist ein Beispiel für einen überwachten ML-Algorithmus
• Der Unterstützungsvektor kann sowohl zur Lösung von Klassifizierungsproblemen als auch zur Regressionsanalyse verwendet werden.
• Wie die Absichtserklärung Daten mithilfe einer Hyperebene kategorisiert, die den Abstand zwischen Kategorien im Datensatz maximiert
• Diese Datenpunkte, die die Grenzen des Teilungsfeldes berühren, werden als Unterstützungsvektoren bezeichnet. Hier kommt der Name der Methode her.

K-Means Clustering

Die K-Means-Methode ist ein unbeaufsichtigter Algorithmus für maschinelles Lernen. Dies bedeutet, dass Daten ohne Tags akzeptiert werden und versucht wird, Cluster ähnlicher Beobachtungen in Ihren Daten zu gruppieren. Die K-Means-Methode ist äußerst nützlich für die Lösung realer Anwendungen. Hier sind Beispiele für verschiedene Aufgaben, die zu diesem Modell passen:

• Kundensegmentierung für Marketingteams
• Klassifizierung von Dokumenten
• Optimierung der Versandwege für Unternehmen wie Amazon, UPS oder FedEx
• Identifizierung und Reaktion auf kriminelle Orte in der Stadt
• Professionelle Sportanalyse
• Vorhersage und Verhinderung von Cyberkriminalität

Das Hauptziel der K-Means-Methode besteht darin, den Datensatz in unterscheidbare Gruppen zu unterteilen, so dass die Elemente in jeder Gruppe einander ähnlich sind.



Hier ist eine visuelle Darstellung dessen, wie es in der Praxis aussieht:







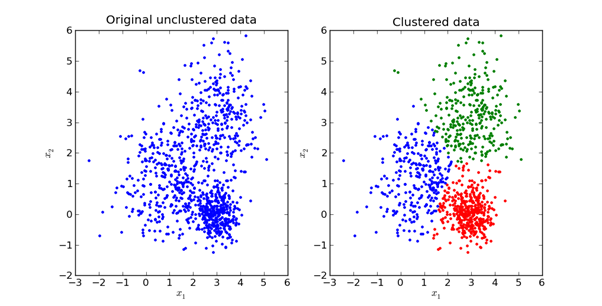
Wir werden die Mathematik hinter der K-Means-Methode im nächsten Abschnitt dieses Artikels untersuchen.

Wie funktioniert die K-Means-Methode?

Der erste Schritt bei der Verwendung der K-Means-Methode besteht darin, die Anzahl der Gruppen auszuwählen, in die Sie Ihre Daten aufteilen möchten. Diese Größe ist der Wert von K, der sich im Namen des Algorithmus widerspiegelt. Die Wahl des K-Wertes bei der K-Means-Methode ist sehr wichtig. Wir werden später diskutieren, wie Sie den richtigen K-Wert



auswählen . Als Nächstes müssen Sie einen Punkt im Datensatz zufällig auswählen und ihn einem zufälligen Cluster zuweisen. Dadurch erhalten Sie die Startdatenposition, an der Sie die nächste Iteration ausführen, bis sich die Cluster nicht mehr ändern:

• Berechnung des Schwerpunkts jedes Clusters anhand des mittleren Punktvektors in diesem Cluster
• Ordnen Sie jeden Datenpunkt dem Cluster zu, dessen Schwerpunkt dem Punkt am nächsten liegt

Auswahl eines geeigneten K-Werts in der K-Means-Methode

Genau genommen ist die Auswahl eines geeigneten K-Wertes ziemlich schwierig. Es gibt keine „richtige“ Antwort bei der Auswahl des „besten“ K-Werts. Eine Methode, die ML-Profis häufig verwenden, wird als „Ellbogenmethode“ bezeichnet.



Um diese Methode zu verwenden, müssen Sie zunächst die Summe der quadratischen Fehler berechnen - die Standardabweichung für Ihren Algorithmus für eine Gruppe von K-Werten. Die Standardabweichung bei der K-Mittelwert-Methode ist definiert als die Summe der Quadrate der Abstände zwischen den einzelnen Datenpunkten im Cluster. und der Schwerpunkt dieses Clusters.



Als Beispiel für diesen Schritt können Sie die Standardabweichung für die K-Werte 2, 4, 6, 8 und 10 berechnen. Als Nächstes möchten Sie ein Diagramm der Standardabweichung und dieser K-Werte erstellen. Sie werden sehen, dass die Abweichung mit zunehmendem K-Wert abnimmt.



Und es ist sinnvoll: Je mehr Kategorien Sie aus einem Datensatz erstellen, desto wahrscheinlicher ist es, dass sich jeder Datenpunkt nahe der Mitte des Clusters dieses Punkts befindet.

Vor diesem Hintergrund besteht die Hauptidee der Ellbogenmethode darin, den K-Wert zu wählen, bei dem der Effektivwert die Abnahmerate drastisch verlangsamt. Dieser starke Rückgang bildet einen „Ellbogen“ auf der Karte.



Als Beispiel ist hier eine Auftragung von RMS gegen K. In diesem Fall schlägt die Ellbogenmethode die Verwendung eines K-Werts von etwa 6 vor.







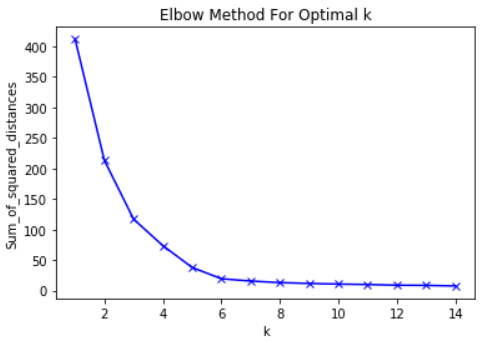
Es ist wichtig, dass K = 6 einfach eine Schätzung eines akzeptablen K-Werts ist. Es gibt keinen "besten" K-Wert in der K-Means-Methode. Wie viele Dinge in ML ist dies eine sehr situative Entscheidung.

Zusammenfassen

Hier ist eine kurze Skizze dessen, was Sie gerade in diesem Abschnitt gelernt haben:

• Beispiele für ML-Aufgaben ohne Lehrer, die mit der K-Means-Methode gelöst werden können
• Grundprinzipien der K-Mittel-Methode
• Wie K-Means funktioniert
• Verwendung der Ellbogenmethode zur Auswahl des geeigneten Werts für den K-Parameter in diesem Algorithmus

Hauptkomponentenanalyse

Die Hauptkomponentenanalyse wird verwendet, um einen Datensatz mit vielen Parametern in einen neuen Datensatz mit weniger Parametern umzuwandeln. Jeder neue Parameter in diesem Datensatz ist eine lineare Kombination zuvor vorhandener Parameter. Diese transformierten Daten rechtfertigen tendenziell einen Großteil der Varianz des ursprünglichen Datensatzes viel einfacher.

Was ist die Hauptkomponentenmethode?

Die Hauptkomponentenanalyse (PCA) ist eine ML-Technik, mit der die Beziehungen zwischen Variablensätzen untersucht werden. Mit anderen Worten, die PCA untersucht Sätze von Variablen, um die Grundstruktur dieser Variablen zu bestimmen. PCA wird manchmal auch als Faktoranalyse bezeichnet.



Basierend auf dieser Beschreibung könnten Sie denken, dass PCA der linearen Regression sehr ähnlich ist. Aber das ist nicht so. Tatsächlich weisen diese beiden Techniken mehrere wichtige Unterschiede auf.

Unterschiede zwischen linearer Regression und PCA

Die lineare Regression bestimmt die Linie der besten Anpassung im gesamten Datensatz. Die Hauptkomponentenanalyse identifiziert mehrere orthogonale Best-Fit-Linien für einen Datensatz.



Wenn Sie mit dem Begriff orthogonal nicht vertraut sind, bedeutet dies einfach, dass die Linien im rechten Winkel zueinander stehen, wie z. B. Nord, Ost, Süd und West auf einer Karte.

Schauen wir uns ein Beispiel an, um Ihnen zu helfen, dies besser zu verstehen.







Schauen Sie sich die Achsenbeschriftungen in diesem Bild an. Die Hauptkomponente der x-Achse erklärt 73% der Varianz in diesem Datensatz. Die Hauptkomponente der y-Achse erklärt etwa 23% der Varianz im Datensatz.



Dies bedeutet, dass 4% der Varianz ungeklärt bleiben. Sie können diese Anzahl reduzieren, indem Sie Ihrer Analyse weitere Hauptkomponenten hinzufügen.

Zusammenfassen

Eine Zusammenfassung dessen, was Sie gerade über die Hauptkomponentenanalyse gelernt haben:

• PCA versucht, orthogonale Faktoren zu finden, die die Variabilität in einem Datensatz bestimmen
• Unterschied zwischen linearer Regression und PCA
• Wie orthogonale Hauptkomponenten aussehen, wenn sie in einem Datensatz gerendert werden
• Das Hinzufügen zusätzlicher Hauptkomponenten kann dazu beitragen, die Varianz im Datensatz genauer zu erklären