
Andere Artikel im Zyklus
AES — . I
ES — . II
AES — . III
AES — . IV
AES — . V.
ES — . II
AES — . III
AES — . IV
AES — . V.
In diesem IV-Teil vervollständigen wir die Beschreibung der AES-128-Chiffre. Für Leser, die mit den vorherigen Teilen der Arbeit nicht vertraut sind, werde ich erklären, dass das Material zu Bildungszwecken präsentiert wird und dies eine Reihe von Merkmalen (Details, numerische Beispiele, mathematische Grundlagen usw.) auferlegt. Es ist nicht nur dazu gedacht, sich mit dem Standard vertraut zu machen und die Verwendung des vorgestellten Materials für die Entwicklung von Verschlüsselungs- und Entschlüsselungsalgorithmen (in Abwesenheit eines Schlüssels). Die Autoren vieler bekannter Online- (und Offline-) Veröffentlichungen haben sich solche Ziele nicht gesetzt, weshalb diese Veröffentlichungen für unsere Zwecke wenig nützlich sind.
Der umgekehrte Verschlüsselungsprozess wird als Nachrichtenentschlüsselung bezeichnet. Zum Entschlüsseln (mit einem Schlüssel) von Chiffretexten (ST) werden eine inverse Substitutionstabelle und runde Schlüssel erstellt, die in umgekehrter Reihenfolge zum Verschlüsselungsschema verwendet werden, jedoch dem Verschlüsselungsprozess ähnlich sind.
AES-Nachrichten entschlüsseln
Die Liste der Vorgänge zum Entschlüsseln einer Nachricht bleibt dieselbe wie für die Verschlüsselung. Weitere Details zum Betrieb finden Sie hier . Dies ist ein ziemlich allgemeines Prinzip von Chiffren - eine einzige Hardware-Implementierung für die Ver- und Entschlüsselung, die durch Sätze derselben Funktionen für beide Prozesse bereitgestellt wird. Nur der Quelltext und die Reihenfolge der Schlüsselübermittlung werden geändert.
Der Prozess des Entschlüsselns von Nachrichten wird als eine Folge von für die Verschlüsselung verwendeten umgekehrten (inversen) Transformationen in der umgekehrten Reihenfolge ihrer Reihenfolge während der Verschlüsselung implementiert. Es ist auch offensichtlich, dass die runden Schlüssel in der entsprechenden Reihenfolge verwendet werden: zuerst der zuletzt empfangene Schlüssel, dann der vorletzte Schlüssel usw. bis zum ersten runden Schlüssel.
Alle Transformationsnamen bleiben gleich, jedoch wird Inv vorangestellt. Wir werden sie in der gleichen Reihenfolge wie zuvor betrachten. Die AES-Verschlüsselung ermöglicht zwei Entschlüsselungsoptionen, Rückwärts und Vorwärts, die nachstehend ausführlich erläutert werden.
Option zur umgekehrten Entschlüsselung
Die umgekehrte Entschlüsselung einer Nachricht ist ein natürlicher Vorgang zum Umkehren des Verschlüsselungsprozesses.
Die AddRoundKey-Operation bleibt für alle 16 Bytes des Status das gleiche (unveränderte) S + Ki wie beim Verschlüsseln der Nachricht, d. H. ist das Gegenteil von sich. Dies liegt an der Tatsache, dass in der Operation XOR-Logik verwendet wird und Bytes in Binärzahlen darstellbar sind.
Der Schlüssel der letzten Runde wird einfach zur verschlüsselten Nachricht hinzugefügt (zusammengefasst).
InvSubBytes. Das Wesen dieser Transformation hat sich nicht geändert, d. H. Jedes Byte der zu konvertierenden Nachricht wird durch ein anderes ersetzt, das aus der Tabelle (S & supmin; ¹) entnommen wurde-block) Ersatz. Natürlich ist die Substitutionstabelle hier anders. Das Byte {x, y} wird nach dem gleichen Prinzip durch das Byte aus Inv S (x, y) ersetzt: x - Tabellenzeile, y - Spalte. Das Ersatzbyte wird aus der Zelle am Schnittpunkt von Zeile (x) und Spalte (y) der Inv S (x, y) -Tabelle abgerufen.
Wie zuvor beträgt die Größe der Tabelle 16 × 16 = 256 Bytes, von denen jedes durch Vektormatrixmultiplikation und -subtraktion (affine Transformation) vom Produkt des Verschiebungsvektors C erhalten wird. In binären Feldern sind die Additions- und Subtraktionsoperationen äquivalent, so dass der Vektor C einfach addiert werden kann Produkt. Die InvSubBytes-Tabelle wird unten angezeigt. Der angegebene Substitutionsknoten S -1 ist in der folgenden Tabelle 1 dargestellt, die Werte sind im hexadezimalen Format angegeben:
Tabelle 1. Substitutionstabelle des inversen S -1 - Blocks

Die Tabelle zeigt Beispiele für das Ersetzen von zwei mit Grün gefüllten Bytes 4A → 5C und 9F → 6E.
InvShiftRows. Diese Transformation verschiebt die Zeilen in der Tabelle (das Zustandsquadrat) nach rechts (in die der ursprünglichen Verschiebung entgegengesetzte Richtung). Der Verschiebungswert für jede Zeile bleibt gleich: Die erste (obere) Zeile wird nicht um c0 = 0 verschoben, die zweite um c1 = 1, die nächste um c2 = 2 und die letzte um c3 = 3 Positionen (Zellen). Die Werte c0, c1, c2, c3 wurden in der Tabelle und in der vorherigen Abbildung für die erste Runde der Nachrichtenkonvertierung angegeben.

Das Ergebnis einer solchen Multiplikation in der Skalardarstellung ist:
S'0C = ({0l} · S0C) {({0b} · S1C) ⊕ ({0d} · S2C) ⊕ ({09} · S3C);
S'1C = ({09} S0C) {({0l} S1C) ⊕ ({0b} S2C) ⊕ ({0d} S3C);
S'2C = ({0d} S0C) ⊕ ({09} S1C) ⊕ ({0l} S2C) ⊕ ({0b} S3C);
S'3C = ({0b} S0C) ⊕ ({0d} S1C) ⊕ ({09} S2C) ⊕ ({0l} S3C).
Um IT von PCs zu erhalten, verwendet der Entschlüsselungsalgorithmus dieselben Parameterwerte, die beim Verschlüsselungsprozess verwendet wurden. Die Regeln zum Generieren des erweiterten Schlüssels bleiben unverändert.
Direkte Entschlüsselungsoption
Die Merkmale des Entschlüsselungsalgorithmus für einige inverse Transformationen ermöglichen es, die gleiche Reihenfolge von Operationen wie beim Verschlüsselungsalgorithmus beizubehalten, jedoch erfordern einige der Parameterwerte Änderungen. Zunächst sprechen wir über den Schlüssel (seine Entfaltung).
Untersuchungen haben gezeigt, dass die Reihenfolge der Funktionen SubBytes () und ShiftRows () den Wert des Ergebnisses nicht ändert, dh diese Funktionen sind durchlässig (sie pendeln). Diese Position (Eigenschaft) gilt auch für die Funktionen InvSubBytes (), InvShiftRows (). Dieses Muster ist leicht zu erklären. Der Punkt ist, dass beide Funktionen mit ganzzahligen Bytes arbeiten und die Verschiebungen durch ein ganzzahliges Vielfaches eines Bytes ausgeführt werden und den Wert der Bytes selbst nicht ändern.
Beachten Sie Folgendes zur Operation MixColumns (). Es ist linear zu den Eingangsbytes (Daten).
InvMixColumns (State XOR Round Key) = InvMixColumns (State) XOR
InvMixColumns (Round Key).
Diese Merkmale von Funktionen (Eigenschaften) ermöglichen das Ändern der Reihenfolge ihrer Anwendung, d. H.
InvSubBytes (InvShiftRows ()) = InvShiftRows (InvSubBytes ()).
AddRoundKey (InvMixColumns ()) = InvMixColumns (AddRoundKey ()),
vorausgesetzt, die Spalten (32-Bit-Wörter) des erweiterten Entschlüsselungsschlüssels wurden zuvor über die Funktion
InvMixColumns () übergeben.
Das Vorstehende bedeutet, dass die Art der Entschlüsselung des PCs wirksam gemacht werden kann, indem die Reihenfolge der Verwendung der für die Verschlüsselung übernommenen Funktionen beibehalten wird. In diesem Fall werden natürlich die Kosten für die Hardware- und Software-Implementierung der Verschlüsselung erheblich reduziert. Die Änderungen betreffen nur das Verfahren zum Generieren der Schlüsselbereitstellung.
In der InvMixColumns () -Funktion müssen Sie den Typ der Variablen konvertieren, der Eingabeparameter der Funktion ist ein zweidimensionales Byte-Array (Quadrat) und der erweiterte Schlüssel wird als lineares (String-) Array aus 32-Bit-Wörtern gebildet. Aus diesem Grund ist es erforderlich, eine Typanpassung an das Quadrat durchzuführen.
Lassen Sie uns am Beispiel einer 2-Runden-Transformation zwei äquivalente Versionen des RIJNDAEL-Entschlüsselungsverfahrens zeigen. Die erste Option ist die übliche Umkehrung der Verschlüsselungsfunktion. Die zweite Option ergibt sich aus der ersten, indem die Reihenfolge der Operationen in drei Transformationspaaren
InvShi ftRows () → InvSubBytes () zweimal und
AddRoundKey () → InvMixColumns () 1 Mal geändert wird.
Das Ergebnis der Transformation wird gespeichert, wenn
in den angegebenen Paaren vom Original zur umgekehrten Abfolge von Operationen übergegangen wird.
Aus der Tabelle geht hervor, dass die Verschlüsselungsprozedur und die zweite Variante der Entschlüsselungsprozedur bis zur Reihenfolge der Verwendung von runden Schlüsseln (bei der Ausführung von AddRoundKey-Operationen), Ersatztabellen (bei der Ausführung von SubBytes () - und InvSubBytes () -Operationen) und Transformationsmatrizen (bei der Ausführung von MixColumns () zusammenfallen ) und InvMixColumns ()).
Tabelle 2 - Reihenfolge der Transformationen in der Zwei-Runden-Version von RIJNDAEL

Ein ähnliches Ergebnis gilt für eine beliebige Anzahl von Runden.
Wiederherstellen eines Chiffrierschlüssels mit dem letzten Unterschlüssel
Generierung runder AES-Chiffrierschlüssel. Der Schlüsselplan zum Generieren von runden Schlüsseln aus einem 128-Bit-Originalverschlüsselungsschlüssel ist eine rekursive Funktion. Diese Funktion wird hier ausführlich besprochen . Die Anfangsbedingungen für seinen Start sind die ersten 4 4-Byte-Wörter des Schlüssels (4 × 32-Bit-Wörter), dh W [0], W [1], W [2], W [3]. Formulieren
wir das Problem der Wiederherstellung dieses 128-Bit-Chiffrierschlüssels wie folgt: Lassen Sie die Komponenten des runden 10-Runden-Schlüssels W [43], W [42], W [41], W [40] gefunden werden.
Es ist erforderlich, den vollständigen Chiffrierschlüssel nur mit diesem runden Schlüssel wiederherzustellen.
Es ist zweckmäßig, die Lösung des Problems zuerst anhand numerischer Daten zu betrachten. Nehmen wir als Grundlage das in FIPS PUB 197 angegebene numerische Beispiel.. Tabelle 3 enthält den Schlüssel für Runde 10.
Das Verfahren zum Erzeugen runder Schlüssel ist so organisiert, dass es eine Vorwärtsbewegung (Entfalten des Schlüssels) entlang einer Reihe vorheriger Schlüsselwerte ermöglicht. Um von einem Punkt einer Reihe von Werten rückwärts zu gehen, müssen die Anfangsdaten des Berechnungsprozesses an diesem Punkt der Rückkehr vorliegen. Der Rückgabepunkt sei der letzte Schritt der letzten 10. Runde, d. H. Vier 4-Byte-Wörter des Schlüssels der 10. Runde Nk = Nb = 4 sind bekannt.
Tabelle 3 - 128-Bit-Schlüssel der 10. Runde der AES-Chiffre

Ferner werden die Ergebnisse und Aktionen des Schlüsselwiederherstellungsalgorithmus platziert Bequemlichkeit in Tabelle 4, die einer (Art umgestürzten) Schlüsselgenerierungstabelle ähnelt.
Tabelle 4 - Wiederherstellung des Chiffrierschlüssels aus dem bekannten Schlüssel der 10. Runde

Erläuterungen zu Tabelle 4. Die Rundenzahlen werden vom 10. bis zum 1. in umgekehrter Reihenfolge gezählt. Drei Spalten (3, 8, 9) der Tabelle enthalten vorgefertigte Schlüssel mit unterschiedlichen aktuellen Nummern, abhängig von der i-Zeilennummer. Die übrigen Zellen enthalten Hilfsdaten für Zwischenberechnungen. Somit erscheint der Wert des Schlüssels W [i] dreimal in der Tabelle in drei Spalten.
Die Spalten 1 und 2 sind die Nummer r der Runde und die Ordnungszahl i des 4-Byte-Schlüsselworts. Das letzte derartige Wort während der Verschlüsselung hat die Nummer i = 43. In der Tabelle schreiben wir es in die oberste Zeile der rechten (9) Spalte. Die Zahlen i der Zeilen der Tabelle nehmen ab und in Spalte 9 entsprechen sie den Wörtern des Schlüssels W [i]. Die 8. Spalte enthält das Wort W [i - Nk] des Schlüssels mit einer reduzierten Zahl W [43 - 4] = W [39] und die 3. Spalte - das Schlüsselwort W [i - 1] = W [42]. vorheriges W [i] = W [43].
Die Bedeutung des Wortes W [39] in der 8. Spalte ist unbekannt und wird aus den Anfangsdaten anhand der Formel ermittelt:
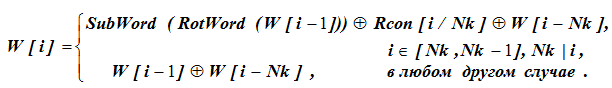
Bei Formelberechnungen werden zunächst die Bedingungen für die Auswahl der Formelzeile überprüft. Für W [43] ist i = 43 und Nk teilt den Wert 43 nicht vollständig, dh für i = 43 wird der Wert von W [i] durch die untere Zeile der Formel bestimmt: W [43] = W [42] W [39]. Hier ist für die gegebenen Werte von W [42] und W [43] der letzte Term W [39] nicht definiert.
Dann ist W [39] = W [43] W [42] = b6630ca6 - e13f0cc8.
In der binären Arithmetik mod2 sind Additions- und Subtraktionsoperationen äquivalent, daher haben bitweise Berechnungen für jedes der 4 Bytes des Schlüsselworts W [39] die Form (Tabelle 5):
Tabelle 5 - Byte-Berechnungen des Schlüsselworts W [39].

Somit wurde der Wert des Schlüsselworts W [39] = 575c006e gefunden. Wir übertragen diesen Wert in die 3. Spalte, in die Zeile i = 40 und in die 9. Spalte in die
Zeile i = 39. Die Berechnungen in der Zeile i = 40 werden wie beim Erweitern des Schlüssels ausgeführt.
Das unbekannte Wort W [i - Nk] = W [40 - Nk] = W [i = 36] sollte wie im vorherigen Fall durch die Differenz W [36] = W [40] 7 Spalte der Zeile 40 bestimmt
werden. Der Wert in 7- Die dritte Spalte der Zeile 40 wird als Summe (OR) der 5. und 6. Spalte gebildet. Der Wert der 5. Spalte wird aus W [39] nach einer zyklischen RotWord-Verschiebung (4. Spalte) und einer SubWord-Ersetzungsoperation (5. Spalte) erhalten.
Die Ergebnisse dieser Aktionen haben die Form
RotWord (575c006e) = 5c006e57; Unterwort (5c006e57) = 4a639f5b.
Der Wert in der 6. Spalte wird als Konstante erhalten
Rcon [j = i / Nk] = Rcon [j = 40/4] = 2 j-1 = 2 9 .
Diese Konstante wird durch ein hexadezimales Byte
2 9 ≈ 100000000 = x 9 dargestellt , aber es gibt kein solches Byte im Feld GF (2 8 ): Sie müssen den Rest der Division durch ein irreduzibles Polynom finden, d. H.
Nachdem wir die Konstante in das Schlüsselwort aufgenommen haben, haben wir
Rcon [j = 40 / Nk] = 36000000 (6. Spalte). Der Wert der 7. Spalte wird erhalten als (7. Spalte) = (5. Spalte) ⊕ (6. Spalte) = 4a639f5b⊕36000000 = 7c639f5b.
Und schließlich gilt für
W [36] = W [40] (7. Spalte der Zeile 40) = d014f9a8 7c639f5b = ac7766f3.
Weitere analoge Berechnungen führen zum Endergebnis - dem Chiffrierschlüssel.
Weitere Informationen zu den Funktionen w und RotWord, Rcon und SubWord. Angenommen, wir bezeichnen mit Kr [j] - dem j-ten Byte des r-ten runden Schlüssels und w [i] wie in der Dokumentation.
Wir erhalten: Kr = (w [Nk ∙ r], w [Nk ∙ r + 1], · · ·, w [Nk ∙ r + Nk - 1]).
Für verschiedene i haben wir die folgenden Beziehungen
für i ≠ 0 mod Nk, Nk ≤ i <Nb ∙ (Nr + 1), w [i] = w [i - Nk] x oder w [i - 1] und
für i = 0 mod Nk ist w [i] = w [i - Nk] x oder Unterwort (RotWord (w [i - 1])) xorRcon [i / Nk].
Daher ist für i ≤ 0modNk, Nk 0 ≤ i <Nb ≤ (Nr + 1) –Nk, w [i] = w [i + Nk] xor w [i + Nk - 1] und für i = 0modNk, w [i] = w [i + Nk] xorSubWord (RotWord (w [i + Nk - 1])) xorRcon [i + Nk / Nk]
Mit AES-256 müssen Sie eine Unterwortoperation hinzufügen, wenn i mit 4mod Nk vergleichbar ist. Es ist also möglich, den vorherigen Schlüssel vom letzten Unterschlüssel abzuleiten und Schritt für Schritt den Wert K0 des Chiffrierschlüssels zu erhalten.
Die mathematischen Grundlagen der AES - 128 Chiffre sind ganz vollständig und detailliert hier .
Wenden wir uns der Feldabbildung zu ℓ: GF (2 8 ) → GF (2 8 ); x → x 2 + x. Das Bild dieser Karte
1 = Im (l) hat die Dimension dim GF (2) (1) = 7.
Gleichung x2 + x = θ, wobei θ 1 zwei verschiedene Lösungen (Wurzeln der Gleichung) 1, 2є GF (2 8 ) hat.
Nach dem Satz von Vieta, x1⊕x2 = 1, ist die Summe der Wurzeln gleich dem Koeffizienten der Gleichung bei x 2 mit dem entgegengesetzten Vorzeichen, und das Produkt der Wurzeln x1⊗x2 = θ ist gleich dem freien Term der Gleichung (in unserer Gleichung mit dem entgegengesetzten Vorzeichen).
Es ist bekannt, dass in der Arithmetik von Binärfeldern die Operationen der Addition und Subtraktion der Elemente mod2 äquivalent sind.

Somit werden die Wurzeln der Gleichung durch das Verhältnis x2 = x1⊕1 in Beziehung gesetzt, da der Koeffizient bei x in der Gleichung 1 ist. Dies bedeutet, dass sie in der Dezimaldarstellung der Feldelemente in ihrer lexikografischen Reihenfolge nacheinander angeordnet sind und sich nur um eins unterscheiden.
Für x = 0 und x = 1 und für x = 2 und x = 3 erhalten wir also:

Die Ergebnisse (Bilder) der Abbildung in den reduzierten Paaren (0, 1); (2, 3) stimmte vollständig überein, d.h. Zwei Typen entsprechen einem Bild. Folglich ist die Kardinalität des Bildes zweimal kleiner als die Kardinalität des Vorbilds und seine Dimension seiner Elemente ist 7.
Das Produkt von Wurzelpaaren, dh der freie Term einer quadratischen Gleichung, wird zweckmäßigerweise durch die Potenzdarstellung der Elemente des Feldes bestimmt (inverse Bilder). In diesem Fall werden die Exponenten mod255 summiert, d.h. Modulo die Reihenfolge der multiplikativen Gruppe des Feldes GF (2 8 ).