Ich erinnere mich, dass ich eines Tages das Foto oben auf Flickr gesehen und mir das Gehirn gebrochen habe, um herauszufinden, was daran falsch war. Der Punkt war, dass sich der Propeller zu dem Zeitpunkt drehte, als der Bewegungssensor in der Kamera "Messwerte las", dh während der Belichtung der Kamera gab es eine gewisse Bewegung. Es lohnt sich wirklich darüber nachzudenken, lassen Sie uns gemeinsam darüber nachdenken.
Viele Digitalkameras verwenden heutzutage einen CMOS-Sensor als "Erfassungs" -Gerät, auch als aktiver Pixelsensor bekannt.Dies funktioniert durch Akkumulieren elektronischer Ladung, wenn Licht darauf trifft. Nach einer bestimmten Zeit - Belichtungszeit - wird die Ladung Zeile für Zeile zur weiteren Verarbeitung zurück zur Kamera übertragen. Die Kamera scannt dann das Bild und behält die Pixelreihen Zeile für Zeile bei. Das Bild wird verzerrt, wenn sich während der Aufnahme etwas bewegt. Stellen Sie sich zur Veranschaulichung vor, Sie schießen einen rotierenden Propeller. In den folgenden Animationen entspricht die rote Linie der aktuellen Leseposition und der Propeller dreht sich beim Lesen weiter. Der Teil unter der roten Linie ist das resultierende Bild.
Der erste Propeller macht während der Belichtung 1/10 Umdrehung:
Abonnieren Sie die Kanäle:
@Ontol - die interessantesten Texte / Videos aller Zeiten und Völker, die das Bild der Welt beeinflussen
@META LEARNING - wo ich meine nützlichsten Erkenntnisse über Bildung und die Rolle von IT / Spielen in der Bildung (sowie Antons Gedanken zu diesem Thema) teile Makarenko, Seymour Papert, Paul Graham, Joseph Licklider und Alan Kay)
Das Bild ist leicht verzerrt, aber nichts kritisches. Der Propeller bewegt sich jetzt zehnmal schneller und dreht sich während der Belichtung vollständig:
Das sieht schon aus wie das Bild, das wir am Anfang gesehen haben. Fünfmal pro Exposition:
Das ist schon etwas zu viel, also kannst du von den Rollen gehen. Lassen Sie uns Spaß haben und prüfen, wie unterschiedliche Objekte bei unterschiedlichen Rotationsgeschwindigkeiten pro Belichtung aussehen.
Genau der gleiche Propeller:
Große Propellerblätter:
Autoreifen:
Wir können den Rolling-Shutter-Effekt als eine Art Transformation der Koordinaten eines realen Objekts vom "Objektraum" in den "Bildraum" eines verzerrten Objekts wahrnehmen . Die folgende Animation zeigt, was mit dem kartesischen Koordinatensystem passiert, wenn die Anzahl der Umdrehungen zunimmt. Bei niedrigen Geschwindigkeiten ist die Verformung unbedeutend - die Zahl steigt auf eins, und jede Seite des Koordinatensystems bewegt sich nacheinander zur rechten Seite des Bildes. Dies ist eine ziemlich komplexe Transformation, die zu erfassen, aber leicht zu verstehen ist.
Das Bild sei I (r, θ), das reale (rotierende) Objekt sei f (r, θ), wobei (r, θ) 2D-Polarkoordinaten sind. Aufgrund der Rotationsbewegung der Objekte haben wir für diese Aufgabe Polarkoordinaten gewählt.
Das Objekt dreht sich mit einer Winkelfrequenz ω und der Verschluss bewegt sich mit einer Geschwindigkeit v vertikal entlang des Bildes. An der Position (r, θ) im Bild beträgt die Entfernung, die der Verschluss seit Beginn der Belichtung zurückgelegt hat, y = rsinθ, wobei die seit diesem Moment verstrichene Zeit (rsinθ) / v beträgt. Während dieser Zeit drehte sich das Objekt um (ω / v) rsinθ) Bogenmaß. Wir erhalten also
I (r, θ) = f (r, θ + (ω / v) rsinθ),
was die erforderliche Transformation ist. Das ω / v-Verhältnis ist proportional zur Anzahl der Umdrehungen pro Belichtung und parametrisiert die Transformation.
Um ein tieferes Verständnis der offensichtlichen Propellerformen zu erhalten, können wir ein Objekt betrachten, das aus P Propellern besteht, wobei f nur für
θ = 2π / P ungleich Null ist , 4π / P… 2π = 2pπ / P für 1 <p <P.
Bild I ist ungleich Null für θ + (ω / v) rsinθ = 2pπ / P oder
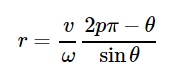
Im kartesischen Koordinatensystem wird es
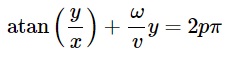
und hilft uns bei der Erklärung des Grundes, warum die Propeller eine S-Form annehmen - es ist einfach eine Funktion des Arkustangens im Bildraum. Cool. Unten habe ich diese Funktion mit einem Satz von fünf Propellerblättern mit leicht unterschiedlichen Anfangsversätzen aufgezeichnet. Sie können dies in der Wiedergabe sehen. Sie sind den Formen in den obigen Animationen sehr ähnlich.
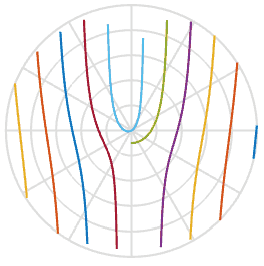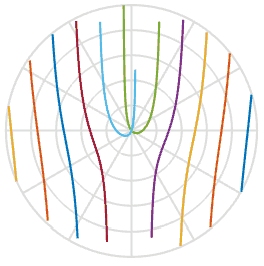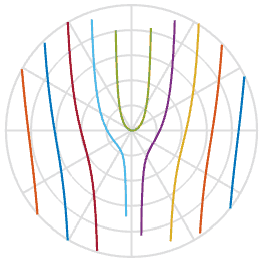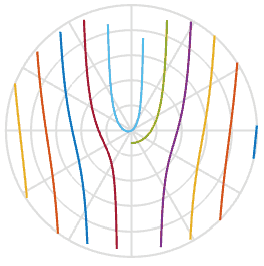
Können wir die beschädigten Fotos reparieren, da wir etwas mehr über den Vorgang erfahren haben? Mit einem der obigen Bilder kann ich eine Linie ziehen, zurückdrehen und diese Pixel in das neue Bild einfügen. In der folgenden Animation scanne ich das mit einer roten Linie markierte Bild links und drehe dann die Pixel entlang dieser Linie, um ein neues Bild zu erhalten. Auf diese Weise können wir das Bild eines realen Objekts wiederherstellen, auch wenn plötzlich ein nerviger Rolling Shutter Ihr Foto verdirbt.
Wenn ich in Photoshop besser wäre, würde ich die Propeller aus dem Originalfoto auf Flickr extrahieren, bearbeiten und wieder in das Foto einfügen. Ich glaube ich weiß was ich in Zukunft tun werde.
Wenn Sie die tatsächliche Anzahl der Klingen auf dem Foto zu Beginn des Beitrags und die Rotationsgeschwindigkeit wissen möchten, können Sie diesen ausgezeichneten Tumblr-Beitrag von Daniel Walsh lesen , in dem er eine mathematische Erklärung liefert.
Er glaubt, wir können die Anzahl der Klingen zählen, indem wir die "unteren" Klingen von den "oberen" subtrahieren, sodass wir drei Klingen in diesem Bild erhalten. Wir wissen auch, dass sich der Propeller während der Belichtung etwa zweimal dreht. Wenn wir also versuchen, die Drehung mit verschiedenen Geschwindigkeiten rückgängig zu machen, erhalten wir ungefähr Folgendes:
Ich musste herausfinden, wo sich die Mitte des Propellers befand, also zeichnete ich einen Kreis. Anscheinend sollte das Zentrum irgendwo in der Nähe sein. Leider fehlt ein Blade, aber es gibt genügend Informationen, um es anzuzeigen.
Ich habe die Stelle gefunden, an der sich alles am meisten schneidet. Bei dieser Drehzahl (2,39 Umdrehungen pro Belichtung) sehen das Originalbild und die Klingen folgendermaßen aus:
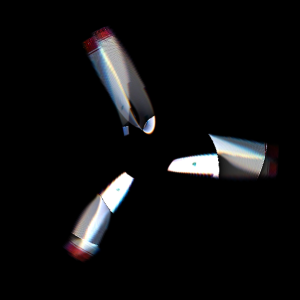
Leider ist das Bild nicht perfekt, aber zumindest sehr realitätsnah.
Über den Autor: Jason Cole ist ein Doktorand aus London, der sich leidenschaftlich für Mathematik, Physik und Datenvisualisierung interessiert. Hier ist seine Website . Und der Artikel wurde hier veröffentlicht .
Hacker News Diskussion
hinzufügen. Video
Abonnieren Sie die Kanäle:
@Ontol - die interessantesten Texte / Videos aller Zeiten und Völker, die das Bild der Welt beeinflussen
@META TRAINING , wo ich meine nützlichsten Erkenntnisse über Bildung und die Rolle von IT / Spielen in der Bildung (sowie Antons Gedanken zu diesem Thema) teile Makarenko, Seymour Papert, Paul Graham, Joseph Licklider und Alan Kay)
Erfahren Sie, wie Sie einen begehrten Beruf von Grund auf neu erlernen oder Ihre Fähigkeiten und Ihr Gehalt verbessern können, indem Sie bezahlte Online-Kurse von SkillFactory absolvieren:
- Kurs für maschinelles Lernen (12 Wochen)
- Data Science von Grund auf lernen (12 Monate)
- Analytics-Beruf mit jedem Startlevel (9 Monate)
- Python für Webentwicklungskurs (9 Monate)