Heap-Sortierung

Dies ist der letzte Artikel in einer Reihe über das Sortieren von Heaps. In früheren Vorlesungen haben wir uns mit einer Vielzahl von Heap-Strukturen befasst, die hinsichtlich der Geschwindigkeit hervorragende Ergebnisse erzielen. Dies wirft die Frage auf: Welcher Haufen ist beim Sortieren am effizientesten? Die Antwort lautet: die, die wir uns heute ansehen werden.

EDISON .




— « » — -, CRM-, , iOS Android.



;-)

Die ausgefallenen Haufen, die wir uns zuvor angesehen haben, sind in Ordnung, aber der effizienteste Haufen ist der Standardhaufen mit verbessertem Clearing.



Was wird gesiebt, warum wird es auf dem Haufen benötigt und wie funktioniert es - beschrieben im allerersten Teil einer Artikelserie.



Das Standard-Sieben in der klassischen Sortierung nach einem Bündel funktioniert ungefähr "Stirn" - ein Element aus der Wurzel des Teilbaums wird in die Zwischenablage gesendet, Elemente aus dem Zweig steigen nach den Ergebnissen des Vergleichs nach oben. Es ist einfach genug, aber es gibt zu viele Vergleiche.







In der aufsteigenden Spur werden Vergleiche gespeichert, da Eltern kaum mit ihren Nachkommen verglichen werden, im Grunde werden nur Nachkommen miteinander verglichen. In einem gewöhnlichen Heapsort werden sowohl die Eltern als auch die Kinder miteinander verglichen - daher gibt es fast eineinhalb Mal mehr Vergleiche mit der gleichen Anzahl von Austauschen.



Schauen wir uns also ein bestimmtes Beispiel an. Angenommen, wir haben ein Array, in dem ein Heap bereits fast gebildet ist - alles, was bleibt, ist, die Wurzel zu sieben. Für alle anderen Knoten ist die Bedingung erfüllt - jeder Nachkomme ist nicht mehr als sein Elternteil.



Zunächst müssen Sie von dem Knoten, für den gesiebt wird, entlang großer Nachkommen nach unten gehen. Ein Haufen Binärdateien - das heißt, wir haben einen linken und einen rechten Nachkommen. Wir gehen runter zu dem Ast, wo der Nachkomme größer ist. Zu diesem Zeitpunkt findet die Hauptanzahl der Vergleiche statt - die linken / rechten Nachkommen werden miteinander verglichen.







Nachdem wir das Blatt auf der letzten Ebene erreicht hatten, entschieden wir uns für den Zweig, dessen Werte nach oben verschoben werden müssen. Sie müssen jedoch nicht den gesamten Zweig verschieben, sondern nur den Teil, der größer ist als die Wurzel, von der aus Sie begonnen haben.



Daher gehen wir den Zweig hinauf zum nächsten Knoten, der größer als die Wurzel ist.







Der letzte Schritt - Mit der Puffervariablen verschieben wir die Werte der Knoten in der Verzweigung nach oben.







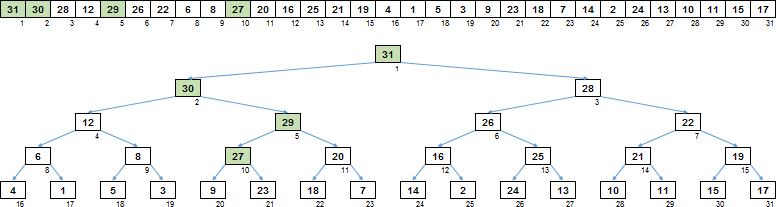
Das ist es. Die aufsteigende Lichtung hat einen Sortierbaum aus einem Array gebildet, in dem jedes Elternteil größer ist als seine Nachkommen.



Letzte Animation:

Python-Implementierung 3.7

Der grundlegende Sortieralgorithmus unterscheidet sich nicht vom regulären Heapsort:

#    
def HeapSortBottomUp(data):

    #    
    #   -   
    # (   )       
    for start in range((len(data) - 2) // 2, -1, -1):
        HeapSortBottomUp_Sift(data, start, len(data) - 1) 

    #        
    #        .
    for end in range(len(data) - 1, 0, -1): 
        #       
        #    
        data[end], data[0] = data[0], data[end]
        #        
        #   
        #     
        HeapSortBottomUp_Sift(data, 0, end - 1)
    return data

Der Abstieg zum unteren Blatt kann bequem / visuell in einer separaten Funktion erfolgen:

#      
#   
def HeapSortBottomUp_LeafSearch(data, start, end):
    
    current = start
    
    #  ,  
    #  (  ) 
    while True:
        child = current * 2 + 1 #  
        #  ,    
        if child + 1 > end: 
            break 
        #  ,   
        if data[child + 1] > data[child]:
            current = child + 1
        else:
            current = child
    
    #  ,    
    child = current * 2 + 1 #  
    if child <= end:
        current = child
        
    return current

Und vor allem - eine Lichtung, die zuerst hinuntergeht, dann auftaucht:

#  
def HeapSortBottomUp_Sift(data, start, end):
    
    #        
    current = HeapSortBottomUp_LeafSearch(data, start, end)
    
    #  ,    
    #     
    while data[start] > data[current]:
        current = (current - 1) // 2
    
    #   ,
    #      
    temp = data[current]
    data[current] = data[start]
    
    #        
    # -     
    while current > start:
        current = (current - 1) // 2
        temp, data[current] = data[current], temp  

Rein empirisch - nach meinen Messungen ist die aufsteigende Heap-Sortierung 1,5-mal schneller als die reguläre Heap-Sortierung.



Nach einigen Informationen (auf der Seite des Algorithmus in Wikipedia, im PDF im Abschnitt "Links") ist BottomUp HeapSort im Durchschnitt sogar einer schnellen Sortierung voraus - für ziemlich große Arrays mit 16.000 Elementen oder mehr.

Verweise

Bottom-up-Heapsort



Eine Variante von Heapsort mit nahezu optimaler Anzahl von Vergleichen



Aufbau von Heaps schnell



Eine neue Variante von Heapsort schlägt im Durchschnitt QuickSort (wenn n nicht sehr klein ist)

Serienartikel:

• Excel-Anwendung AlgoLab.xlsm
• Austausch sortieren
• Einfügungssortierungen
• Nach Auswahl sortieren
  • Haufenarten: n-ary Pyramiden
  • Heap Sorts: Leonardo Numbers
  • Heap Sorts: Schwacher Haufen
  • Bündelsorten: Kartesischer Baum
  • Heap Sorts: Turnierbaum
  • Heap Sort: Rising Sifter
• Sortierungen zusammenführen
• Verteilungssortierung
• Hybridsortierung

Die heutige Sortierung wurde der AlgoLab-Anwendung hinzugefügt, die sie verwendet. Aktualisieren Sie die Excel-Datei mit Makros.