FAISS: Suchen Sie schnell nach Gesichtern und Klonen für Daten im Wert von mehreren Millionen Dollar

Einmal, am Vorabend einer Kundenkonferenz, die jährlich von der DAN-Gruppe abgehalten wurde , haben wir darüber nachgedacht, dass interessante Dinge durchdacht werden könnten, damit unsere Partner und Kunden angenehme Eindrücke und Erinnerungen an die Veranstaltung haben. Wir haben uns entschlossen, ein Archiv mit Tausenden von Fotos von dieser Konferenz und mehreren früheren (zu diesem Zeitpunkt waren es 18) zu analysieren: Eine Person sendet uns sein Foto, und in wenigen Sekunden senden wir ihm eine Auswahl von Fotos aus unseren Archiven für mehrere Jahre.



Wir haben kein Fahrrad erfunden, wir haben die bekannte dlib-Bibliothek genommen und Einbettungen (Vektordarstellungen) jeder Person erhalten. 



Wir haben der Einfachheit halber einen Telegramm-Bot hinzugefügt, und alles war in Ordnung. Unter dem Gesichtspunkt der Gesichtserkennungsalgorithmen funktionierte alles mit einem Knall, aber die Konferenz endete und ich wollte mich nicht von bewährten Technologien trennen. Von mehreren tausend Menschen wollte ich zu Hunderten von Millionen gehen, aber wir hatten keine spezifische Geschäftsaufgabe. Nach einer Weile hatten unsere Kollegen eine Aufgabe, bei der mit so großen Datenmengen gearbeitet werden musste.



Die Frage war, ein intelligentes Bot-Überwachungssystem auf Instagram zu schreiben. Hier führte unser Gedanke zu einem einfachen und komplexen Ansatz: Der



einfache Weg: Betrachten Sie alle Konten, die viel mehr Abonnements als Abonnenten haben, keine Avatare, der vollständige Name ist nicht ausgefüllt usw. Infolgedessen erhalten wir eine unverständliche Menge von halb toten Konten.



Der harte Weg: Da moderne Bots viel schlauer geworden sind und jetzt Posts posten, schlafen und sogar Inhalte schreiben, stellt sich die Frage: Wie können diese gefangen werden? Behalten Sie zuerst ihre Freunde im Auge, da sie oft auch Bots sind, und behalten Sie doppelte Fotos im Auge. Zweitens kann selten ein Bot seine eigenen Bilder erzeugen (obwohl dies möglich ist), was bedeutet, dass doppelte Fotos von Personen in verschiedenen Konten auf Instagram ein guter Auslöser für die Suche nach einem Netzwerk von Bots sind.

Was weiter?

Wenn ein einfacher Pfad ziemlich vorhersehbar ist und schnell zu Ergebnissen führt, ist ein schwieriger Pfad gerade deshalb schwierig, weil wir unglaublich große Mengen an Fotos für nachfolgende Vergleiche von Ähnlichkeiten - Millionen und sogar Milliarden - vektorisieren und indizieren müssen, um ihn zu implementieren. Wie kann man es in die Praxis umsetzen? Immerhin stellen sich technische Fragen:

1. Suchgeschwindigkeit und Genauigkeit
2. Von Daten verwendeter Speicherplatz
3. Die Größe des verwendeten RAM-Speichers. 

Wenn es nur wenige Fotos gäbe, mindestens nicht mehr als zehntausend, könnten wir uns auf einfache Lösungen mit Vektorclustering beschränken. Um jedoch mit großen Vektorvolumina zu arbeiten und die nächsten Nachbarn zu einem bestimmten Vektor zu finden, sind komplexe und optimierte Algorithmen erforderlich.



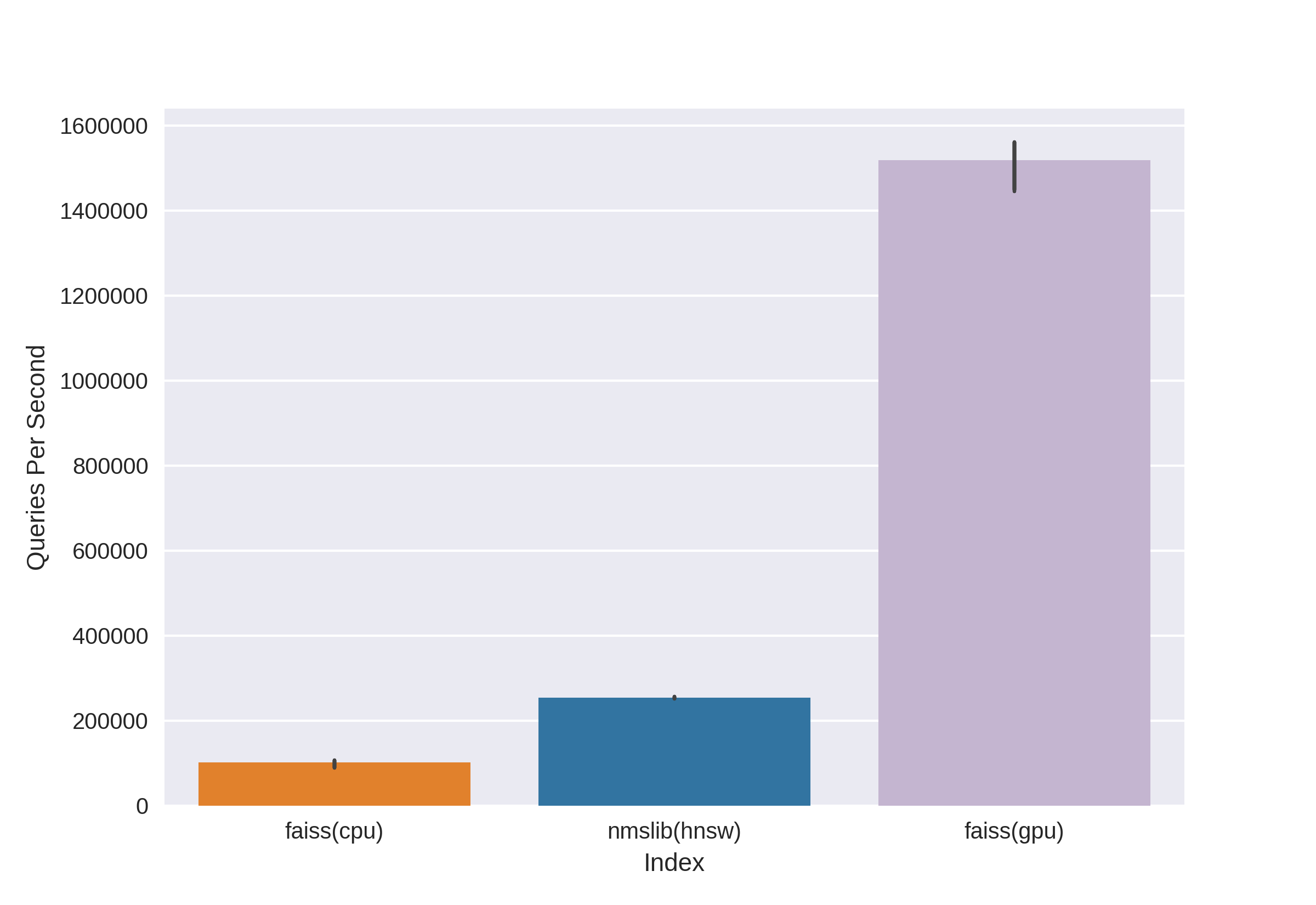
Es gibt bekannte und bewährte Technologien wie Annoy, FAISS, HNSW. Der schnelle HNSW- Nachbarsuchalgorithmus, der in den Bibliotheken nmslib und hnswlib verfügbar istzeigt die neuesten Ergebnisse auf der CPU, wie aus denselben Benchmarks hervorgeht. Wir haben es jedoch sofort abgeschnitten, da wir mit der Menge an Speicher, die bei der Arbeit mit wirklich großen Datenmengen verwendet wird, nicht zufrieden sind. Wir haben uns zwischen Annoy und FAISS entschieden und uns schließlich für FAISS entschieden, weil es bequemer ist, weniger Speicher belegt, möglicherweise auf GPUs verwendet wird und Leistungsbenchmarks verwendet werden (siehe hier ). In FAISS ist der HNSW-Algorithmus übrigens optional implementiert.

Was ist FAISS?

Facebook AI Research Similarity Search ist eine Entwicklung des Facebook AI Research-Teams, mit dem Nachbarn in der Nähe schnell gefunden und im Vektorraum gruppiert werden können. Die hohe Suchgeschwindigkeit ermöglicht das Arbeiten mit sehr großen Datenmengen - bis zu mehreren Milliarden Vektoren.



Der Hauptvorteil von FAISS sind die neuesten Ergebnisse auf der GPU, während die Implementierung auf der CPU hnsw (nmslib) etwas unterlegen ist. Wir wollten sowohl die CPU als auch die GPU durchsuchen können. Darüber hinaus ist FAISS hinsichtlich Speichernutzung und Suche in großen Chargen optimiert.



Mit Source



FAISS können Sie schnell nach den k nächsten Vektoren für einen bestimmten Vektor x suchen. Aber wie funktioniert diese Suche unter der Haube?

Indizes

Das Hauptkonzept in FAISS ist der Index , und im Wesentlichen handelt es sich nur um eine Sammlung von Parametern und Vektoren. Die Parametersätze sind völlig unterschiedlich und hängen von den Bedürfnissen des Benutzers ab. Vektoren können unverändert bleiben oder neu angeordnet werden. Einige Indizes stehen unmittelbar nach dem Hinzufügen von Vektoren zur Arbeit zur Verfügung, andere erfordern eine vorherige Schulung. Vektornamen werden im Index gespeichert: entweder in der Nummerierung von 0 bis n oder als Nummer, die in den Int64-Typ passt.



Der erste und einfachste Index, den wir auf der Konferenz verwendet haben, ist Flat . Es werden nur alle Vektoren in sich selbst gespeichert, und die Suche nach einem bestimmten Vektor wird durch eine umfassende Suche durchgeführt, sodass keine Notwendigkeit besteht, ihn zu trainieren (mehr zum Training weiter unten). Mit einer kleinen Datenmenge kann ein so einfacher Index die Anforderungen der Suche vollständig abdecken.



Beispiel:

import numpy as np
dim = 512  #     512
nb = 10000  #    
nq = 5 #      
np.random.seed(228)
vectors = np.random.random((nb, dim)).astype('float32')
query = np.random.random((nq, dim)).astype('float32')

Erstellen Sie einen Flat-Index und fügen Sie Vektoren ohne Training hinzu:

import faiss
index = faiss.IndexFlatL2(dim)
print(index.ntotal)  #   
index.add(vectors)
print(index.ntotal)  #    10 000 

Jetzt finden wir 7 nächste Nachbarn für die ersten fünf Vektoren aus Vektoren:

topn = 7
D, I = index.search(vectors[:5], topn)  #  : Distances, Indices
print(I)
print(D)

Wir sehen, dass die nächsten Nachbarn mit einem Abstand von 0 die Vektoren selbst sind, der Rest wird durch zunehmenden Abstand angeordnet. Lassen Sie uns unsere Vektoren anhand der Abfrage durchsuchen:

D, I = index.search(query, topn) 
print(I)
print(D)

Jetzt sind die Abstände in der ersten Spalte der Ergebnisse nicht Null, da die Vektoren aus der Abfrage nicht im Index enthalten sind.



Der Index kann auf der Festplatte gespeichert und dann von der Festplatte geladen werden:

faiss.write_index(index, "flat.index")
index = faiss.read_index("flat.index")

Es scheint, dass alles elementar ist! Ein paar Codezeilen - und wir haben bereits eine Struktur für die Suche nach Vektoren mit hoher Dimension. Ein solcher Index mit nur zehn Millionen Vektoren der Dimension 512 wiegt jedoch etwa 20 GB und beansprucht bei Verwendung dieselbe Menge an RAM.



Im Projekt für die Konferenz haben wir einen so grundlegenden Ansatz mit einem flachen Index verwendet. Dank der relativ geringen Datenmenge war alles wunderbar, aber jetzt sprechen wir über Dutzende und Hunderte Millionen hochdimensionaler Vektoren!

Beschleunigen Sie die Suche mit invertierten Listen

Quelle



Das wichtigste und coolste Merkmal von FAISS ist der IVF-Index oder der Inverted File- Index. Die Idee der invertierten Dateien ist lakonisch und wird an den Fingern wunderschön erklärt :



Stellen wir uns eine gigantische Armee vor, die aus den buntesten Kriegern besteht und beispielsweise 1.000.000 Menschen zählt. Es wird unmöglich sein, die gesamte Armee auf einmal zu befehligen. Wie in militärischen Angelegenheiten üblich, ist es notwendig, unsere Armee in Einheiten aufzuteilen. Teilen wir durch$$$\sqrt{1 000 000} = 1000$ungefähr gleiche Teile, für die Rolle der Kommandeure einen Vertreter aus jeder Einheit wählen. Und wir werden versuchen, so ähnlich wie möglich in Charakter, Herkunft, physischen Daten usw. zu senden. Soldaten in einer Einheit, und wir wählen den Kommandanten so aus, dass er seine Einheit so genau wie möglich darstellt - er war jemand "Durchschnitt". Infolgedessen wurde unsere Aufgabe vom Kommando einer Million Soldaten auf das Kommando der 1000. Einheiten durch ihre Kommandeure reduziert, und wir haben eine ausgezeichnete Vorstellung von der Zusammensetzung unserer Armee, da wir wissen, was Kommandeure sind.



Dies ist die Idee hinter dem IVF-Index: Gruppieren wir eine große Menge von Vektoren Stück für Stück unter Verwendung des k-means- AlgorithmusEin Vektor, der jedem Teil einen Schwerpunkt entspricht, ist ein Vektor, der das ausgewählte Zentrum für einen bestimmten Cluster ist. Die Suche wird über den Mindestabstand zum Schwerpunkt durchgeführt, und erst dann werden wir nach den Mindestabständen zwischen den Vektoren im Cluster suchen, die dem angegebenen Schwerpunkt entsprechen. K gleich nehmen$$$\sqrt{n}$wo $$$n$ - Mit der Anzahl der Vektoren im Index erhalten wir die optimale Suche auf zwei Ebenen - zuerst unter $$$\sqrt{n}$ Schwerpunkt dann unter $$$\sqrt{n}$Vektoren in jedem Cluster. Die Suche wird im Vergleich zur umfassenden Suche mehrmals beschleunigt, was eines unserer Probleme bei der Arbeit mit vielen Millionen Vektoren löst.





Der Vektorraum wird nach der k-means-Methode in k Cluster unterteilt. Jedem Cluster ist ein Schwerpunkt zugeordnet.



Beispielcode:

dim = 512
k = 1000  #  “”
quantiser = faiss.IndexFlatL2(dim) 
index = faiss.IndexIVFFlat(quantiser, dim, k)
vectors = np.random.random((1000000, dim)).astype('float32')  # 1 000 000 “”

Oder Sie können es viel eleganter aufschreiben, indem Sie das praktische FAISS-Ding zum Erstellen eines Index verwenden:

index = faiss.index_factory(dim, “IVF1000,Flat”)
 :
print(index.is_trained)   # False.
index.train(vectors)  # Train    
 
#  ,      ,      :
print(index.is_trained)  # True
print(index.ntotal)   # 0
index.add(vectors)
print(index.ntotal)   # 1000000

Nachdem wir diese Art von Index nach Flat untersucht haben, haben wir eines unserer potenziellen Probleme gelöst - die Suchgeschwindigkeit, die im Vergleich zur vollständigen Suche um ein Vielfaches niedriger wird.

D, I = index.search(query, topn) 
print(I)
print(D)

Es gibt jedoch ein "aber" - die Genauigkeit der Suche sowie die Geschwindigkeit hängen von der Anzahl der besuchten Cluster ab, die mit dem Parameter nprobe festgelegt werden können:

print(index.nprobe)  # 1 –           
index.nprobe = 16  #   -16    top-n  
D, I = index.search(query, topn) 
print(I)
print(D)

Wie Sie sehen können, haben wir nach dem Erhöhen von nprobe völlig unterschiedliche Ergebnisse. Die Spitze der kürzesten Entfernungen in D ist besser geworden.



Sie können nprobe gleich der Anzahl der Schwerpunkte im Index nehmen, dann entspricht dies einer Brute-Force-Suche, die Genauigkeit ist am höchsten, aber die Suchgeschwindigkeit nimmt merklich ab.

Durchsuchen der Festplatte - In Festplatten invertierte Listen

Nun, wir haben das erste Problem gelöst. Jetzt erhalten wir auf zig Millionen Vektoren eine akzeptable Suchgeschwindigkeit! Aber all dies ist nutzlos, solange unser riesiger Index nicht in den Arbeitsspeicher passt.



Speziell für unsere Aufgabe ist der Hauptvorteil von FAISS die Möglichkeit, IVF-Indizes für invertierte Listen auf der Festplatte zu speichern und nur Metadaten in den Arbeitsspeicher zu laden.



Wie erstellen wir einen solchen Index: Wir trainieren indexIVF mit den erforderlichen Parametern für die maximal mögliche Datenmenge, die in den Speicher passt, fügen dann Vektoren (die trainiert wurden und nicht nur) zum trainierten Index in Teilen hinzu und schreiben den Index für jedes der Teile auf die Festplatte.

index = faiss.index_factory(512, “,IVF65536, Flat”, faiss.METRIC_L2)

Das GPU-Index-Training wird folgendermaßen durchgeführt:

res = faiss.StandardGpuResources()
index_ivf = faiss.extract_index_ivf(index)
index_flat = faiss.IndexFlatL2(512)
clustering_index = faiss.index_cpu_to_gpu(res, 0, index_flat)  #  0 –  GPU
index_ivf.clustering_index = clustering_index

faiss.index_cpu_to_gpu (res, 0, index_flat) kann durch faiss.index_cpu_to_all_gpus (index_flat) ersetzt werden , um alle GPUs zusammen zu verwenden.



Es ist sehr wünschenswert, dass die Trainingsstichprobe so repräsentativ wie möglich ist und eine gleichmäßige Verteilung aufweist. Daher setzen wir den Trainingsdatensatz aus der erforderlichen Anzahl von Vektoren vor und wählen sie zufällig aus dem gesamten Datensatz aus.

train_vectors = ...  #     
index.train(train_vectors)

#    ,   :
faiss.write_index(index, "trained_block.index") 

#       
#      :
for bno in range(first_block, last_block+ 1):
    block_vectors = vectors_parts[bno]
    block_vectors_ids = vectors_parts_ids[bno]  # id ,  
    index = faiss.read_index("trained_block.index")
    index.add_with_ids(block_vectors, block_vectors_ids)
    faiss.write_index(index, "block_{}.index".format(bno))

Danach vereinen wir alle invertierten Listen. Dies ist möglich, da jeder der Blöcke tatsächlich der gleiche trainierte Index ist, nur mit unterschiedlichen Vektoren im Inneren.

ivfs = []
for bno in range(first_block, last_block+ 1):
    index = faiss.read_index("block_{}.index".format(bno), faiss.IO_FLAG_MMAP)
    ivfs.append(index.invlists)
    #  index   inv_lists 
    #        :
    index.own_invlists = False

#   :
index = faiss.read_index("trained_block.index")

#   invlists
#  invlists       merged_index.ivfdata
invlists = faiss.OnDiskInvertedLists(index.nlist, index.code_size, "merged_index.ivfdata")
ivf_vector = faiss.InvertedListsPtrVector() 

for ivf in ivfs: 
    ivf_vector.push_back(ivf)

ntotal = invlists.merge_from(ivf_vector.data(), ivf_vector.size())
index.ntotal = ntotal  #     
index.replace_invlists(invlists)  
faiss.write_index(index, data_path + "populated.index")  #    

Fazit : Jetzt ist unser Index populated.index und fusioned_blocks.ivfdata Dateien .



Der populated.index enthält den ursprünglichen vollständigen Pfad zur Datei mit invertierten Listen. Wenn sich also der Pfad zur ivfdata-Datei aus irgendeinem Grund ändert, müssen Sie beim Lesen des Index das Flag faiss.IO_FLAG_ONDISK_SAME_DIR verwenden , mit dem Sie im selben Verzeichnis wie nach der ivfdata-Datei suchen können populated.index:

index = faiss.read_index('populated.index', faiss.IO_FLAG_ONDISK_SAME_DIR)

Als Grundlage diente das Demo-Beispiel aus dem Github FAISS-Projekt .



Eine Kurzanleitung zur Auswahl eines Index finden Sie im FAISS Wiki . Zum Beispiel konnten wir einen Trainingsdatensatz von 12 Millionen Vektoren in den RAM einpassen, also haben wir den IVFFlat-Index für 262144 Zentroide gewählt, um ihn dann auf Hunderte von Millionen zu skalieren. Es wird auch vorgeschlagen, den Index IVF262144_HNSW32 in der Anleitung zu verwenden, in dem die Zugehörigkeit eines Vektors zu einem Cluster durch den HNSW-Algorithmus mit 32 nächsten Nachbarn bestimmt wird (mit anderen Worten, unter Verwendung des Quantisierers IndexHNSWFlat), aber wie es uns in weiteren Tests erschien, ist die Suche nach einem solchen Index weniger genau. Darüber hinaus sollte berücksichtigt werden, dass ein solcher Quantisierer die Möglichkeit der Verwendung auf der GPU ausschließt.

Reduzieren Sie die Festplattennutzung durch Produktquantisierung drastisch

Dank der Festplattensuchmethode war es möglich, die Last aus dem RAM zu entfernen, aber ein Index mit einer Million Vektoren benötigte immer noch etwa 2 GB Festplattenspeicher, und wir sprechen über die Möglichkeit, mit Milliarden von Vektoren zu arbeiten, die mehr als zwei TB erfordern würden! Natürlich ist das Volumen nicht so groß, wenn Sie sich ein Ziel setzen und zusätzlichen Speicherplatz zuweisen, aber es hat uns ein wenig gestört.



Und hier kommt die Vektorkodierung zur Rettung, nämlich die Skalarquantisierung (SQ) und die Produktquantisierung (PQ).... SQ - Codierung jeder Komponente des Vektors in n Bits (normalerweise 8, 6 oder 4 Bits). Wir werden die PQ-Option in Betracht ziehen, da die Idee, eine float32-Komponente mit acht Bits zu codieren, hinsichtlich des Genauigkeitsverlusts zu deprimierend erscheint. Obwohl in einigen Fällen die Komprimierung von SQfp16 auf float16 nahezu verlustfrei ist.



Das Wesen der Produktquantisierung ist wie folgt: Vektoren der Dimension 512 sind in n Teile unterteilt, von denen jeder in 256 mögliche Cluster (1 Byte) gruppiert ist, d.h. Wir stellen einen Vektor mit n Bytes dar, wobei n in einer FAISS-Implementierung normalerweise höchstens 64 ist. Eine solche Quantisierung wird jedoch nicht auf die Vektoren aus dem Datensatz selbst angewendet, sondern auf die Unterschiede dieser Vektoren und der entsprechenden Schwerpunkte, die in der Erzeugungsstufe der invertierten Listen erhalten wurden! Es stellt sich heraus, dass invertierte Listen Sätze von Abständen zwischen Vektoren und ihren Schwerpunkten codiert werden.

index = faiss.index_factory(dim, "IVF262144,PQ64", faiss.METRIC_L2)

Es stellt sich heraus, dass wir jetzt nicht alle Vektoren speichern müssen - es reicht aus, n Bytes pro Vektor und 2048 Bytes pro Schwerpunktvektor zuzuweisen. In unserem Fall haben wir genommen$$$n = 64$, also $$$\frac{512}{64} = 8$- Länge eines Teilvektors, der in einem von 256 Clustern definiert ist.







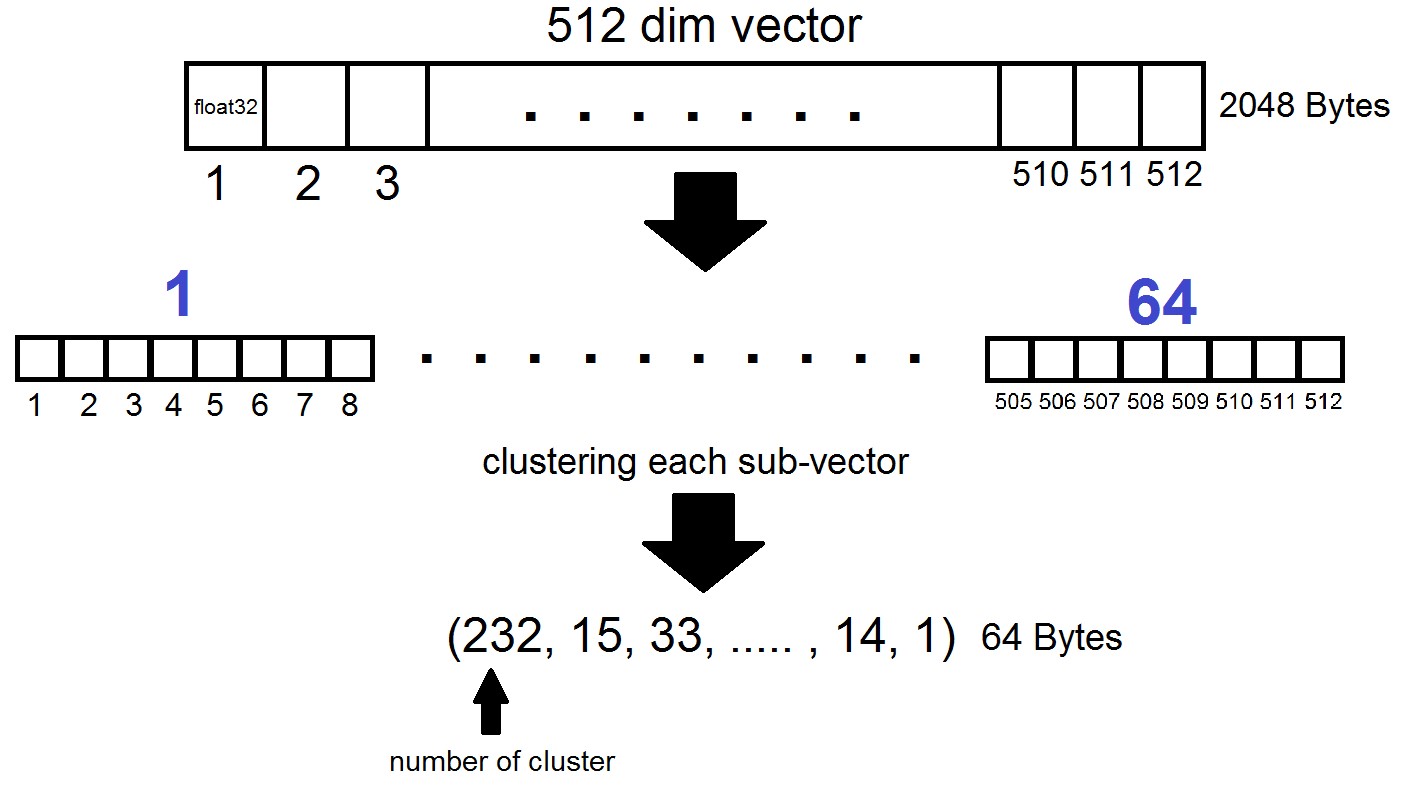
Bei der Suche nach dem Vektor x werden die nächsten Zentroide zuerst mit dem üblichen flachen Quantisierer bestimmt, und dann wird x auch in Untervektoren unterteilt, von denen jeder durch die Nummer eines der 256 entsprechenden Zentroide codiert ist. Und der Abstand zum Vektor ist definiert als die Summe von 64 Abständen zwischen den Untervektoren.

Was ist das Ergebnis?

Wir haben unsere Experimente mit dem Index "IVF262144, PQ64" abgebrochen, da er alle unsere Anforderungen hinsichtlich Suchgeschwindigkeit und -genauigkeit vollständig erfüllte und auch bei der weiteren Skalierung des Index eine angemessene Nutzung des Speicherplatzes sicherstellte. Insbesondere belegt der Index derzeit mit 315 Millionen Vektoren 22 GB Speicherplatz und bei Verwendung etwa 3 GB RAM.



Ein weiteres interessantes Detail, das wir zuvor nicht erwähnt haben, ist die vom Index verwendete Metrik. Standardmäßig werden die Abstände zwischen zwei beliebigen Vektoren in der euklidischen L2-Metrik berechnet, oder in einer verständlicheren Sprache werden die Abstände als Quadratwurzel der Summe der Quadrate der koordinatenweisen Differenzen berechnet. Sie können jedoch auch eine andere Metrik angeben. Insbesondere haben wir die Metrik METRIC_INNER_PRODUCT getestetoder Metrik der Kosinusabstände zwischen Vektoren. Es ist Cosinus, weil der Cosinus des Winkels zwischen zwei Vektoren im euklidischen Koordinatensystem als Verhältnis des skalaren (koordinatenweisen) Produkts von Vektoren zum Produkt ihrer Längen ausgedrückt wird. Wenn alle Vektoren in unserem Raum die Länge 1 haben, ist der Cosinus des Winkels genau gleich dem koordinatenweisen Produkt. In diesem Fall ist ihr Skalarprodukt umso näher an der Einheit, je näher die Vektoren im Raum liegen.



Die Metrik L2 hat einen direkten mathematischen Übergang zur Metrik der Skalarprodukte. Beim experimentellen Vergleich der beiden Metriken hatte man jedoch den Eindruck, dass die Punktproduktmetrik uns hilft, die Ähnlichkeitskoeffizienten von Bildern besser zu analysieren. Zusätzlich wurden die Einbettungen unserer Fotos mit erhaltenInsightFace , das die ArcFace- Architektur mithilfe von Kosinusabständen implementiert . Es gibt auch andere Metriken in FAISS-Indizes, über die Sie hier lesen können .

Fazit und kuriose Beispiele

Also zurück zu dem Punkt, an dem alles begann. Und es begann, wie Sie sich erinnern, mit der Motivation, das Problem der Suche nach Bots im Instagram-Netzwerk zu lösen und insbesondere nach doppelten Posts mit Personen oder Avataren in bestimmten Benutzergruppen zu suchen. Während des Schreibens des Materials wurde klar, dass eine detaillierte Beschreibung unserer Methodik für die Suche nach Bots einen separaten Artikel erfordern würde, den wir in den folgenden Veröffentlichungen diskutieren werden, aber wir werden uns vorerst auf Beispiele unserer Experimente mit FAISS beschränken.



Sie können Bilder oder Gesichter auf verschiedene Arten vektorisieren. Wir haben uns für die InsightFace-Technologie entschieden (das Vektorisieren von Bildern und das Auswählen von n-dimensionalen Merkmalen ist eine separate lange Geschichte). Im Verlauf von Experimenten mit der erhaltenen Infrastruktur wurden interessante und lustige Eigenschaften entdeckt.



Nachdem wir beispielsweise die Erlaubnis von Kollegen und Bekannten eingeholt hatten, haben wir ihre Gesichter in die Suche hochgeladen und schnell Fotos gefunden, auf denen sie vorhanden sind:





Unser Kollege hat ein Foto eines Comic-Con-Besuchers aufgenommen, der sich im Hintergrund in einer Menschenmenge befindet. Quelle





Picknick in einer großen Gesellschaft von Freunden, ein Foto von einem Konto des Freundes. Quelle





Nur vorbei. Ein unbekannter Fotograf hat die Jungs für sein thematisches Profil festgehalten. Sie wussten nicht, wo ihr Foto gelandet war und vergaßen nach 5 Jahren völlig, wie sie fotografiert wurden. Quelle





In diesem Fall ist der Fotograf unbekannt und wird heimlich fotografiert!

Sofort erinnerte sich das verdächtige Mädchen mit SLR, das im Moment vor :) Source saß



Mit FAISS können Sie auf einfache Weise ein Analogon des bekannten FindFace auf Ihrem Knie zusammenstellen.



Ein weiteres interessantes Merkmal: Je mehr Gesichter sich im FAISS-Index ähneln, desto näher sind die entsprechenden Vektoren im Raum beieinander. Ich beschloss, mir die etwas weniger genauen Suchergebnisse in meinem Gesicht genauer anzusehen und fand Klone, die mir schrecklich ähnlich waren :)





Einige der Klone des Autors.





Fotoquellen : 1 , 2 ,  3 Im Allgemeinen eröffnet FAISS ein riesiges Feld für die Umsetzung kreativer Ideen. Zum Beispiel wäre es nach dem gleichen Prinzip der Vektornähe ähnlicher Gesichter möglich, Pfade von einer Person zur anderen zu bauen. Oder machen Sie FAISS als letzten Ausweg zu einer Fabrik für die Herstellung solcher Meme:





Quelle



Vielen Dank für Ihre Aufmerksamkeit und wir hoffen, dass dieses Material für Habr-Leser nützlich sein wird!



Dieser Artikel wurde mit Unterstützung meiner Kollegen Artyom Korolyov (korolevart), Timur Kadyrov und Arina Reshetnikova.



F & E Dentsu Aegis Network Russland.